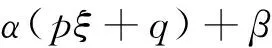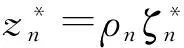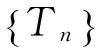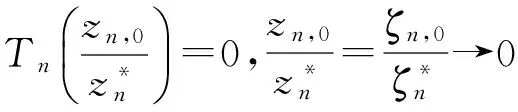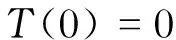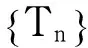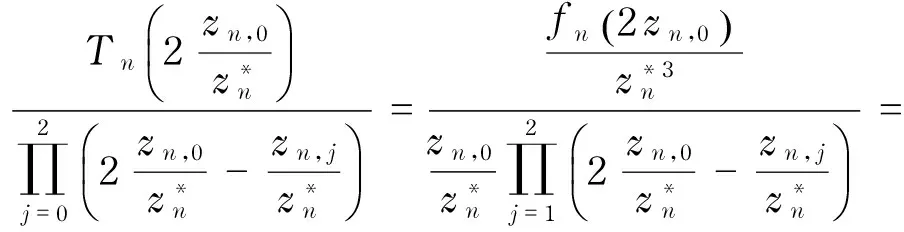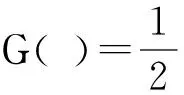零点分布在直线上的亚纯函数的正规定则

洪苏敏,　刘晓俊

(上海理工大学 理学院,上海　200093)



零点分布在直线上的亚纯函数的正规定则

洪苏敏,刘晓俊

(上海理工大学 理学院,上海200093)

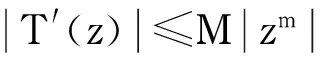
摘要：对零点分布在给定直线上的亚纯函数的正规性进行了讨论,设F是定义在单位圆盘D上的亚纯函数族,若存在M≥0,使得对于任意f∈F满足:f(z)=0⟹;f(z)的零点分布在一条给定直线上;f(z)的极点重数至少为≠zm,则F在区域D上正规.

关键词：亚纯函数; 例外函数; 零点; 正规族

1问题的提出

Bloch[1]曾经提出:相应于每一个Picard型定理,必定存在一个正规定则.

Picard型定理:设P是一个亚纯函数的性质,若复平面上的亚纯函数f在复平面上满足性质P,即〈f,〉∈P,则必有f≡常数.根据Bloch原理,那么对于区域D上的亚纯函数族F,它的每一个元素f在区域D上满足性质P,即〈f,〉∈P,则必在区域D上正规.

1959年,Hayman[2]证明了如下的Picard型定理1,取性质P1={f(z)≠0,f(k)(z)≠1,k∈+}.

定理1设f为复平面上的亚纯函数,若f∈P1,则f≡常数.

1979年,顾永兴[3]证明了对应的正规定则,得到了定理2.

定理2设F为区域D的亚纯函数族,k∈+,若对于任意的f∈F,f∈P1,则F在D内正规.

由此可见,上述性质P1满足Bloch原理.

此后,杨乐[4]、庞学诚等[5-6]、方明亮等[7]、常建明[8]均对上述P1下所得的正规定则作了不同程度的推广.

2013年,童晓丽等[9]首先考虑将“f(z)≠0”减弱为“f(z)的零点分布在一条给定的直线上”,得到了定理3.

定理3设F是定义在单位圆盘D上的亚纯函数族,若存在M≥0,使得对于任意f∈F,满足以下条件,则F在D上正规:

b.f(z)的零点分布在一直线上;

c.f(z)的极点重级m≥3;

d.f′(z)≠1.

2014年,张培[10]将定理3中的条件“f′(z)≠1”改为“f′(z)≠z”,得到定理4.

定理4设F是定义在单位圆盘D上的亚纯函数族,若存在M≥0,使得对于任意f∈F,满足以下条件,则F在D上正规:

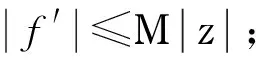
b.f(z)的零点分布在一直线上;

c.f(z)的极点重级m≥3;

d.f′(z)≠z.

本文在上述定理的基础上,将例外函数推广到一般形式zm,得到定理5.

定理5设F是定义在单位圆盘D上的亚纯函数族,若存在M≥0,使得对于任意f∈F,满足以下条件,则F在D上正规:

a.f(z)的零点分布在一直线上;

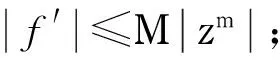
c.f(z)的极点重级l≥3;

d.f′(z)≠zm,这里m∈+.

下面通过一些例子来说明定理5中条件a和c的必要性.

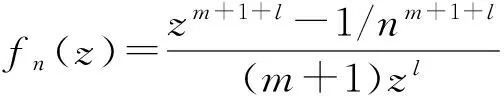
例3取

简单计算得

例4取

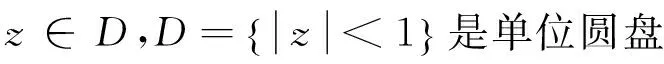
且简单计算可得

当n→时,故显然有fn=0⟹,且这里的M>0可取为任意小.但是,在z=0处不正规.实际上,这个例子是对例2中函数fn的两个不同的重级零点作扰动所得.

例5取

上面的反例中当零点不位于直线时,都位于某个圆心在原点的圆周上,接下来研究是否存在其他情况.

例6取

简单计算得

2相关引理

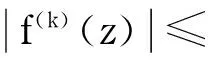
a. 点列zn→z0;

b. 函数列fn∈F;

c. 正数列ρn→0+.

引理2[1]设f在上非常值亚纯,b≠0是复常数,k∈+,则f或f(k)-b有零点;若f为超越亚纯函数,则f或f(k)-b有无穷多个零点.

引理3[12]设f为上有穷级亚纯函数,则对于f的每一个非直接渐近值a,存在zn,使得f(zn)→a,且f′(zn)=0.

引理4[13]设f是上的亚纯函数,其有限临界值集和渐近值集有界,则存在正数r0,使得当>r0和>r0时,有

a.n=k,且n!an=1;

引理6设f是上的非常值有穷级亚纯函数,M>0是常数,f(z)=0⟹,且f′(z)≠zm,则或者,其中是有穷复数,l∈+,或者,其中α(≠0),β是有穷复数.

故由Denjoy-Carelman-Ahlfors的结果,g(z)的直接渐近值≤2ρg个,于是g(z)的有穷临界值和渐近值构成的集合有界.

不妨设R0是它的某个上界,则由引理4得

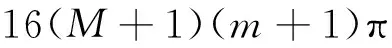
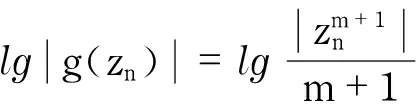
a.f(z)为多项式.

b.f(z)是非多项式有理函数.

因为f′(z)≠zm,所以h′(z)≠1.由引理5,得

则

即得引理6.

3定理5的证明

由定理3,只要证明F在z=0处正规即可.

假设F1在z=0处不正规.

由引理1,存在zn→0,ρn→0+,Fn∈F1,使得

其中,g为非常值有穷级亚纯函数,且满足g#(ζ)≤g#(0)=M+1.

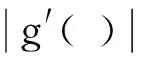
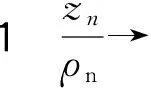
断言g′(ζ)≠1.

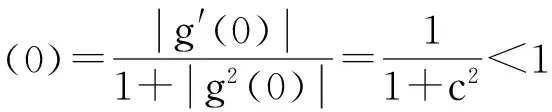
令

显然

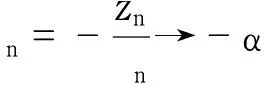
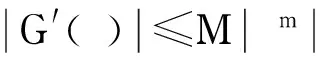
情况2.1G′(ζ)≢ζm.

或

这里a,b≠0,c和α≠0,β都是复常数,l∈+.

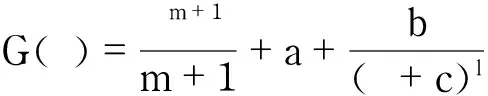
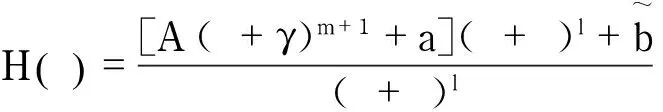
不妨设M1(ξ)的零点分别为t1

另一方面,M1′(ξ)=(ξ+η)l-1[(m+1)·(ξ+γ)m(ξ+η)+l(ξ+γ)m+1+al/A],则-η作为M1′(ξ)的零点只可能是τj中的某个,故其重数只能是1,与l-1≥2矛盾.

于是,H(ξ)不存在,从而这样的G(ζ)亦不存在.

于是,可以假设

再分两种情况讨论.

若存在η>0,使得fn在Δ(0,η)上仅以zn,j=ρnζn,j为零点,则令

但

矛盾.

于是,任意η>0,fn在Δ(0,η)内除zn,j(j=0,1,2)外至少还有一个零点,记为zn,3=ρnζn,3,显然当n→时,ζn,3→.令,易得在*={0}上正规.

若Kn在z=0处正规,则Kn在上正规,记Kn⟹K在上.

故

但由

此时,若fn在Δ(0,δ)上仅有3个非零的零点zn,j=ρnζn,j,j=0,1,2,则在上有

但当n→时,

矛盾.

于是,fn在Δ(0,δ)上至少还有一个零点zn,3=ρnζn,3,ζn,3→,n→.

下面再分3种情况讨论:

情况2.2G′(ζ)≡ζm.

4定理5的相关分析

在定理5的证明过程中,可得

这里b≠0是常数.若此时,G仅有简单极点,则l=1,且

这里

由定理1的条件a可得,H的零点分布在一条直线上.不妨设其在实轴上,即H仅有实零点.因为degH=m+2,所以H有m+2个实零点(计重数).由罗尔定理得,H″有m个实零点(计重数).但H″(ζ)=(m+1)ζm-1[2ζ+m(ζ+c)],其至多仅有两个不同零点.

a. 若c=0,则H″以0为m重零点,故当m≥2时,H至多仅有两个不同零点.设H=(ζ-x0)p·(ζ-x1)q,由于

故x0≠x1.再由p+q=m+2≥4得,p≥2或者q≥2.若p,q≥2,则由罗尔定理得,H″至少有两个不同零点,矛盾.故p,q中至少一个为1,不妨设p=1,q=m+1,则由b≠0得,x1≠0,故H=(ζ-x0)(ζ-x1)m+1,H″(x1)=0,矛盾.更进一步,若m=1,则不妨设

由于b≠0,且xi∈,故a≠0.两边展开比较得,-x0x1x2=2b.再由定理1的条件b得|G′(xi)|≤M|xi|,代入前式得,i.此时,若要求M≤1,则必有xjxk<0,则必存在某个j≠k,使得xj=xk.不妨设x0=x1,再由x0+x1+x2=0得,x2=-2x0≠0,再代入,得,矛盾.

故x0≠x1.再由p+q=m+2≥5得,p≥3或者q≥3.若p,q≥3,则由罗尔定理得,H″至少有3个不同零点,矛盾.故p,q中至少一个为2,不妨设p=2,q=m,则由m≥3得x1≠0,再由罗尔定理得,H″至少有3个不同零点,矛盾.

综上所述,当函数族F仅有简单极点时,其反例应该类似于例3. 同理可得,当F的极点为二重时,其反例也应该类似于例2或者例4.

参考文献：

[1]顾永兴,庞学诚,方明亮.正规族理论及其应用[M].北京:科学出版社,2007.

[2]HAYMAN W K.Meromorphic functions[M].Oxford:Clarendon Press,1964:17-65.

[3]GU Y X.A normal criterion of meromorphic families[J].Scientia Sinica,1979,1:267-274.

[4]YANG L.The normality of meromorphic fuctions[J].Science in China(Series A),1986,29(9):897-908.

[5]PANG X C,YANG D G,ZALCMAN L.Normal families of meromorphic functions whose derivatives omit a function[J].Computational Methods and Function Theory,2003,2(1):257-265.

[6]PANG X C,ZALCMAN L.Normal families of meromorphic functions with multiple zeros and poles[J].Israel Journal of Mathematics,2003,136(1):1-9.

[7]WANG Y F,FANG M L.Picard values and normal families of meromorphic functions with multiple zeros[J].Acta Mathematica Sinica,English Series,1998,14(1):17-26.

[8]CHANG J M.Normality and quasinormality of zero-free meromorphic functions[J].Acta Mathematica Sinica,English Series,2012,28(4):707-716.

[9]童晓丽,刘晓俊.零点位于直线上的亚纯函数的正规定则[J].上海理工大学学报,2014,36(4):362-365.

[10]张培.涉及零点分布的亚纯函数的正规定则[D].上海:上海理工大学,2014.

[11]PANG X C,ZALCMAN L.Normal families and shared values[J].Bulletin of the London Mathematical Society,2000,32(3):325-331.

[12]BERGWEILER W,EREMENKO A.On the singularities of the inverse to a meromorphic function of finite order[J].Revista Matematica Iberoamericana,1995,11(2):355-373.[13]BERGWEILER W.On the zeros of certain homogeneous differential polynomials[J].Archiv der Mathematik,1995,64(3):192-202.

(编辑:丁红艺)

Normal Criterion of Meromorphic Functions Whose Zeros Distribute on a Certain Straight

LineHONG Sumin,LIU Xiaojun

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：The normality of meromorphic functions whose zeros distribute on a certain straight lines was discussed and obtained:let F be a family of meromorphic functions on the unit disc D,if there exists M≥0,such that for each f∈F,f(z)=0⟹,all zeros of f(z) distribute on a certain straight line,all of whose poles have multiplicity at least 3,and ≠zm,z∈D,then F is normal on D.

Keywords：meromorphic functions; exceptional function; zeros; normal family

文章编号：1007-6735(2016)03-0211-07

DOI：10.13255/j.cnki.jusst.2016.03.002

收稿日期：2015-09-18

基金项目：国家自然科学基金青年基金资助项目(11401381)

通信作者：刘晓俊(1982-),男,副教授.研究方向:复分析.E-mail:xiaojunliu2007@hotmail.com

中图分类号：O 174.52

文献标志码：A

第一作者： 洪苏敏(1992-),女,硕士研究生.研究方向:复分析.E-mail:hongsuminyun@163.com