用导数求曲线经过一点切线的讨论
吴邦昆
(合肥职业技术学院,安徽 合肥 238000)
用导数求曲线经过一点切线的讨论
吴邦昆
(合肥职业技术学院,安徽 合肥 238000)
摘 要:利用导数求曲线经过一点的切线方程,由于所经过的这一点位置、角色的不同,求切线方程的方法往往不一样,这里就经过的这一点在不在曲线上,曲线在该点是否可导,所求切线是否唯一这几个方面,对利用导数求曲线经过一点的切线问题进行讨论。
关键词:导数;曲线;切线;讨论
利用导数求曲线经过一点的切线方程,需要具体分析该点是否在曲线上,若该点在曲线上,曲线在该点是否可导,该点是否为切点以及所求切线是否唯一。不同情行需要采取不同方法,只有这样才能使解题过程严谨而周密,不会出现这样或那样的问题。初学者在解决这类问题时往往忽视分析,习惯直接利用导数的几何意义求切线方程,这样经常会出现似是而非的结果。下面就不同情行下,对利用导数求曲线经过一点的切线方程问题进行讨论。
问题一、点不在曲线上
求切线方程的一般解决方法如下:
问题二、点在曲线上,但曲线在该点不可导
情形1:曲线在该点不可导,曲线过该点的切线不存在。
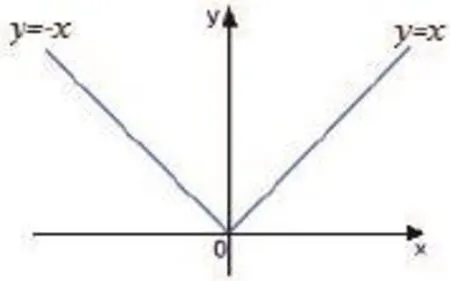

情形2:曲线在该点不可导,曲线过该点的切线存在。
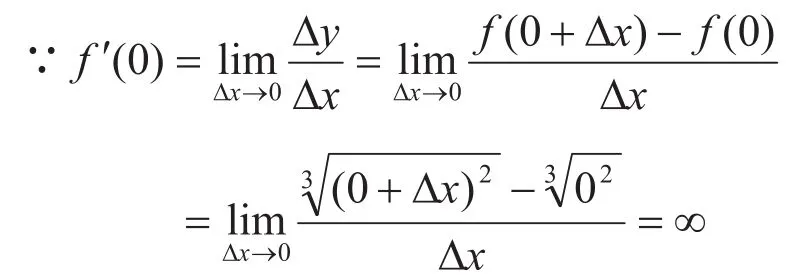
问题三、点在曲线上,曲线在该点可导
⑦ 刘译:What makes the difference is that one has heard the Way before the other and that one is more specialized in his craft and trade than the other-that is all.[4]38
分析:点(1,1)显然在此曲线上,且曲线在此点可导,求曲线在点(1,1)处的切线方程,则说明点(1,1)是所求切线的切点,可直接利用导数的几何意义求解。
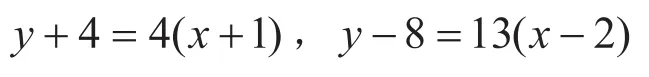
利用导数求曲线经过一点的切线方程,要根据实际问题进行具体分析,不同情行需要采取不同方法,只有这样才能使解题过程严谨而周密,不会出现这样或那样的问题。
参考文献:
[1]殷瑕.例谈利用导数求解曲线的切线问题[J].中学课程辅导(教学研究),2013,(3).
[2]李亚章.导数在研究切线问题中的应用举例[J].中学数学月刊,2012,(3).
[3]桑观赏.用导数求切线方程的四种类型[J].中学生数理化(高二版),2012,(1).
[4]郭奕俊.求曲线切线应注意的一个问题[J].中学数学研究,2012,(9).
[5]同济大学应用数学系主编.高等数学(上册)[M].北京:高等教育出版社,2002.
(责任编辑:韩拥军)
中图分类号:O182
文献标识码:A
文章编号:1671-752X(2016)02-0072-02
收稿日期:2015-12-27
作者简介:吴邦昆(1964-),男,安徽庐江人,合肥职业技术学院副教授,研究方向:高等数学教育教学。
基金项目:安徽高校省级质量工程项目“《高等数学》精品资源共享课程”(编号:2013gxk161);合肥职业技术学院质量工程项目“《高等数学》精品课程”(编号:JPKC201302)。

