基于块稀疏贝叶斯学习算法的心电数据重构

陈少峰 CHEN Shaofeng徐文龙 XU Wenlong



基于块稀疏贝叶斯学习算法的心电数据重构

陈少峰 CHEN Shaofeng
徐文龙 XU Wenlong

College of Information Engineering, China Jiliang University, Hangzhou 310018, China

Address Correspondence to： CHEN Shaofeng E-mail： 913279957@qq.com

修回日期：2015-12-03

中国医学影像学杂志

2016年 第24卷 第3期：223-226

Chinese Journal of Medical Imaging 2016 Volume 24 （3）： 223-226

【摘要】压缩感知（CS）技术在心电信号上的应用具有低成本、低功耗等优势，但传统的CS算法重构心电信号质量并不理想。本文介绍了一种基于信号块结构内相关性的块稀疏贝叶斯学习（BSBL）CS算法；并对MIT-BIH数据库中心电数据进行实验结果显示其均方根误差远低于传统CS算法，表明该算法能够高质量重构心电信号BSBL算法在心电数据上的应用有效降低了对数据的采样频率，从而缓解存储压力并降低功耗。

【关键词】信号处理，计算机辅助；压缩感知；算法；块稀疏贝叶斯学习

根据世界卫生组织于2014年5月更新的有关全球疾病状况的评估报告显示，在过去10年中，缺血性心脏病、脑卒中、下呼吸道感染和慢性阻塞性肺疾病是导致人类死亡的4大主要原因，其中缺血性心脏病是导致全球范围人口死亡的第一因素。心电信号是诊断心血管疾病的主要依据，因此快速、准确检测患者心电活动具有重要的意义。

2006年，Candes等［1］提出的压缩感知（compressed sensing，CS）理论。由于其突破了传统奈奎斯特（Nyquist）采样定理的瓶颈，能够通过非确定线性系统稀疏求解，从远少于Nyquist采样频率的采样点中几乎无失真的恢复信号。CS在信号采集和数据处理上具有突出的优势，将其引入心电数据中可以减少对存储空间、数据传输量和信道传输带宽的需求，因而可以大幅度降低存储和传输数据的费用。Mamaghanian等［2］给出了小波基下心电信号在BSNs节点上的CS框架，并通过凸优化方法求解Basic Pursuit De-Noising问题实现心电信号的重构。Dixon等［3］讨论了时域阈值稀疏化后心电信号的CS，并实现16倍压缩因子的心电信号压缩。Mamaghanian和Dixon等的研究着重讨论了CS在心电监护中的应用框架，但是对非稀疏心电信号重构算法没有深入讨论。Zhang等［4］研究了块稀疏信号的块内相关性，提出了块稀疏贝叶斯学习（block spare bayesian learning，BSBL）［5］算法，并成功将该算法应用到非稀疏的胎儿心电信号中。BSBL是目前已知算法中唯一能够在高压缩率下高质量恢复非稀疏心电信号的CS重构算法。

为实现非稀疏心电信号快速精确重构，本文将在BSBL框架下对在MIT-BIH数据库上的心电信号测试以均方根误差（root mean square error，RMSE）评价重构效果，旨在检验BSBL算法是否能实现非稀疏信号的精确重构。

1　CS和BSBL的概述

1.1 CS CS理论认为，只要信号是可压缩的或在某个变换域上可进行稀疏变化的，那么就可以用一个与变换基不相关的测量矩阵稀疏变换后的高维信号投影到一个低维空间上，然后通过求解优化问题就可以从这些少量的低维投影中精确地重构出原始信号。CS框架下的信号压缩采样过程见图1。

图1 CS理论框架

假设一个x∈RN离散信号向量在某正交基Ψ下是K稀疏的，则信号 x可以表示为：

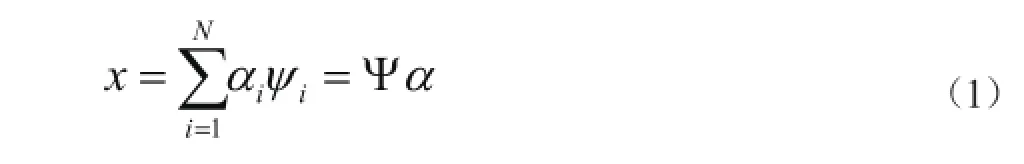
其中，αi在正交基Ψ展开的N×1维的系数向量，且只有K（K＜＜N）个元素非零，Ψi为正交基Ψ的行向量。

多数自然信号都具有丰富的结构，其中块结构（block）是一种广泛存在于自然信号的结构。如果待测信号具有块结构，就可以被看作为一系列块的连接，如：

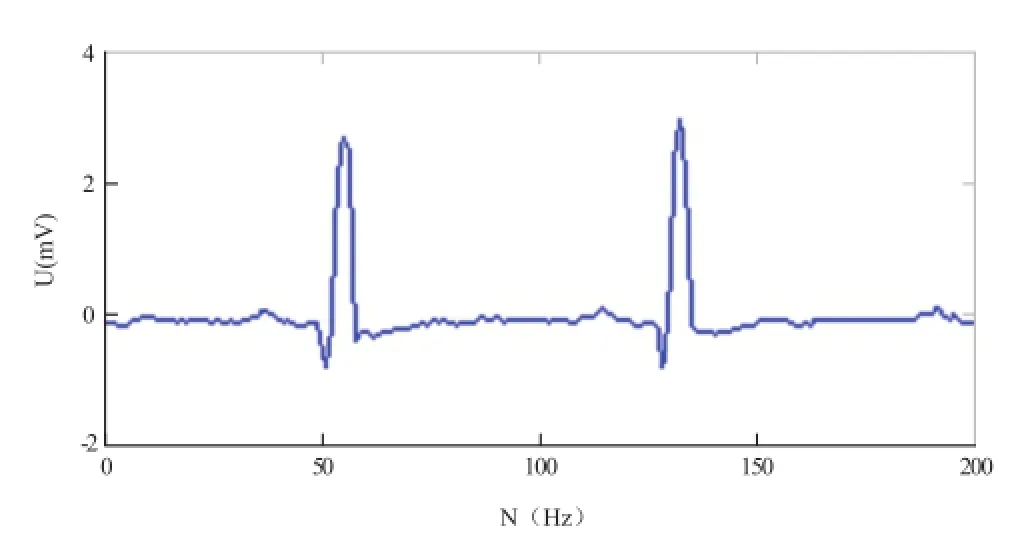
图2 一段含有200个点的心电数据

1.2 BSBL 在块稀疏CS模型中，假设每γi个块xi都满足多元高斯分布，且其中每块相互独立：

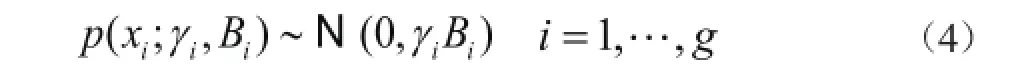
其中，γi是一个非负参数，决定块xi的稀疏性。当γi=0时，对应的第i块（xi）值为零。Bi∈Rdi×di是正定矩阵，用于描述块内元素之间的相关结构。假设块之间相互不相关，公式（4）可记为p（x）～N（0, Σ0），式中Σ0是一个由γiBi给出第i个块的块对角矩阵。假设噪声向量满足多元高斯分布，即p（v）～N（0, λI），式中λ是一个正标量。则x的后验概率分布为：其中，当参数被估计出来，x的最大后验（MAP）估计就能够直接得到。利用第二类最大释然估计可以估计出BSBL框架中的参数：

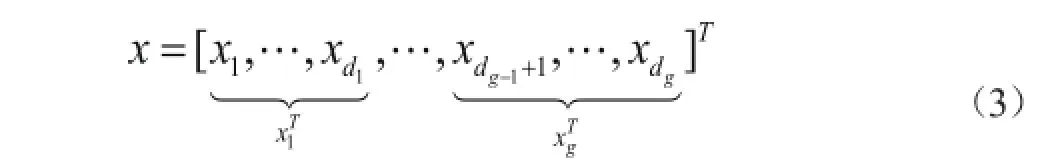
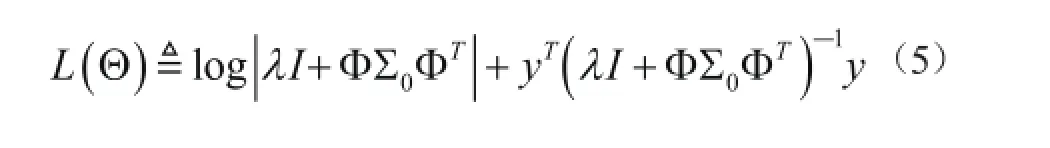
式中，xi=Rdi×1，且di（i=1,..., g）块长度不一定都是相同的，而非零元素集中在少数几个块内，利用这样的块结构能够有效地提高重构效果。

MIT-BIH心律数据库中获取的心电数据大致可以视为一个含噪的非稀疏信号。图2为一段心电数据记录，在这段时间轴上，45～60和120～135之间可以看作是非零块，其他的可以看作是零块的连接，整个就是一个受到噪声污染的心电信号。实际的心电记录即是在未知块分区、未知信号噪声情况下建模的块稀疏信号。

然而，利用未知块分区来重建原始信号是非常困难的。因此，目前在这方面的CS算法非常少。而本文应用BSBL框架及其派生算法，相比于Group Lasso、Block-OMP等恢复块稀疏信号的方法，BSBL考虑了块内元素间的相关性，得到的重构效果更加理想［6］。对式中利用EM（Expectation Maximization）方法求解得下面的迭代算法：

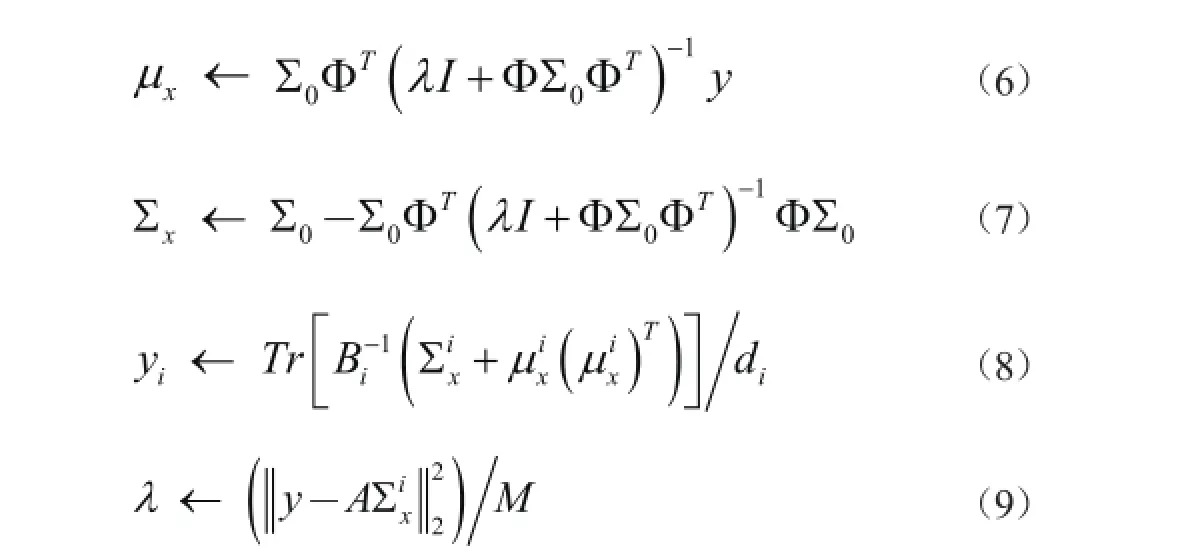
同样，可以利用EM方法得到每个Bi的学习规则。然而，用不同的Bi设定每个块会导致过分拟合。为避免过拟合，文献［ 6］采用一阶AR模型表示块内相关，并设计了正定对称阵近似。具有以下形式：

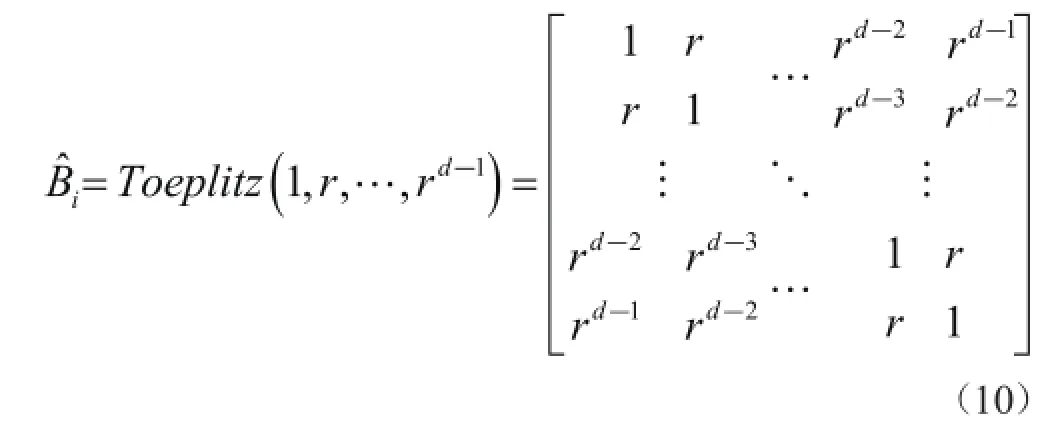
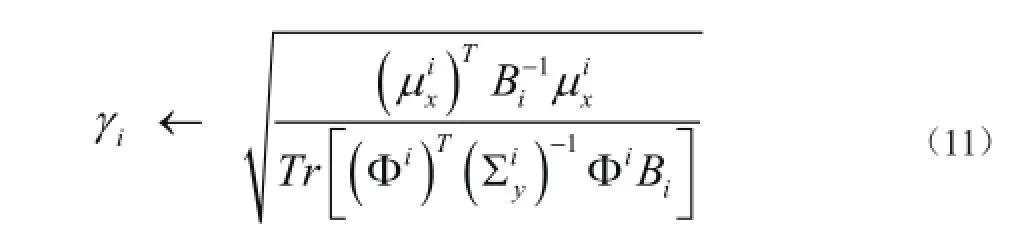
BSBL重构算法首先揭示了块内相关对块稀疏信号重构性能的影响，并且是对非稀疏信号进行重构的算法。Zhang等［5］的研究已证明在无噪声情况下BSBL给出的稀疏解即为全局解。

2　实验及结果分析

本文选择MIT-BIH心律数据库中心电数据进行实验。对比了在傅里叶稀疏基、离散余弦稀疏基、小波稀疏基［8］下心电信号的稀疏度；并测试了信号在BSBL算法下的重建效果。实验相关参数设置：心电信号选取arrhythmia信号，截取信号前1024个点作为测试信号，并按16个点长均匀分块；观测矩阵选用每列包含15个非0元素，大小为512×1024的稀疏随机矩阵。重构信号质量选用RMSE来评价，RMSE ＜9%的重构信号可用于医学诊断［6］，且RMSE越小，表明失真越小，误诊概率越低。

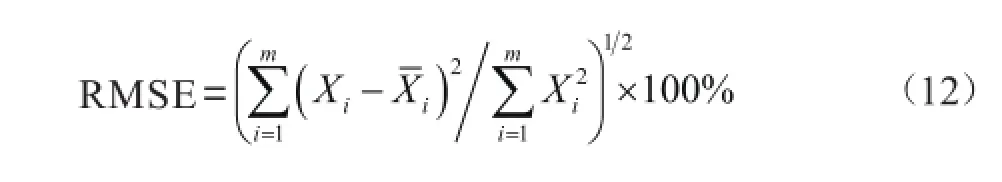
图3为MIT-BIH数据库中arrhythmia信号前1024个点在各稀疏基下稀疏度表示。从图中可以清楚地看出信号在稀疏基下并非稀疏（或不够稀疏）。而CS的前提条件是信号足够稀疏。若要人为地构建一个只适用于某个信号的稀疏基，根本无意义且浪费时间。而BSBL算法能很好地克服信号非稀疏所带来的不便，高质量的重构出原始信号。

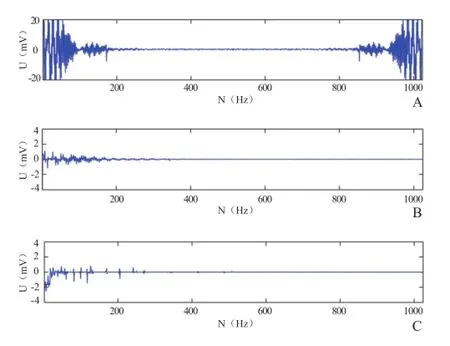
图3 arrhythmia信号的稀疏性表示。A、B、C分别为傅里叶稀疏基、离散余弦稀疏基、小波稀疏基下心律失常信号

图4、5是normal sinus rhythm、arrhythmia信号的前1024个点在BSBL算法下的重构效果。图4是在不利用块内相关性的重构效果图，从图中对比效果可以看出其效果极差，根本不能用于临床诊断，而图5利用了块内相关性，重构质量明显提高。

改变观测矩阵维度M，采用1024点的arrhythmia信号在正交匹配追踪（OMP）算法和BSBL算法下进行重构，测量观测矩阵维度变化对应RMSE的关系（图6）。信号的RMSE都随着测量维度的增加而降低在图中可以看到， OMP算法重构的心电信号质量并不理想，无法达到临床要求。而BSBL算法下恢复信号的RMSE均保持在9%以下，表明BSBL能够高精度地重构非稀疏的心电信号，且压缩比CR=M/N=1/8，能够有效地减少采样频率，降低功耗。

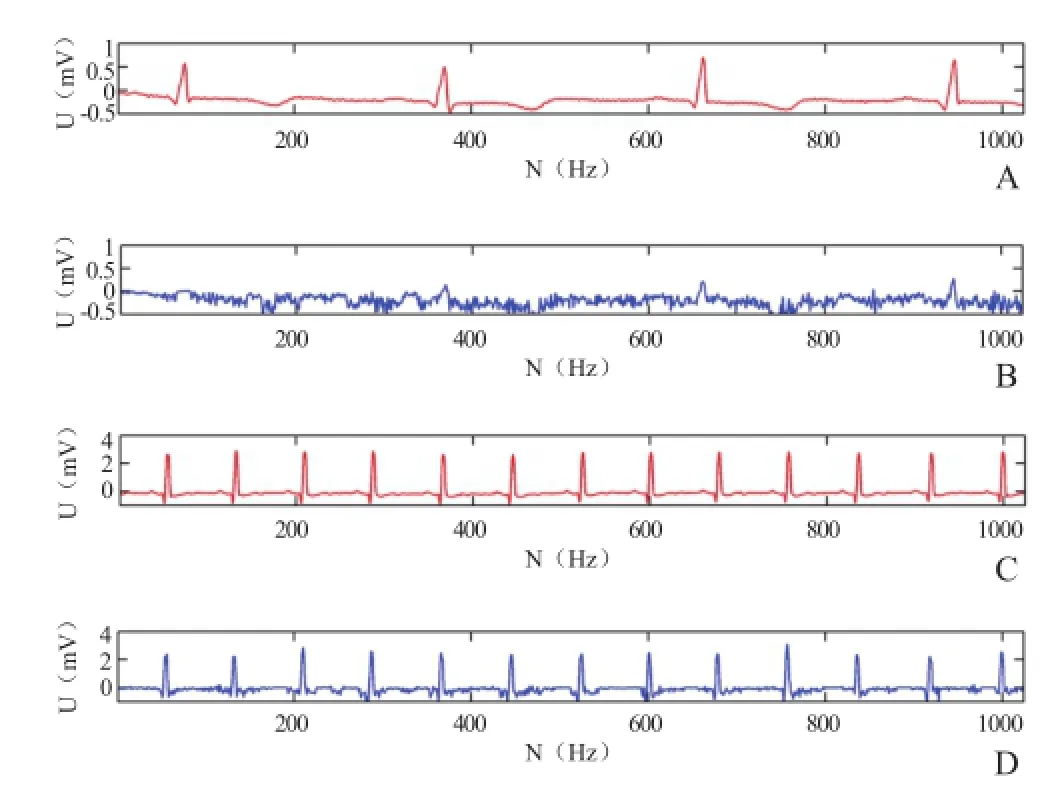
图4 不利用块内相关性的重构效果。A为原始心电信号（心律失常）；B为心律失常BSBL算法不利于块内相关性的重构效果；C为原始心电信号（正常窦性心律）；D为正常窦性心律BSBL算法不利于块内相关性的重构效果

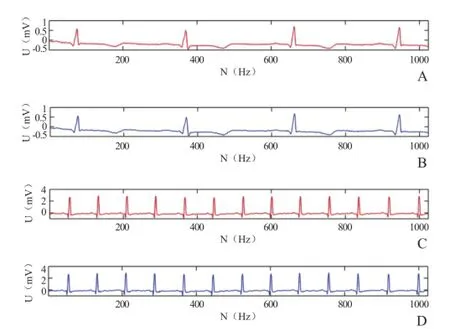
图5 利用块内相关性的重构效果。A为原始心电信号（心律失常）；B为心律失常BSBL算法利于块内相关性的重构效果；C为原始心电信号（正常窦性心律）；D为正常窦性心律BSBL算法利于块内相关性的重构效果

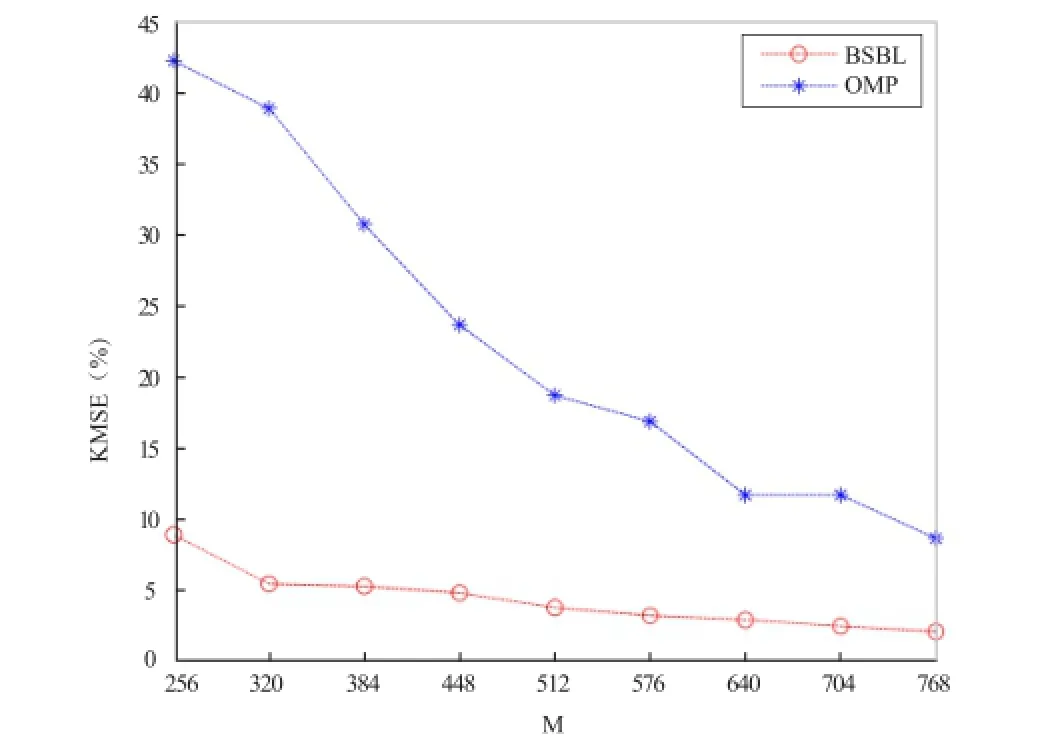
图6 两种算法下的测量维度M与重构RMSE

3　结论

针对非稀疏心电信号精确的CS重构，本文采用BSBL算法框架重构心电信号。算法利用块结构以及块内相关性描述心电信号，并采用最大似然估计方法对参数进行估计。实验结果表明BSBL算法能够高质量重构非稀疏心电信号，降低对数据的采样频率，从而降低功耗并减少了采集数据，缓解存储压力。尽管运用BSBL算法能高精度重构心电信号，但要在医学信号领域方面运用仍不够完善，存在一定的改进空间。

参考文献

［1］ Candes EJ, Romberg J, Tao T. Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 2006, 52（2）： 489-509.

［2］ Mamaghanian H, Khaled N, Atienza D, et al. Compressed sensing for real-time energy-efficient ECG compression on wireless body sensor nodes. IEEE Trans Biomed Eng, 2011, 58（9）： 2456-2466.

［3］ Dixon AM, Allstot EG, Gangopadhyay DA. Compressed sensing system considerations for ECG and EMG wireless biosensors. IEEE Trans Biomed Circuits Syst, 2012, 6（2）： 156-166.

［4］ Zhang Z, Jung TP, Makeig S, et al. Compressed sensing of EEG for wireless telemonitoring with low energy consumption and inexpensive hardware. IEEE Trans Biomed Eng, 2013, 60（1）： 221-224.

［5］ Zhang ZL, Rao BD. Sparse signal recovery with temporally correlated source vectors using sparse bayesian learning. IEEE J Sel Top Signal Process, 2011, 5（5）： 912-926.

［6］ Zhang Z, Rao BD. Recovery of block sparse signals using the framework of block sparse bayesian learning. IEEE International Conference, 2012： 3345-3348.

［7］ 罗堪, 李建清, 王志刚, 等. 心电压缩感知恢复先验块稀疏贝叶斯学习算法. 仪器仪表学报, 2014, 35 （8）： 1883-1889.

［8］ 尹宏鹏, 刘兆栋, 柴毅, 等. 压缩感知综述. 控制与决策, 2013, 28（10）： 1441-1445, 1453.

（本文编辑冯 婕）

作者单位中国计量学院信息工程学院 浙江杭州310018

Doi：10.3969/j.issn.1005-5185.2016.03.020

通讯作者陈少峰

中图分类号

TN911.7

收稿日期：2015-08-12

Electrocardiograph Reconstruction Based on Block Sparse Bayesian Learning Algorithm

【Abstract】Compressed sensing （CS） has the advantages of low cost and low powe consumption in the application of ECG signal, but the quality of the existing algorithm to reconstruct the non-sparse ECG signal is not ideal. This paper introduces an ECG data reconstruction method based on the theory of the compressed sensing. Block spar bayesian learning （BSBL） algorithm combined with intra-block correlation is used to efficiently reconstruct ECG data from MIT-BIH database. The simulation results show tha the method can accurately reconstruct ECG signal, compared to traditional CS algorithm with lower root mean square error （RMSE）, and reconstruction quality is improved significantly. BSBL algorithm can efficiently reconstruct the non-sparse ECG signal reducing the use of sensors and power consumption.

【Key words】Signal processing, computer-assisted； Compressed sensing； Algorithms Block sparse bayesian learning