Matlab在高中数学学习中的应用

欧阳仁泽

【摘 要】本文将Matlab应用于高中数学学习，并以一元二次函数和幂函数为例进行了仿真绘图，从图中可清晰得出各函数的特征。从而表明，将Matlab应用于高中数学的可视化学习，有利于更好的掌握和理解函数知识，提高自身的动手能力和学习兴趣，并在此过程加深对所学内容的理解。

【关键词】Matlab；高中数学；函数

Matlab是Mathworks公司推出的集科学计算、图像可视化、声音处理于一体的高级语言[1]。其良好的性能，使得功能简单，易学易用，让繁琐的程序简单化，程序开发时间短，是数学学习的一个有效工具。《普通高中数学课程标准》鼓励学生借助信息技术学习有关数学内容。因此，本文就matlab工具在数学学习上的应用，通过绘制一元二次函数和幂函数图形，供大家参考。

1 Matlab在高中数学中的常用命令

2 一元二次函数

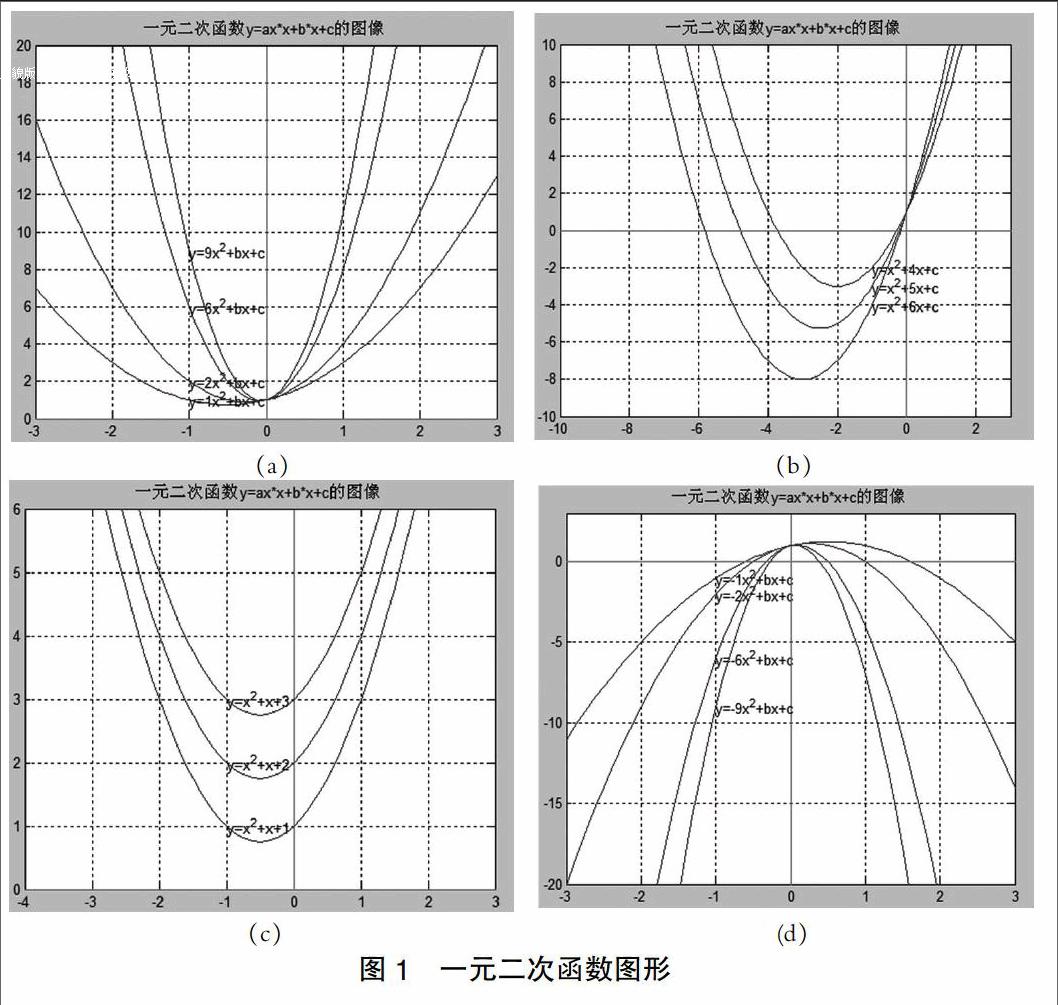
一元二次函数y=ax2+bx+c，（a≠0）的学习中要求掌握：（1）一元二次函数图像的画法及图像的特征，比如开口方向、开口大小、对称轴位置等等；（2）一元二次函数的性质，能利用性质解决实际问题；（3）二次函数在指定区间上的最大（小）值；（4）一元二次函数、一元二次方程的关系。这些性质的掌握可以从两方面入手：一是解析式，二是图像特征。从解析式出发，可以进行纯粹的代数推理求解问题；从图像特征出发，可以实现数与形的自然结合，这正是中学数学学习中一种非常重要的思想方法。在Matlab中可以改变参数，画出图形从而获得图像特征，部分程序如下：

for a=[1 2 6 9]；

b=1；

c=1；

x=-30：0.1：30；

y=a*x.*x+b*x+c；

y1=0*x；

plot（x，y1，'m'，y1，x，'m'，x，y）；

title（['一元二次函数y=ax*x+b*x+c的图像']）；

text（-1，a*（-1）^2+b*（-1）+c，['y='，num2str（a），'x^2+bx+c']）；

grid on

axis （[-3 3 0 20]）；

pause（1）

hold on

end

图1中当参数a，b，c变化时，二次函数图形发生改变，可以得到一元二次函数中各系数对图形的影响。由图1（a）、（d）可知，a值发生改变时，抛物线的开口大小和开口方向发生改变，同时对称轴和顶点坐标也发生改变。当a>0时，抛物线开口朝上，a越大，开口越小，抛物线越陡，顶点越高，对称轴越靠右；当a<0时，抛物线开口朝下，a越大，开口越大，抛物线越陡，顶点越高，对称轴越靠右。由图1（b）可知系数b发生变化时，抛物线的开口大小、开口朝向、与轴的交点坐标都不变，对称轴和顶点坐标均有变化；系数c发生变化时，抛物线形状不变，只是上下平移。

3 幂函数

编写Matlab程序，运行结果如图2所示。部分程序如下：

for a=[-1/2 -1/3]；

x=-100：0.05：100；

y=x.^a；

y1=0*x；

plot（x，y1，'m'，y1，x，'m'，x，y）；

% plot（x，y）；

title（['幂函数x^a的图像']）；

if a<1；

text（5，（5）^a，['y=x^'，num2str（a）]）；

else

text（2，2^a，['y=x^'，num2str（a）]）；

end

grid on

axis （[-10 10 -2 2]）；

pause（1）

hold on

end

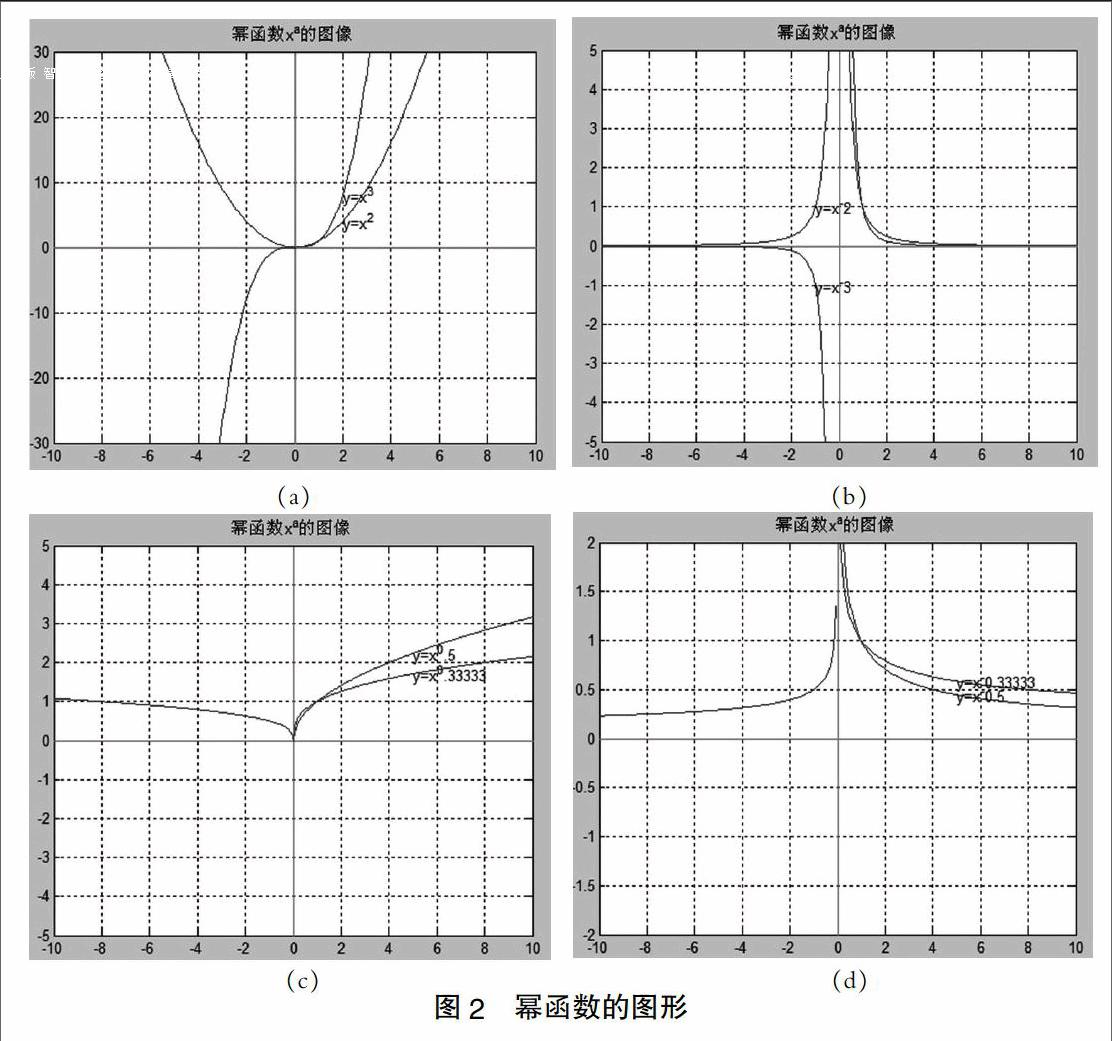
从图2中，幂函数y=ax（a∈R）的图像我们分几种情况讨论：

（1）指数a≥1时，如图a所示。a为偶数，则函数为偶函数，其图形关于y轴对称，在x轴左侧为单调递减，在x轴右侧为单调递增。a为奇数，则函数为奇函数，在整个定义域上为增函数。

（2）指数a≤-1时，如图b所示。a为偶数，则函数为偶函数，其图形关于y轴对称，在x轴左侧为单调递增，在x轴右侧为减函数。如果a为奇数，则函数为奇函数，图像在第一、三象限各象限内单调递减。

（3）指数0

（4）指数-1

（5）幂函数的图形不过第四象限。

4 结束语

本文列举一元二次函数和幂函数在Matlab上的仿真绘图，从绘图中可清晰分析出各自的特征，说明将Matlab应用于高中数学的可视化学习，有利于更好的掌握和理解函数知识，提高自身的动手能力和学习兴趣，并在此过程加深对所学内容的理解。利用Matlab对数学点进行仿真，激发了自身对数学知识的求知欲和主动探索的精神，从而获得良好的学习效果。

【参考文献】

[1]于坚.利用Matlab软件辅助高中数学教学[J].中小学信息技术教育，2006，55：7-77.

[2]刘浩，韩晶.MATLAB R2014a完全自学一本通[M].北京：电子工业出版社，2015，1.

[3]王晖.Matlab在高中数学“函数”教学中的应用.数学教学研究[J].2015，3：11-14.

[责任编辑：杨玉洁]