奇异值分解用于可调谐二极管激光吸收光谱技术去除系统噪声
王 喆,汪 曣,张 锐,赵学玒*,刘乔俊,李丛蓉
1. 天津大学精密仪器与光电子工程学院,天津 300072
2. 天津科技大学电子信息与自动化学院,天津 300222
奇异值分解用于可调谐二极管激光吸收光谱技术去除系统噪声
王 喆1,汪 曣1,张 锐2,赵学玒1*,刘乔俊2,李丛蓉2
1. 天津大学精密仪器与光电子工程学院,天津 300072
2. 天津科技大学电子信息与自动化学院,天津 300222
可调谐二极管激光吸收光谱(TDLAS)技术用于气体浓度检测时,会受到谐波检测中基线漂移及噪声的影响,因此如何去除系统噪声一直是研究的热点。分析了连续截断信号和构造hankel矩阵两种不同方法下,奇异值分解(SVD)对TDLAS系统检测的理论意义。将二次谐波信号分别用该方法进行矩阵化排列和奇异值分解,选取适当阈值将部分奇异值置零并重构矩阵,得到了这两种方法对基线纠漂和去噪的不同效果。实验证明,奇异值分解方法不需加入额外系统部件、不需通零气扣除背景,就能够快速有效地去除TDLAS系统噪声,而构造hankel矩阵的方法适用于去除高频噪声,连续截断信号的方法适用于进行基线纠漂。将该方法应用于实际TDLAS系统氨气检测时的二次谐波,系统噪声去除率达80%。
奇异值分解;可调谐二极管激光吸收光谱;基线纠漂;去噪
引 言
可调谐二极管激光吸收光谱(tunable diode laser absorption spectroscopy)技术常用于气体浓度测量,具有分辨率高、选择性强、探测灵敏度高、响应速度快等优点[1-2]。但在实际测量中,由于待测气体浓度常为毫克每立方米至纳克每立方米量级,容易受到系统噪声的影响。在实际TDLAS系统中,噪声主要来自四个方面:探测器噪声、激光额外噪声、剩余幅度调制(RAM)引起偏移噪声和光学干涉条纹[3]。目前去除系统噪声的方法包括:提高检测频率、缩小带宽;使用高稳定性恒流源、使用液态制冷剂控温[3-4];通入零气扣除背景[5];精细光路[1]等。但这些方法都一定程度上,受到硬件本身性能的限制,不能满足测量需求,且需要加入新的元件或增加检测步骤,故需要加入数字滤波方法。常用的数字滤波方法有:算数平均、滑动平均、非线性最小二乘、小波变换、最大相关等[5-6],但它们不同程度上存在着方法简单,对有用信号影响大、不能同时满足去除各种系统噪声的要求、计算耗时长、实际应用时需更换选择合适线型、信号与噪声频率混叠时难以分辨等问题。奇异值分解(singular value decomposition)是矩阵论中常用的矩阵分析方法,具有降噪、提取信号特征等功能[7-9]。目前在激光和光谱中的应用主要包括:去除激光器噪声、长时检测中监测温度变化或机械振动、提取背景信号等[10-13]。但没有对奇异值分解方法应用于TDLAS系统对气体浓度进行测量时,不同的构造矩阵方法是否对去除各种系统噪声存在差异做研究。本文将奇异值分解方法用于TDLAS系统去除高频噪声和进行基线矫正,分析对于系统中不同类型噪声的去除所适用的不同构造矩阵进行奇异值分解的方法。
1 原理介绍
1.1 TDLAS原理
TDLAS属于红外吸收光谱检测的一种,它基于朗伯-比尔定律(Lambert-beer Law),采用波长调制技术加入正弦电流进行调制。当激光的中心频率受到频率为的正弦波信号调制时,其瞬时频率为
(1)
其中να为调制幅度,ωα调制频率。则透过光强可以用余弦傅里叶级数来表示
(2)
当n>0时,各次谐波分量可以表示为
(3)
其中θ=ωmt。通常采用二次谐波信号进行测量,只要得到二次谐波信号和原始光强,就可以反演出气体浓度。
1.2 奇异值分解原理
奇异值分解是线性代数中一种矩阵分解方法,若X是一个n×m维矩阵(X∈Rn×m),对其进行奇异值分解可以得到
(4)
其中,U和V分别是n×n维和m×m维酉矩阵,Σ为n×m维非负对角阵,其对角元素就是矩阵X的q个奇异值λi,且λi按从大到小递减顺序排列,VT为V的共轭转置。
奇异值分解可以实现将矩阵分解到n维和m维的两个空间正交基上,并对奇异值进行降序排列,且可以根据UΣVT重构原始矩阵。
1.3 奇异值分解二次谐波信号
将原始二次谐波信号构造成矩阵时,有不同的方式,不同的方式分解后的效果不同。本文采用连续截断信号和构造hankel矩阵两种方式对原始二次谐波进行处理。
1.3.1 构造连续截断信号矩阵
将一组离散的二次谐波信号I={i1(1),i1(2),i1(3),…,in(m)}构造成一个n×m维hankel矩阵I(I∈Rn×m)
(5)
矩阵中每一行是一个完整的二次谐波信号,横向代表扫描频率的变化,纵向代表时间的变化。对矩阵I进行奇异值分解可以得到
(6)
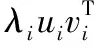
(7)
通过构造连续截断信号矩阵的方法,将二次谐波信号分解到频率和时间两个不同的子空间中,不同的奇异值大小代表不同频率和时间下信号分量xi的投影大小,xi叠加可以重新构成原始二次谐波信号。
1.3.2 构造hankel矩阵
将一组离散的二次谐波信号I={i(1),i(2),i(3),…,i(N)}构造成一个n×m维hankel矩阵I(I∈Rn×m)
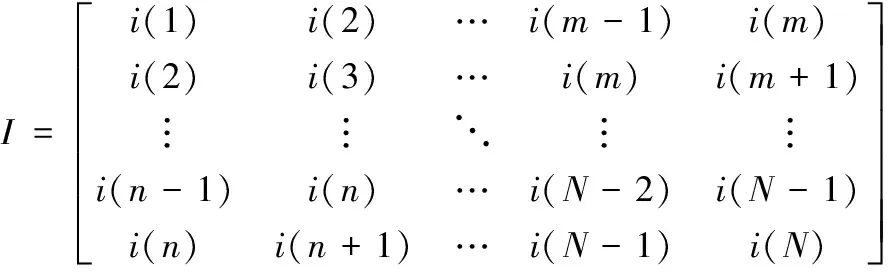
(8)
其中矩阵I的第一行前m-1个元素与第m列首尾相接即为原始二次谐波信号,对矩阵I进行奇异值分解可以得到
(9)
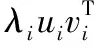
(10)
每一个λiuivTi矩阵的第一行前m-1个元素和第m列首尾相接都构成原始二次谐波信号的一个分量xi,xi叠加可以重新构成原始二次谐波信号。
对二次谐波信号进行奇异值分解的本质是将原有信号分解到两个不同的向量空间中进行投影,xi反映原始二次谐波信号在两个不同向量空间标准正交基vi和ui上的投影大小,对应分量越大,代表检测到的二次谐波信号与这两个标准正交基的相似程度越大。λi为原始二次谐波信号的i个不同的奇异值,且按大小降序排列。可以认为,原始二次谐波信号矩阵I是由真实二次谐波信号和噪声共同组成的矩阵,分别包含了气体吸收信号和噪声信号
(11)
而λi的大小可以反映信号和噪声能量集中的情况,前p个较大的奇异值主要反映气体吸收信号,后(i-p)个较小的奇异值则主要反映噪声信号,若把这部分反映噪声的奇异值置零,则就将其对应的分量xi-p从原始二次谐波信号中扣除,利用新的奇异值非负对角阵重构矩阵,就可以还原出真实的气体吸收信号
(12)
1.4 TDLAS系统噪声来源
在实际TDLAS系统中,噪声来自四个方面:探测器噪声、激光额外噪声、剩余幅度调制(RAM)引起偏移噪声和光学干涉条纹。
探测器噪声主要包括:散粒噪声、热噪声和1/f噪声。其中散粒噪声的引起因素是:当激光进入探测器被接收时,由于不均匀发射,会产生一部分光子噪声。这部分噪声与调制频率无关,是由光功率强度引起。而系统中热噪声引起原因是:器件材料中电子的无规则热运动引起的波动噪声。其大小由温度和检测时的激光带宽影响。1/f噪声则由探测器结构决定,由半导体之间的连接决定,在检测频率<1 kHz时,它是属于光电转换元件的探测器噪声中的主要部分。但频率>1 kHz时,主要部分变为散粒噪声和热噪声。对于探测器噪声来说普遍具有白噪声的频谱特性,且多数由制造工艺或器件本身来决定,因此目前主要通过提高检测频率的方法来抑制这部分噪声。
激光额外噪声指激光器输出功率波动,进而影响到DFB激光器的注入电流值,从而影响系统的检测灵敏度。其噪声来源多种多样,包括:激光器自身噪声、振动、电流或温度调制时输入信号的不稳定性。所以应对的方法主要为增加系统部件,对其稳定性加以控制,减小振动、电流、温度等的变化,或减小信号的检测带宽等。
波长调制技术在对波长进行调制而提高系统检测灵敏度的同时,也对激光光强进行了强度强制,其中线性部分为幅度调制,而非线性部分就引起与气体吸收无关的RAM,它的大小由光强调制和频率调制间的非线性相位移动和非线性程度的系数来决定。RAM的存在会引起二次谐波信号的畸变,造成基线漂移。目前多采用通入零气进行扣背景的方法来减小RAM,但这样做加入了检测步骤和计算量,十分繁琐。
在TDLAS系统中,不可避免地存在光路系统,而光路中所有光学元件的标准具效应(F-P谐振腔干涉)、反射和散射就引起了正弦信号(波长范围10-3~10-2cm-1)形式的光学干涉条纹叠加,且易受到温度、机械震动等的影响。由于它的存在使透射光信号将发生变化,从而不只携带有气体的吸收信息。光学干涉条纹对系统检测的影响随光程长变化而变化,而其变化情况也不唯一,包括了频率和包络的变化。其中,对于频率部分,随光程增大而增大;而对于包络部分,随光程增大而减小。因此对长光程气体池来说光学干涉条纹的影响更小,而短池中多次反射引起的系统噪声,则很难被消除。
而在TDLAS系统中,通过对氨气浓度检测中二次谐波的探测发现,系统噪声的形式包括高频噪声和基线漂移。其中高频噪声主要来自于探测器和激光额外噪声,基线漂移主要由RAM和光学干涉条纹引起。
2 仿真实验与结果
仿真模拟系统运用Matlab软件中的Simulink环境下丰富的模块库,基于实际的TDLAS系统结构,根据系统传递函数的数学关系模型,建立了光源模块、吸收气室模块和数据检测处理模块,依据洛伦兹吸收线型函数模拟出气室吸收过程和二次谐波信号曲线。系统总结构图如图1。
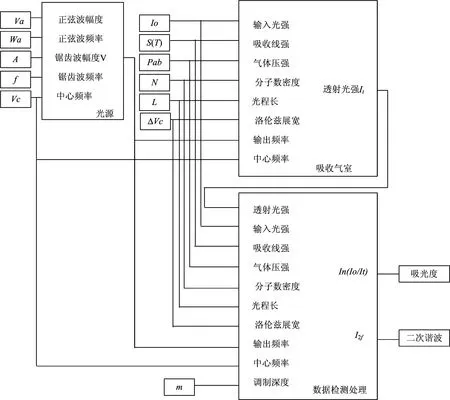
图1 TDLAS仿真模拟系统整体结构
2.1 标准二次谐波
实验中采用10 Hz锯齿波信号和30 kHz正弦波信号,待测气体吸收谱线中心值为6 731 cm-1(1 486 nm),输入光强I0=300 a.u.,气体压强Pabs=1 atm,气体分子数密度N=0.5%,光程长L=14.9 cm,气体吸收线强S(T)=0.036(cm-2·atm-1),调制深度m=2.2。模拟系统得到的标准二次谐波信号如图2。
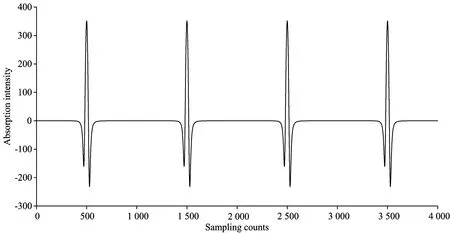
图2 标准二次谐波曲线
由图2可以看到,二次谐波信号I2f存在峰值,此时的气体吸收幅度最大。图中模拟得到的二次谐波,主要包括前三阶傅里叶分量。曲线形状主要由二阶傅里叶分量决定,而一、三阶的奇次分量使二次谐波曲线相对于呈偶对称的二阶傅里叶分量在线型对称性上发生了改变。但奇次谐波分量在吸收线型中心位置为零,对二次谐波的改变只发生在波形两翼,对于波形中心峰值并没有改变,因此可以通过对二次谐波信号峰值的测定实现浓度的反演。
2.2 奇异值分解方法去除高频噪声
将模拟出的含有高频噪声的原始二次谐波信号[图3(a)、图4(a)]分别按照连续截断信号的方式(图3)和形成hankel矩阵的方式(图4)构造原始矩阵,分别对它们进行奇异值分解,得到了不同方式构造矩阵时的奇异值曲线,如图3(c)和图4(c)。而对于奇异值的置零只要包括三种方法:将低于奇异值曲线拐点的奇异值置零、将低于奇异值均值的奇异值置零、将低于奇异值中值的奇异值置零。图中低于奇异值曲线拐点处的那些奇异值相对较小,选择将它们置零后,得到新的奇异值曲线,如图3(d)和图4(d),运用新的奇异值矩阵重构二次谐波矩阵,就可以得到处理后的二次谐波信号。
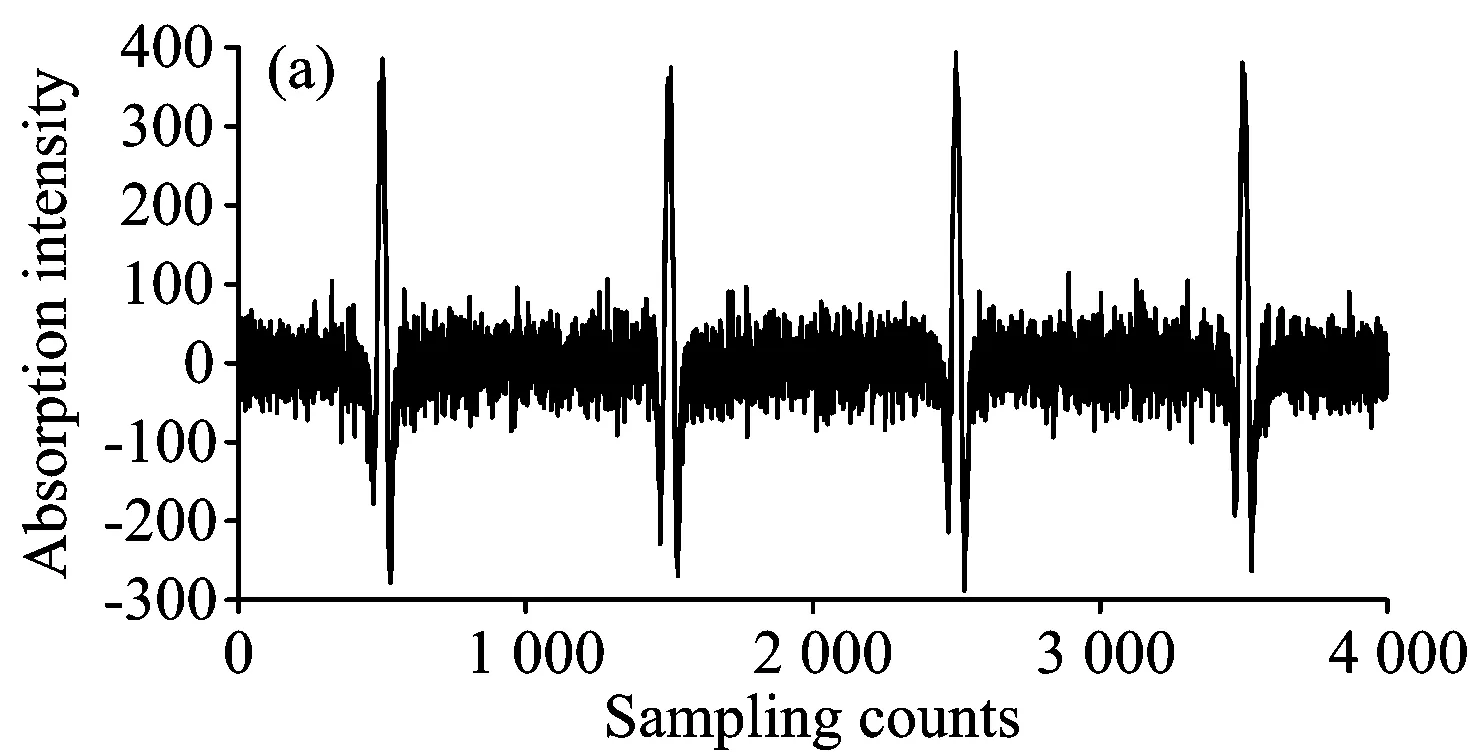
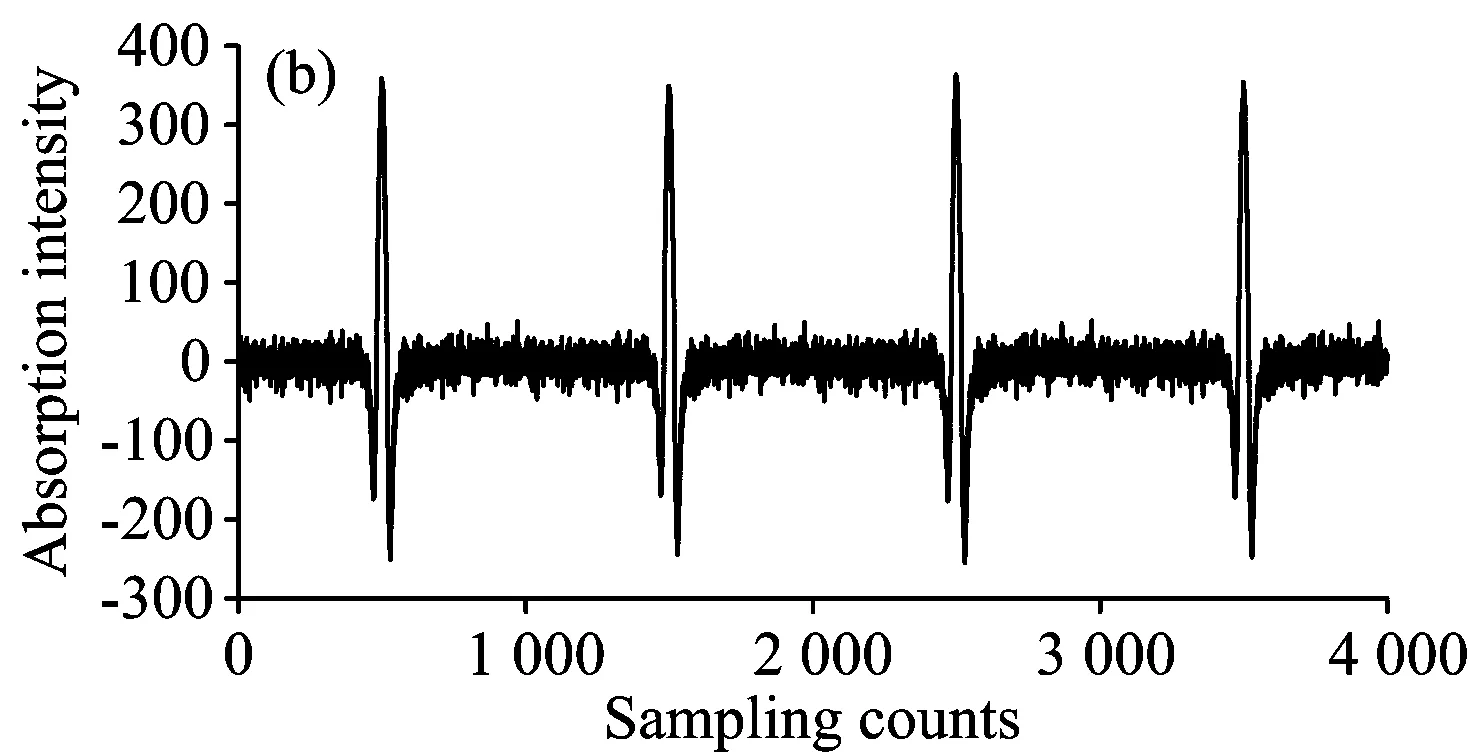
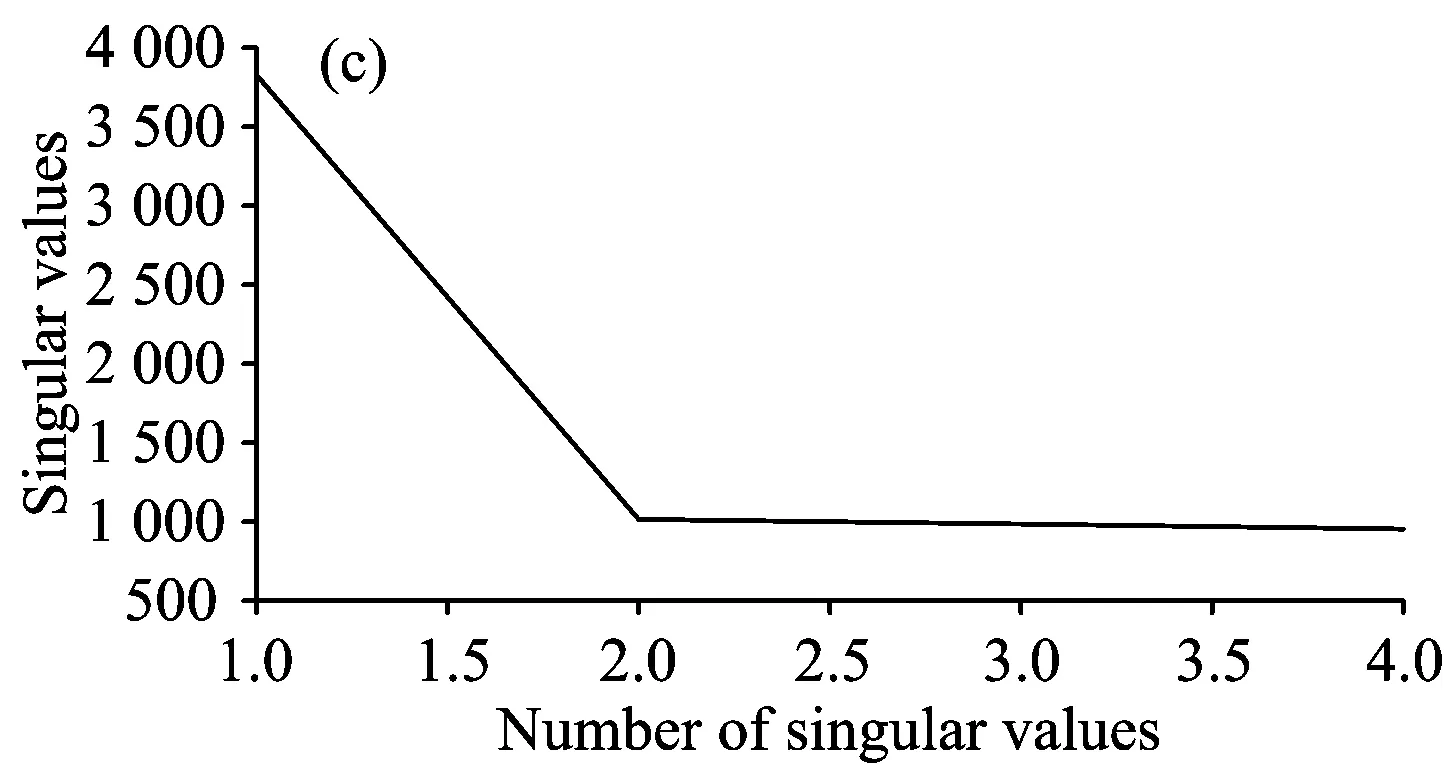

图3 构造连续截断信号矩阵方法去除高频噪声
从图3(b)和图4(b)中明显可以看出两种方法均具有去噪功能,但去噪能力有所不同。使用连续截断信号的方法去噪后的二次谐波与原始曲线相比,相对标准曲线的均方误差提高了15.5,噪声去除率为50%。而hankel矩阵的方法比连续截断信号方法处理效果要好,信号均方误差提高了23.0,噪声去除率达到73%。
进一步分析两种不同方法去除高频噪声时效果的不同,TDLAS系统中的高频噪声主要来源于探测器噪声,包括散粒噪声、热噪声和1/f噪声,具有白噪声的信号特点[3]。这些高频噪声叠加在相对低频的二次谐波信号上时,二次谐波的检测则要受其影响,而使用构造hankel矩阵的方法将信号分解到两个不同子空间,可以有效地从原始信号中,提取出特征不同的二次谐波信号和高频噪声。而高频噪声存在于检测的整个过程,使用连续截断信号的方法,在时间子空间中二次谐波信号与高频噪声信号没有明显差异,故对于高频噪声进行去除的效果不如构造hankel矩阵的方法。
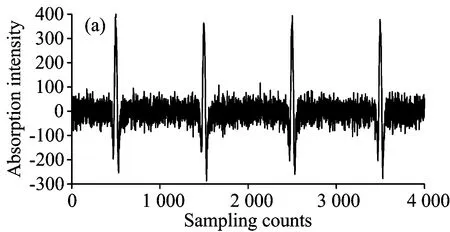
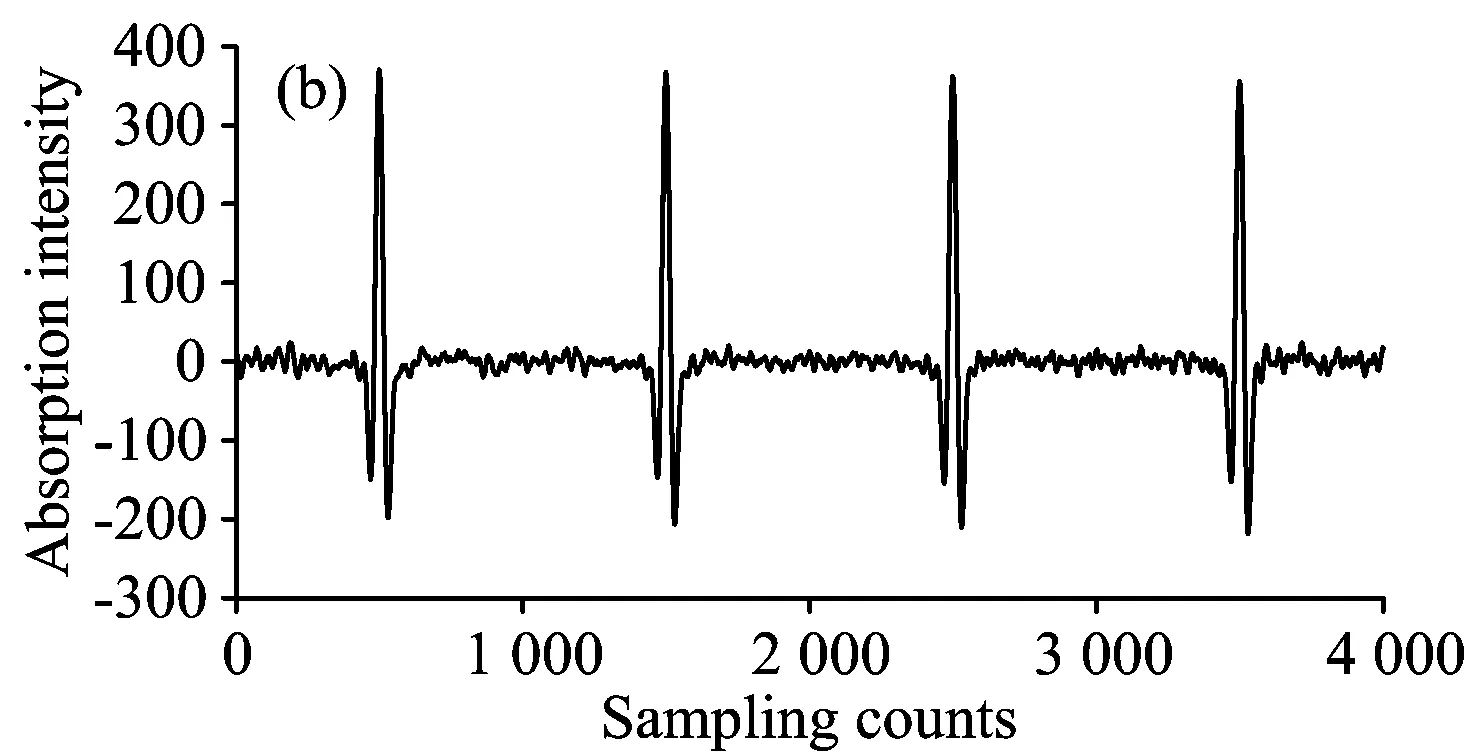


图4 构造hankel矩阵方法去除高频噪声
2.3 奇异值分解方法进行基线纠漂
将模拟出的基线产生漂移的原始二次谐波信号[图5(a)、图6(a)]分别按照连续截断信号的方式(图5)和形成hankel矩阵的方式(图6)构造原始矩阵,使用同样的方法分别对它们进行奇异值分解、奇异值置零和矩阵重构,得到去除基线后的二次谐波信号。
从图5(b)和图6(b)中明显可以看出使用连续截断信号的方法能够去除基线漂移,但构造hankel矩阵时对基线漂移没有去除效果。使用连续截断信号的方法去噪后的二次谐波与原始曲线相比,相对标准曲线的均方误差提高了27.2,基线去除率达到78%。


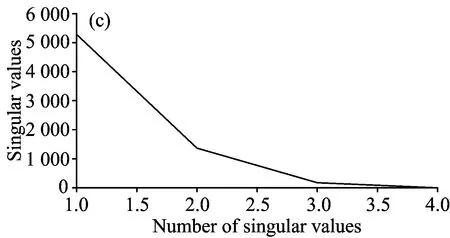

图5 构造连续截断信号矩阵方法基线纠漂
进一步分析两种不同方法去除基线效果的不同,TDLAS系统中的基线漂移主要由剩余幅度调制(RAM)和光学干涉条纹引起。光强调制中的非线性部分引起与气体吸收无关的RAM;光路中光学元件的标准具效应、反射和散射引起了正弦形式的光学干涉条纹,且易受到温度、机械震动的影响。因此基线漂移相比二次谐波信号是一种低频噪声,且为一种时变的噪声信号。所以使用hankel矩阵的方法将信号分解到两个不同子空间,无法有效的提取信号特征。而连续截断信号的方法,在时间子空间中,其他条件不变时,二次谐波信号不随时间而变化,但基线存在漂移,故进行基线矫正时采用连续载断信号的方法更为有效。
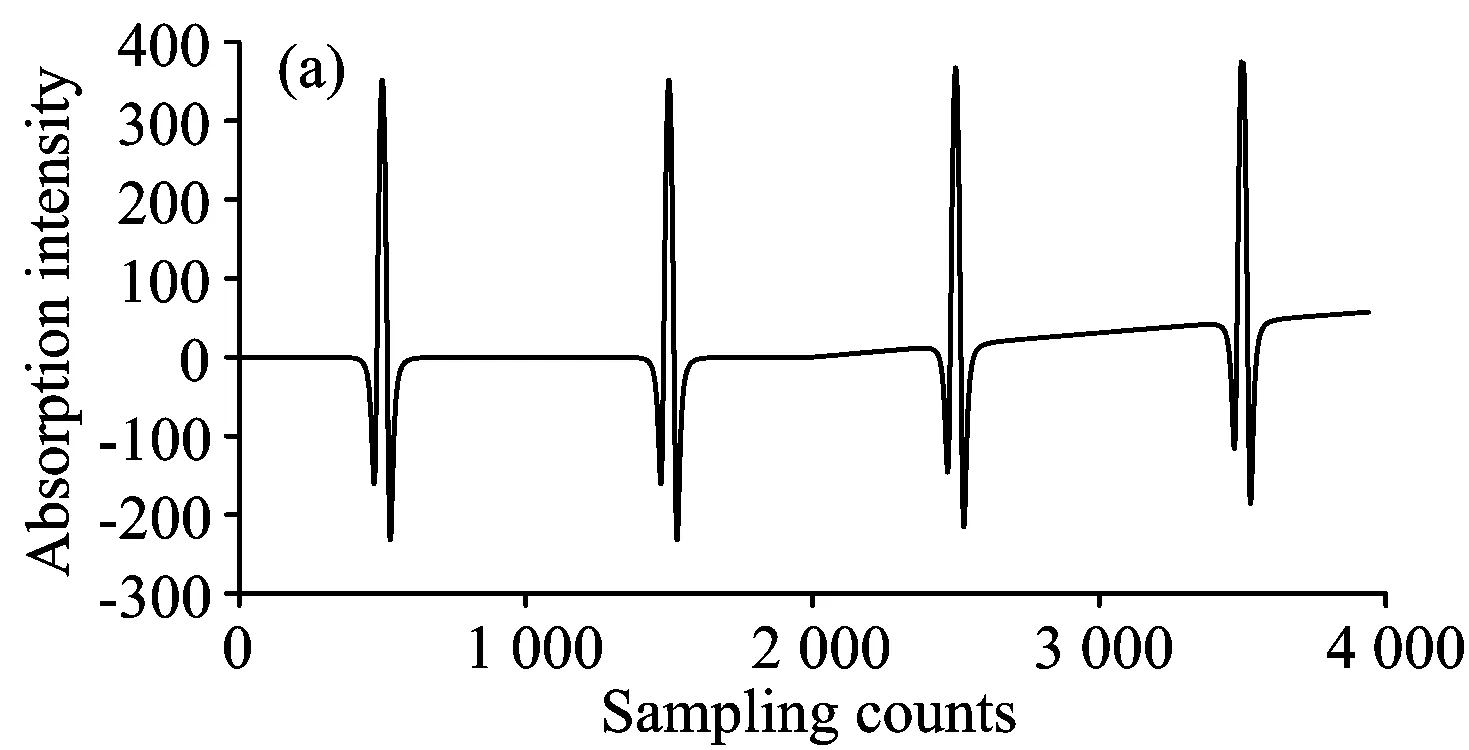
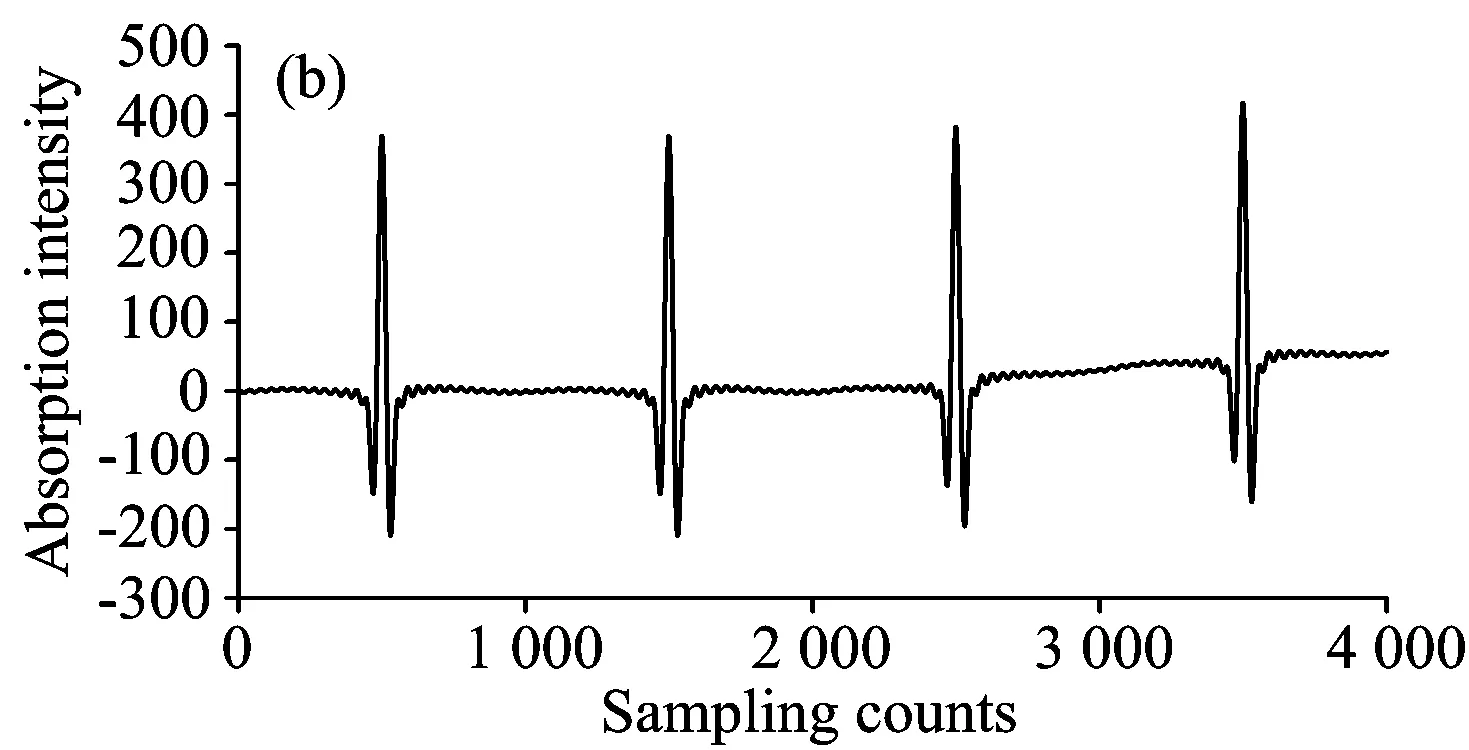


图6 构造hankel矩阵方法基线纠漂
3 平台实验及结果
实验平台主要由三个部分组成:光源及其驱动部分、光路及吸收气体池部分、探测接收和数据处理部分。其中光源及其驱动部分包括:信号发生器、激光驱动器、激光器。光路及吸收气体池部分包括:激光准直器、长光程气体池。探测接收和数据处理部分包括:光电探测器、前置放大器、锁相放大器、数据采集卡、计算机数据存储及处理模块。系统结构框图如图7所示。

图7 实验平台结构
实验时信号发生器产生5 Hz、0.5 V的正弦信号与30 kHz、0.2 V的锯齿波信号叠加成的调制信号。该调制信号被送入激光驱动器,由激光驱动器产生中心电流为50 mA的电流信号来驱动激光器,将激光器输出的1 510 nm激光进行调制。出射激光经过准直系统的调整后进入气体池,经待测气体吸收后,将携带待测气体吸收信号。实验采用体积比浓度为500×10-6的氨气进行测量。出射激光被光电探测器接收后转换为电信号,进入前置放大器、锁相放大器、数据采集与控制系统进行A/D转换以及后续处理。
图8(a)所示为采集的一段原始二次谐波信号,可以看到信号中包含小幅度的高频噪声和基线漂移。根据模拟实验的结论,连续截断信号的方法适于去除基线漂移,构造hankel矩阵的方法适于去除高频噪声。对于高频噪声和基线漂移均存在的二次谐波信号,经过两种方法构造矩阵进行两次奇异值分解与矩阵重构后得到图8(b),可以看到高频噪声和基线漂移都明显得到了去除。两次奇异值分解后的二次谐波最大波动幅度由19.3%降到1.5%,标准差由13.3%降到1.1%,系统噪声去除率达到80%。
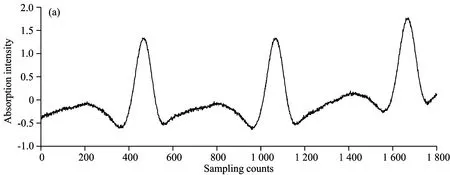

图8 TDLAS系统测量氨气浓度实验的二次谐波信号
4 结 论
将奇异值分解方法用于去除TDLAS系统的高频噪声和基线漂移,模拟实验发现不同构造矩阵的方法对不同系统噪声处理效果不同。去除高频噪声时,构造hankel矩阵的方法更优,噪声去除率达73%;而进行基线矫正时,连续截断信号构造矩阵的方法更优,对于基线漂移的去除率达78%。以测量体积比浓度为500×10-6的氨气为例,经过两种方法构造矩阵进行两次奇异值分解后,总的系统噪声去除率达到80%。因此,处理不同的系统噪声,要分别使用合适的方法构造矩阵进行奇异值分解,去噪和矫正后的二次谐波信号更有助于后续处理。
[1] ZHANG Zeng-fu, ZOU De-bao, CHEN Wen-liang, et al(张增福, 邹得宝, 陈文亮, 等). Journal of Optoelectronics· Laser(光电子· 激光), 2013, 12: 20.
[2] ZHANG Zhi-rong, SUN Peng-shuai, XIA Hua, et al(张志荣, 孙鹏帅, 夏 滑, 等). Acta Photonica Sinica(光子学报), 2015, 1: 7.
[3] TU Xing-hua, LIU Wen-qing, WANG Tie-dong, et al(涂兴华, 刘文清, 王铁栋, 等). Chinese Journal of Quantum Electronics(量子电子学报),2006,23(4):522.
[4] HU Ya-jun, ZHAO Xue-hong, ZHANG Rui, et al(胡雅君, 赵学玒, 张 锐, 等). Acta Optica Sinica(光学学报), 2013,(11): 288.
[5] HE Ying, ZHANG Yu-jun, WANG Li-ming, et al(何 莹, 张玉钧, 王立明, 等). Optical Technique(光学技术), 2012, 38(4): 421.
[6] PANG Tao, XIA Hua, WU Bian, et al(庞 涛, 夏 滑, 吴 边, 等). Journal of Optoelectronics· Laser(光电子·激光), 2015, 3: 27.
[7] ZHAO Xue-zhi, YE Bang-yan(赵学智, 叶邦彦). Acta Electronica Sinica(电子学报), 2008, 36(8): 1582.
[8] ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian(赵学智, 叶邦彦, 陈统坚). Journal of Vibration and Shock(振动与冲击), 2008, 27(6): 11.
[9] KANG Chun-yu, ZHANG Xin-hua(康春玉, 章新华). Technical Acoustics(声学技术), 2008, 27(3): 455.
[10] Bomse D S, Kane D J. Applied Physics B, 2006, 85(2-3): 461.
[11] Beattie J R, McGarvey J J. Journal of Raman Spectroscopy, 2013, 44(2): 329.
[12] Mappe-Fogaing I, Joly L, Durry G, et al. Applied Physics B, 2012, 108(4): 933.
[13] Huang Y F, Ueng H Y, Chung C R, et al. IEEE Journal of Quantum Electronics, 1999, 35(5): 757.
(Received Sep. 8, 2015; accepted Dec. 28, 2015)
*Corresponding author
A Singular Value Decomposition Method for Tunable Diode Laser Absorption Spectroscopy System to Remove Systematic Noises
WANG Zhe1, WANG Yan1, ZHANG Rui2, ZHAO Xue-hong1*, LIU Qiao-jun2, LI Cong-rong2
1. College of Precision Instrument and Opto-electronics Engineering, Tianjin University, Tianjin 300072, China
2. College of Electronic Information and Automation, Tianjin University of Science & Technology, Tianjin 300222, China
Detection of gas concentration with tunable diode laser absorption spectroscopy (TDLAS) techniques is affected by baseline drift and high-frequency noise. Therefore, how to remove the systematic noises has been a hot spot. This paper analyzes the significance of singular value decomposition (SVD) in TDLAS detection system with two different methods of constructing a matrix, and it discusses the differences of processing results for different noises. The second harmonic signal is arranged in a matrix and decomposed. We select the appropriate threshold and putthose singular values smaller than the threshold into zero, then reconstruct the matrix. Experiments show that SVD method does not require additional system components or pass into the zero gas to subtract background. This method is able to remove noises of TDLAS system quickly and effectively. We found that the method of constructing a hankel matrix is suitable for removing high-frequency noise. However, the method of constructing a continuous-cutoff-signal matrix is suitable for removing baseline drift. For example, we set up a TDLAS system to measure the concentration of NH3while the noise removal rate of the second harmonic curve is up to 80% with this method.
Singular value decomposition; Tunable diode laser absorption spectroscopy; Baseline correction; Denoising
2015-09-08,
2015-12-28
国家重点基础研究发展计划(2010CB327800)和天津市应用基础与前沿技术研究计划(14JCYBJC22800)资助
王 喆, 女,1990年生,天津大学精密仪器与光电子工程学院硕士研究生 e-mail: wangzhe1990@tju.edu.cn *通讯联系人 e-mail: zhaoxh@tju.edu.cn
TH744.1
A
10.3964/j.issn.1000-0593(2016)10-3369-08
- 光谱学与光谱分析的其它文章
- Gd靶激光等离子体光源离带辐射及其等离子体演化的研究
- Probing the Binding of Torasemide to Pepsin and Trypsin by Spectroscopic and Molecular Docking Methods
- Mn(Ⅱ)-5-Br-PADAP共沉淀-火焰原子吸收光谱法测定虾、贝样中的镉
- Near Infrared Spectroscopy Study on Nitrogen in Shortcut Nitrification and Denitrification Using Principal Component Analysis Combined with BP Neural Networks
- 内蒙古草原植被最大光能利用率取值优化研究
- 健康和糖尿病大鼠红细胞荧光光谱非线性程度差异

