基于有约束非负矩阵分解的原稿基色色料光谱预测方法
何颂华,陈 桥*,段 江
1. 深圳职业技术学院传播工程学院,广东 深圳 518055
2. 西南财经大学经济信息工程学院,四川 成都 610075
基于有约束非负矩阵分解的原稿基色色料光谱预测方法
何颂华1,陈 桥1*,段 江2
1. 深圳职业技术学院传播工程学院,广东 深圳 518055
2. 西南财经大学经济信息工程学院,四川 成都 610075
针对直接在光谱反射率空间,对原稿颜色样本光谱的主成分分析会导致特征向量的数目超过真实物理维度(原稿所用基色色料)的数量,以及特征向量和对应系数存在负值,不能直接表示原稿基色色料的光谱特性和对应浓度等情况。创新性的提出需根据原稿色料的光学特性建立一个完全线性的光谱空间,并在该空间中使用带约束条件的非负矩阵分解实现对原稿基色数量和光谱形状进行预测的方法。对此,首先设计了一个实现对原稿基色色料光谱预测方法的总体研究方案和实现步骤,再以透明色料原稿为例,研究如何选择和构建一个符合其光学特性的光谱线性空间,然后再在基本非负矩阵分解(BNMF)基础上提出针对基色色料光谱预测的有约束非负矩阵分解算法(SCNMF)。针对BNMF算法会出现多重最优解,为了提高预测精度,使矩阵分解结果有明确的物理意义,所提出的SCNMF算法需要满足4个约束条件:非负性约束;全加性约束;平滑性约束;稀疏性约束。建立了满足约束条件的目标函数和迭代算法。预测结果表明本文提出的新方法能有效的实现对原稿基色物理维度和基色色料光谱的准确预测。
基色色料光谱预测;光谱颜色复制;非负矩阵非解;线性混合空间;主成分分析
引 言
光谱颜色复制技术使用光谱数据编码即光谱反射率或透射率数据来描述颜色信息,因此可使同色异谱程度达到最小[1]。并且光谱颜色复制技术在对颜色光谱进行重建时必须采用多基色成色方式,这就大大增加了颜色叠加的自由度,扩大了颜色再现的范围,因此特别适用于高保真颜色复制[2-3]。要实现对原稿的光谱颜色复制,首先必需确定一组基色色料,以在多光谱空间中进行原稿色彩的表示与再现。这组基色色料的成功确定必须包括两个方面:对基色物理维度的估计,即确定原稿颜色是由几种基色色料合成得到;对基色色料光谱的估计。目前,用于基色色料光谱预测的方法不多,主要有基本主成分分析法PCA[4-8],以及Tzeng提出的基于旋转主成分分析的光谱预测方法[9]。将PCA法用于光谱特征分析时,会出现特征向量和其对应权重系数出现负值,因而在物理上没有任何意义的情况;基于旋转主成分分析的光谱估计方法预测精度取决于旋转初值的选取,具有很大的不确定性和不准确性。本研究将结合非负矩阵分解提出一种新的基色色料预测技术,可较为精确的实现对透明色料原稿基色物理维度和色料光谱的估计。
1 原稿基色色料光谱预测方法的总体研究方案设计
基于有约束非负矩阵分解的原稿基色色料光谱预测方法将完全摒弃由主成分分析所建立的特征向量,而是根据非负矩阵分解局部特征构成整体的思想,直接对非负的光谱数据集进行矩阵分解,并进行非负性约束和其他条件约束,分解得到的结果基向量不存在负值,在实际应用中具有明确物理意义,并具有纯加性的特点。由于在光谱反射率空间,主成分分析得到的显著维度超出了实际物理维度[9],因此该方法必须首先要将光谱反射率空间转换到一个能反映实际物理维度的线性混合空间,并在这个线性混合空间中进行有约束非负矩阵分解。
基于有约束非负矩阵分解的原稿基色色料光谱预测方法的总体研究方案如图1所示。
在该研究方案中最为关键的三步为色料光谱线性模型建立、针对原稿色料光学特性建立线性混合空间并在该空间进行有约束非负矩阵分解预测原稿色料光谱。为了对色料光谱预测结果进行验证,在本研究方案中还设计了预测光谱与实际基色色料光谱的评价方法。
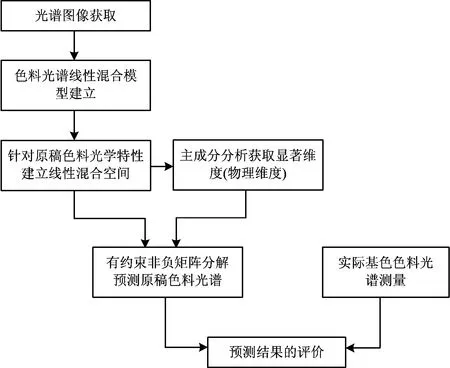
图1 基于有约束非负矩阵分解的原稿基色色料光谱预测方法的总体研究方案
Fig.1 Spectral prediction research program for original primary pigments based on constraint NMF
2 色料线性混合模型和线性混合空间建立
不同原稿其色料混合的光学特性不一样,因此在建立原稿色料线性混合空间时应充分考虑原稿色料的光学特性。本研究以透明色料原稿为例来分析其色料性线混合模型和线性混合空间的建立。kubleka-munk混介理论给了一个很好的启发,即可以通过各色料吸收系数和散射系数与色料浓度加权后的线性相加得到混合后的吸收系数和散射系数。但大量的研究文献已表明对于不透明和半透明色料,其色料浓度与吸收系数和散射系数并不是一种线性关系[10]。
对于透明色料原稿来说,由于色料完全透明,并附着在一高反射基底上的原稿,如相纸,其各色剂层的散射系数s近似为0,只有吸收系数k。因此透明色料相对于不透明和半透明色料其光学特性能较多的符合Kubleka-Munk模型的假设条件,则多种透明色料混合后的吸收系数可以由参与混合的各色料浓度线性表示,即满足
(1)
且在式(1)中各色料浓度之和为1,这样对于透明色料,光谱吸收系数空间就是一个完全线性的混合空间。
3 用于基色色料光谱预测的约束非负矩阵分解算法(SCNMF)
在确定线性混合空间后,就可以直接利用所提出的光谱约束非负矩阵算法(spectra constrained non-negative matrix factorization algorithm,SCNMF)进行基色数量和基色光谱的预测。为了算法的通用性,这里用Ψλ表示线性的光谱空间。
3.1 约束条件的确定
由于本研究方案是直接对线性空间Ψλ的光谱数据进行矩阵分解以估计基色色料光谱和(浓度)混合百分比,为使分解的结果有明确的物理意义,首先必须保证矩阵分解时满足约束条件:
(1)非负性约束,基色色料光谱和(浓度)混合百分比不可能为负值;
(2)全加性约束,本改进算法由于基于式(1)所建立的色料混合线性模型,该线性混合模型对各色料(浓度)混合百分比除了非负的约束外还有全加性约束,即要求任意像素其混合色料的各浓度百分比之和为1。
利用最优化技术可归结为求解下面的问题
(2)
(3)
(4)
(5)
其中,p为Ψλ空间进行主成分分析得到的显著维数,反映参与混合的基色色料数量。Ψλ, p为预测的光谱值,Ψλ为需要验证目标的光谱值,F是最小化目标函数。式(4)和式(5)为约束条件。
上面的最优化问题正好与非负矩阵分解算法思想相一致,对比于基本非负矩阵分解算法,其约束优化条件多个一个全加性约束,该约束条件可在非负矩阵分解的迭代过程中加入。采用文献[11]所使用的表示形式,具体做法是引入新的矩阵ψs和Ψs
(6)
其中1T表示一个向量的所有分量都为1,即1=(1,1,…,1)T,δ为权值,控制总和为1这一约束条件对目标函数的影响。用ψs和Ψs替代ψ和Ψ进行算法的迭代,并在每次迭代完ψ之后,从ψs和Ψs中取出原本属于ψ和Ψ的部分,并重新进行一次式(6)的扩展即可。这样在算法收敛时同时也能进行全加性和为一的约束。
对于基色色料光谱的物理意义除了满足约束条件(1)和(2)外,这里还应该考虑到色料光谱自身特点和色料分布特点,需要增加约束条件(3)和(4):
(3)平滑性约束(smoothness constraint),色料来自于自然界或人工提取,其光谱本身具有平滑性,曲线形状变化平缓,一般不存在窄带光谱;
(4)稀疏性约束(sparseness constraint),所谓稀疏性是指因为在一般情况下,任何基色色料的(浓度)混合百分比分布都不会充满整个图像空间,混合色料中包含的只是几种基色色料,而不是所有基色色料。即每种基色色料的混合百分比只是分布于空间中的部分区域,具有一定的稀疏度。对于非负矩阵分解来说,其中一个矩阵的稀疏性必然导致另一个矩阵是非稀疏性(或称平滑性),使得最终的乘积能够更好的拟合观测信号。这一点恰好加强了约束条件(3)色料光谱的平滑性特征。
3.2 SCNMF目标函数和迭代公式
由于平滑性约束和稀疏性约束是针对非负基色色料光谱矩阵ψ和浓度百分比矩阵C本身数据分布的约束,一般都是通过对非负矩阵目标函数引入惩罚项来约束矩阵ψ和C[12]。在非负矩阵分解的两种目标函数中,欧氏距离最为直观,应用最为广泛,由于色料光谱预测的物理意义与欧氏距离比较符合,故以欧氏距离的情况下进行算法推导。加入惩罚项后,目标函数由式(7)变为式(8)的形式
(7)
(8)
其中,‖‖F代表矩阵的Frobenius范数,当且仅当R=WH时,函数取得最小值。式(8)中,aJ1(ψ)和βJ2(C)是依赖于应用的惩罚项,a和β是规则化参数,它们平衡着逼近误差和约束之间的消长关系。对于色料光谱矩阵的平滑性约束和浓度百分比矩阵的稀疏性约束,引入惩罚项见式(9)
(9)
这样修改的目标函数为
(10)
在进行算法迭代时,采用基本非负矩阵算法(basic non-negative matrix factorization algorithm,BNMF)的乘性迭代规则,目标函数式(10)是单调非增的。为满足全加性限制,迭代时分别用ψe和Ψe替代ψ和Ψ,其迭代公式为
(11)
(12)
ψe和C的梯度为
(13)
(14)
将式(13)和式(14)代入式(11)和式(12)中,得
(15)
(16)
定义迭代步长
(17)
(18)
将式(17)和式(18)代入式(15)和式(16)之后可得到乘性迭代式(19)和式(20)
(19)
(20)
由于BNMF的解不具有唯一性,即它存在多重最优解,这显然与色料光谱预测的唯一性相矛盾,为了解决解的非唯一性问题,可通过合理的构建目标函数,对分解结果增加除了非负性外的其他更多条件限制,因而提出的SCNMF算法针对基色色料光谱的自身特点和分布特点,在解的结果为非负性的基础上增加了全加性约束、平滑性约束、稀疏性约束,将从理论上更容易找到全局最优解,增强基色色料光谱预测的准确性。
4 结果与讨论
实验中将对kodak Q60C的IT8.7/2反射色标(图2)进行实验验证,该色标介质是相纸,相纸是由一高反射不透明基底加上三种透明染料层(C,M,Y)制得的,因此已知各颜色块呈色是通过三种透明染料合成得到。首先使用Gretag spectraeye测量色标的光谱反射率,并将其转换到吸收系数K空间,再在这两个空间分别进行PCA分析。
图2 kodak Q60C的IT8.7/2反射色标
表1是分别在光谱反射率空间和吸收系数空间用PCA得到的前六个特征向量重构光谱的贡献率比较。可明显看出,在光谱反射率空间使用6个特征向量进行光谱重构时,累积贡献率达到99.85%,而在吸收系数空间只需要使用3个特征向量进行光谱重构,累积贡献率就达到99.95%,在使用5个特征向量重构时,累积贡献率接近100%。因为累积贡献率反映了多个特征向量对信息的贡献程度,将累积贡献率增加到99%以上并且增长速度不再明显变化时的特征向量数目确定为基色染料混合的物理维度,因此在吸收系数空间中可确定染料混合的物理维度为3,与实际情况相吻合。
表1 光谱反射率空间和吸收系数空间特征向量贡献率比较
Table 1 The percent variance in both reflectance and absorption space of IT8.7/2 refflection target
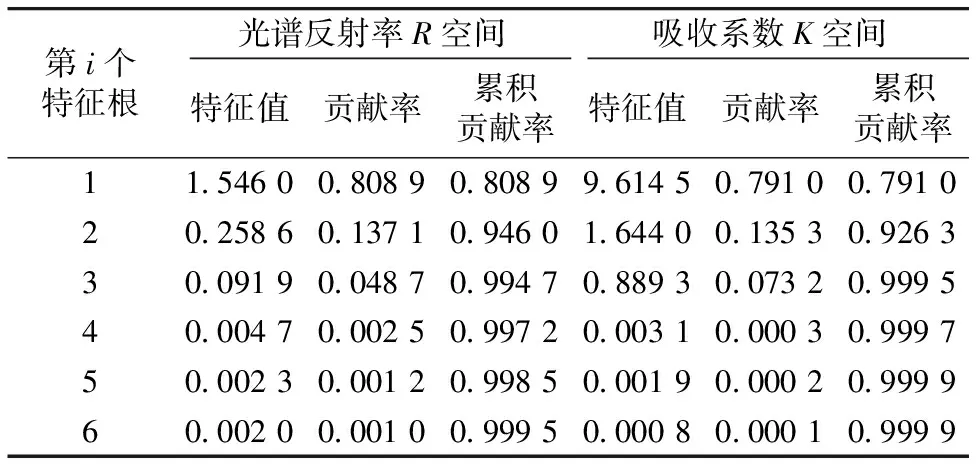
第i个特征根光谱反射率R空间吸收系数K空间特征值贡献率累积贡献率特征值贡献率累积贡献率11 54600 80890 80899 61450 79100 791020 25860 13710 94601 64400 13530 926330 09190 04870 99470 88930 07320 999540 00470 00250 99720 00310 00030 999750 00230 00120 99850 00190 00020 999960 00200 00100 99950 00080 00010 9999
接下来再分析在两个空间进行光谱重构时光谱重构精度和色度精度的表现。评价光谱重构精度使用均方根误差sRMS,评价色度精度使用CIELAB ΔE*ab色差公式,计算色差时采用D50标准光源和CIE1931 2度视场的颜色匹配函数。同样发现,在吸收系数空间,通过三个特征向量重构后的光谱精度和色差都远好于在光谱反射率空间通过五个特征向量重构的光谱。
从表2和表3中都可看出,在吸收系数空间只需要三个特征向量进行光谱重构后,其sRMS与反射率空间使用六个特征向量的sRMS接近,但其色差的最小值、最大值、平均值都要好于在反射率空间使用六个特征向量进行光谱重构后表现。
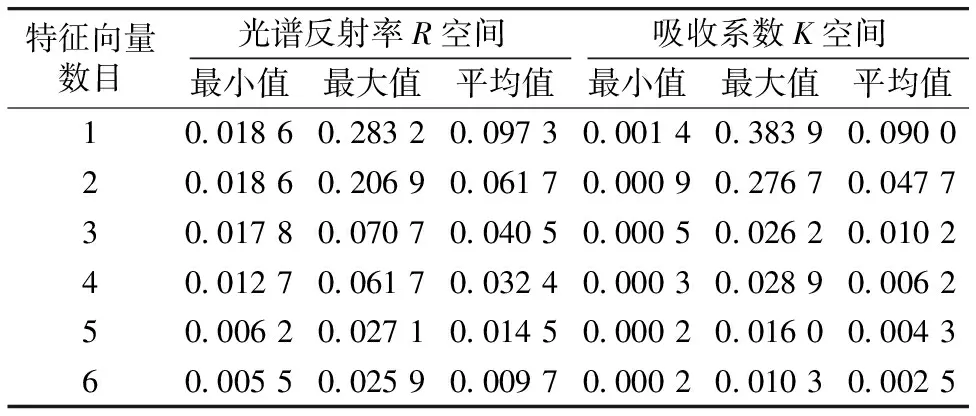
表2 在光谱反射率空间和吸收系数空间进行光谱重构后sRMS比较
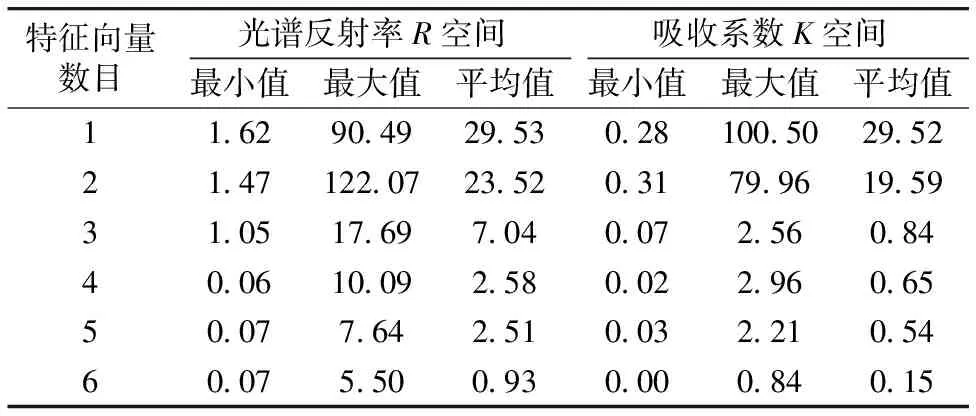
表3 在光谱反射率空间和吸收系数空间进行光谱重构后色差比较
从两个空间的特征向量累积贡献率、光谱精度和色度精度的比较分析可得出,将光谱值从反射率空间转化到吸收系数空间后,需要的特征向量将大为减少。而已知kodak Q60C的IT8.7/2色标本身是用相纸制得的,因此各颜色块呈色是通过三种染料合成得到,其色料混合的线性空间当然是三维的,但如果单从光谱反射率空间通过分析特征向量的方式寻找物理色料的数目,表1证明其结果与实际不符合,但如果将光谱值从反射率空间转到吸收系数空间,会发现进行重构的特征向量的数量正好与实际物理色料的数量一致。
由以上分析可知对于透明色料连续调原稿,吸收系数空间可作为色料混合的线性空间,并通过主成份分析确定物理色料数为3,从而明确了在吸收系数空间中进行SCNMF算法需要分解的基向量个数为3。图3为在吸收系数空间中采用SCNMF算法对基色色料吸收光谱的估计,其预测结果与该相纸实际所用的色料光谱曲线形状非常接近。在使用SCNMF算法进行平滑性限制时α=0.1,β=0,最后的量化结果是通过取6次实验的平均值得到的。

图3 吸收系数空间中对kodak Q60C的IT8.7/2 色标透明色料光谱的预测
Table 4 Similarity degree between estimated spectrum and real spectrum of IT8.7/2 in absorption space
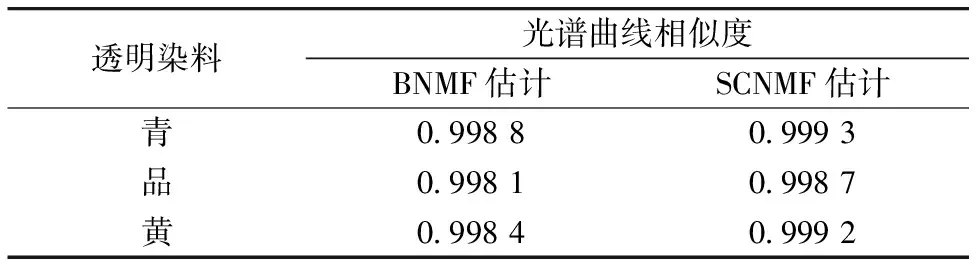
透明染料光谱曲线相似度BNMF估计SCNMF估计青0 99880 9993品0 99810 9987黄0 99840 9992
由于预测光谱与实际光谱在比较时进行了归一化,因此不能通过均方根方根误差等评价方式判断预测精度,这里本研究中通过矢量相关分析比较两者之间的相似度。相关系数越接近于1,预测光谱与实际光谱越相似。对相关系数的计算可利用matlab的corrcoef函数,三种透明染料在吸收系数空间中预测光谱与实际光谱的曲线相似度见表4。表中的数据比较也表明通过SCNMF算法预测的结果要好于BNMF算法预测的结果。
5 结 论
针对本研究提出的有约束非负矩阵分解的原稿基色色料光谱预测方法得出以下结论:
(1)不同原稿其色料混合的光学特性不一样,因此在建立原稿色料线性混合空间时应充分考虑原稿色料的光学特性。对于透明色料连续调原稿选用吸收系数空间作为线性混合空间,该空间是完全线性的。
(2)在对色料混合的物理维度判断上,可将累积贡献率增加到99%以上并且增长速度不再明显变化时的特征向量数目确定为基色染料混合的物理维度,但该判断的前提条件是所建立的线性混合空间是一个能真实反映色料混合的完全线性空间。
(3)为了提高预测精度,使矩阵分解结果有明确的物理意义,所提出的SCNMF算法需要满足4个约束条件:非负性约束、全加性约束、平滑性约束、稀疏性约束。
(4)在评价预测光谱的预测精度时,由于对预测光谱进行了归一化,因此不能通过均方根方根误差等评价方式判断预测精度,可通过矢量相关分析比较预测光谱与实际光谱之间的相似度。相关系数越接近于1,预测光谱与实际光谱越相似。
[1] HE Song-hua, CHEN Qiao, DUAN Jiang(何颂华, 陈 桥, 段 江). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2015, 35(6): 1459.
[2] KONG Ling-wang, ZHU Yuan-hong, LI Qiong(孔令罔, 朱元泓, 李 琼, 等). Geomatics and Information Science of Wuhan University(武汉大学学报·信息科学版), 2006, 31(9): 788.
[3] WANG Ying, ZENG Ping, WANG Yi-feng(王 莹,曾 平,王义峰). Acta Optica Sinica(光学学报), 2009, 29(8): 2122.
[4] LI Jin-cheng, LIU Zhen, CHEN Guang-xue(李金城, 刘 真, 陈广学). Acta Optica Sinica(光学学报), 2009, 29(8): 2122.
[5] Xu Dongbo, Wang Xiangzhao, Bu Yang. Chinese Optics Letters, 2012, 10(12): 121202-1.
[6] XU Fa-qiang, WAN Xiao-xia, ZHU Yuan-hong(许法强, 万晓霞, 朱元泓). Optics and Precision Engineering(光学 精密工程), 2008, 16(3): 518.
[7] HE Song-hua, LIU Zhen, CHEN Qiao(何颂华, 刘 真, 陈 桥). Acta Optica Sinica(光学学报), 2014, 34(2): 0233001-1.
[8] Wang Ying, Zeng Ping, Luo Xuemei, et al. Journal of Southeast University·English Edition, 2013, 2(4): 486.
[9] Tzeng D Y, Berns R S. Color Research and Application, 2005, 30(2): 84.
[10] He Songhua, Liu Zhen. Procedia Engineering, 2011, 23: 320.
[11] Heinz D C, Chang C I. IEEE Geoscience and Remote Sensing Letters, 2001, 39(3): 529.
[12] Lee D, Seung H. Nature, 1999, 401: 788.
(Received Aug. 3, 2015; accepted Nov. 16, 2015)
*Corresponding author
The Spectral Prediction of Original Primary Pigment Based on Constrained Non-Negative Matrix Factorization
HE Song-hua1,CHEN Qiao1*,DUAN Jiang2
1. School of Communication, Shenzhen Polytechnic, Shenzhen 518055, China
2. Computer Science Department of Southwestern University of Finance and Economics, Chengdu 610075, China
With direct prediction in the spectral reflectance space with principal component analysis, the numbers of eigenvectors will surpass the numbers of real primary pigments while the eigenvectors and the corresponding coefficients have negative value, which can not directly presented original primary pigment spectral characteristics and corresponding concentration. We proposed an innovative spectral prediction method in which a complete linear spectral space was created according to optical properties of originals pigment. A constrained non-negative matrix factorization algorithm to predict the numbers and spectral curve shapes of real primary pigments was used in the space. So, this paper designed an overall research plan and implementation process about spectral prediction method firstly, and studied how to select and establish a spectral linear space which was conformed to optical properties of originals; taking transparent pigments as example, and spectra constrained non-negative matrix factorization (SCNMF) algorithm was established to predict primary pigment spectra based on basic non-negative matrix factorization algorithm (BNMF). Aiming at realizing multiple optimal solution of BNMF and improving the prediction accuracy as well as make the matrix decomposition results to be clearly physically meaningful; the proposed SCNMF needs to satisfy four constraints: non negative constraint, additive constraint, smoothness constraint and sparseness constraint. The objective function and iterative algorithm to meet four constraints were set up. The prediction results show that the proposed method can realize accurate prediction of original primary pigments’ numbers and spectra effectively.
Spectral estimation of primary pigments; Spectral color reproduction; Non-negative matrix factorization; Linear mixing space; Principal component analysis
2015-08-03,
2015-11-16
国家自然科学基金项目(61108087),四川省杰出青年学术技术带头人资助计划项目(2012jq0017)资助
何颂华,1977年生,深圳职业技术学院教授 e-mail: hdh1818@szpt.edu.cn *通讯联系人 e-mail: qiaochen@szpt.edu.cn
TP391.4; O432.3
A
10.3964/j.issn.1000-0593(2016)10-3274-06
- 光谱学与光谱分析的其它文章
- Gd靶激光等离子体光源离带辐射及其等离子体演化的研究
- Probing the Binding of Torasemide to Pepsin and Trypsin by Spectroscopic and Molecular Docking Methods
- Mn(Ⅱ)-5-Br-PADAP共沉淀-火焰原子吸收光谱法测定虾、贝样中的镉
- Near Infrared Spectroscopy Study on Nitrogen in Shortcut Nitrification and Denitrification Using Principal Component Analysis Combined with BP Neural Networks
- 内蒙古草原植被最大光能利用率取值优化研究
- 健康和糖尿病大鼠红细胞荧光光谱非线性程度差异

