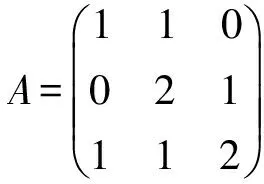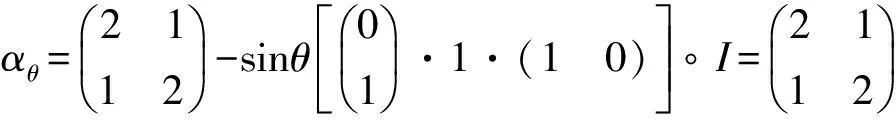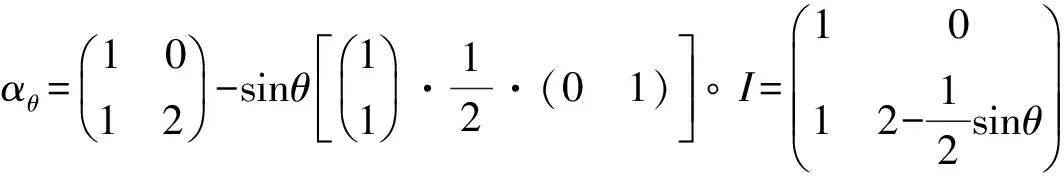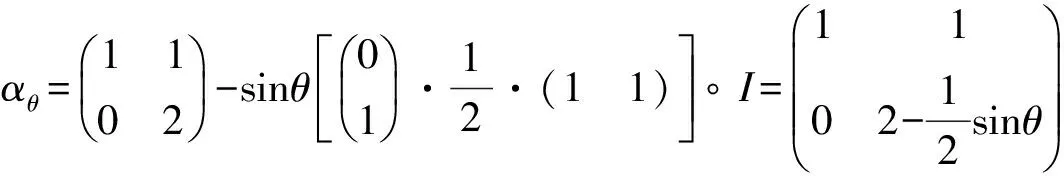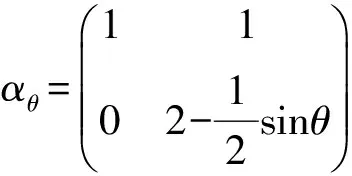双严格积γ-对角占优矩阵的三角-schur补
常萌萌,李华慧
(安阳学院,河南 安阳,455000)
双严格积γ-对角占优矩阵的三角-schur补
常萌萌,李华慧
(安阳学院,河南 安阳,455000)
为了进一步研究矩阵Schur 补的性质,引入三角-schur补的概念(当θ=π/2时三角-schur补即为对角-schur补),证明了双严格积γ-对角占优矩阵的三角-schur补仍然是双严格积γ-对角占优矩阵,并用数值例子对结论进行了验证。
三角-schur补;双严格积γ-对角占优矩阵;矩阵
矩阵 Schur 补的概念最早由数学家 Issai Schur 提出。随后,许多学者对其进行深入研究并取得了很多非常有意义的结果。对于一类特殊的矩阵,人们总是关注其子矩阵或与子矩阵有关的矩阵是否具有原矩阵的某些性质。Liu等[1~3]证明了严格双对角占优,广义严格双对角占优,严格γ-对角占优矩阵和严格积γ-对角占优矩阵的Schur补仍然是严格双对角占优,广义严格双对角占优,严格γ-对角占优矩阵和严格积γ-对角占优矩阵。赵云平[4,5]证明了双严格γ-对角占优矩阵,双严格积γ-对角占优矩阵的对角-schur补仍然是双严格γ-对角占优矩阵,双严格积γ-对角占优矩阵。常萌萌[6]和梅晓凤等[7]、李丽梅等[8]引入了三角-schur补的概念,证明了严格对角占优矩阵,严格双对角占优矩阵,严格γ-对角占优矩阵和严格积γ-对角占优矩阵的三角-schur补仍然是严格对角占优矩阵,严格双对角占优矩阵,严格γ-对角占优矩阵和严格积γ-对角占优矩阵。笔者在以上研究的基础上,期望证明双严格积γ-对角占优矩阵的三角-schur补仍然是双严格积γ-对角占优矩阵,并用数值例子对结论进行验证。
1 预备知识
为了表述方便,在此引入以下符号及定义。
Cn×n表示所有n×n阶复矩阵的集合,Rn×n表示所有n×n阶实矩阵的集合,I是单位矩阵。用α表示N={1,2,3,…,n}的一个子集且|α| 设A=(aij), B=(bij)∈Cn×n是2个矩阵,A∘B=(aij×bij)n×n称为矩阵A和B的Hadmard积。 显然A∘B∈Cn×n。 定义1[1]设A=(αij), α是N的一个子集且A(α)是一个非奇异矩阵,称 为矩阵A对应于A(α)的Schur补,记为A/A(α)或A/α。 定义2[3]设A=(αij),α是N的一个子集且A(α)是一个非奇异矩阵,称 为矩阵A对应于A(α)的对角-schur补,记为A/∘A(α)或A/∘α。 定义3 设A=(αij),α是N的一个子集且A(α)是一个非奇异矩阵,称 为矩阵A对应于A(α)的三角-schur补,记为A/∘A(α)θ或A/∘αθ。 定义4[10]设A=(aij)∈Rn×n,aii>0,aij≤0(∀i,j,i≠j),则称A是L-阵。 定义5[10]设A=(aij)∈Rn×n,若A=sI-B,B为非负矩阵,s>ρ(B),则称A为非奇异M-矩阵,其中ρ(B)为矩阵B的谱半径。 定义6[9]设A=(aij)∈Cn×n,若μ(A)=(μij)∈Rn×n,i,j=1,2,…,n,其中 则称μ(A)为A的比较矩阵。 定义7[9]设矩阵A=(aij)∈Cn×n,若A的比较矩阵μ(A)是非奇异M-矩阵,则称A为非奇异的H-矩阵,简称H-矩阵。 定义8[5]设矩阵A=(aij)∈Cn×n,若存在γ∈[0,1]使得对所有i,j∈N+,i≠j有 引理3[6]设A=(aij)∈Cn×n,定义矩阵AR=(aR)ij,其中 若AR是H-矩阵,Reaitjt>0(t=1,2,…,l),Reaiuju<0(u=1,2,…,m), l+m=n,则A有l个实部为正的特征值及m个实部为负的特征值。 定理1 若A=(aij)∈Cn×n是双严格积γ-对角占优矩阵,α⊂N,那么A的三角-schur补A/∘A(α)θ也是双严格积γ-对角占优矩阵。 证明 假设α={i1,i2,…,ik},α′={j1,j2,…,jl},k+l=n。 其中, 对于∀p,m∈{1,2,…,l},p≠m,有 其中, 其中 (2)又对q=p,m,∀s∈{1,2,…,k},有 其中 (3)对∀u,v∈{1,2,…,k},u≠v,有 |a11|=1,|a22|=2,|a33|=2, h1(A)=1,h2(A)=1,h3(A)=2,l1(A)=1,l2(A)=2,l3(A)=1。 则有 因此A为双严格积γ-对角占优矩阵。 下面验证A/∘A(α)θ也是双严格积γ-对角占优矩阵。 h1(A)=1,h2(A)=1,l1(A)=1,l2(A)=1 h1(A)=0,h2(A)=1,l1(A)=1,l2(A)=0 h1(A)=1,h2(A)=0,l1(A)=0,l2(A)=1 因此A/∘A(α)θ也是双严格积γ-对角占优矩阵。 [1] Liu Jianzhou,Zhang Juan,Liu Yu.The Schur complements of strictly doubly diagonally dominant matrices and its application[J].Linear Algebra and its Application,2012,437:168-183. [2] Liu Jianzhou,Huang Yunqing,Zhang Fuzhen.The Schur complements of generalized doubly diagonally dominant matrices[J].Linear Algebra and its Applications,2004,378:231-244. [3] Liu Jianzhou,Huang Zejun.The Schur complements ofγ-diagonally and productγ-diagonally dominant matrix and their disc separation[J].Linear Algebra and its Applications,2010,432:1 090-1 104. [4] 赵云平.双严格γ-对角占优矩阵的对角schur补[J].齐齐哈尔大学学报,2015,31(1):53-56,81. [5] 赵云平.双严格积γ-对角占优矩阵的对角Schur补[J].宁夏大学学报(自然科学版),2015,36(4):325-330. [6] 常萌萌.三类广义对角占优矩阵逆的数值特征[D].西安:陕西师范大学,2013:13-21. [7] 李丽梅,畅大为,梅晓凤.严格γ-对角占优矩阵的三角-schur补[J].纺织高校基础科学学报,2014,27(4):477-481. [8] 梅晓凤,畅大为,李丽梅.严格积γ-对角占优矩阵的三角-schur补[J].纺织高校基础科学学报,2014,27(4):482-486. [9] Horn R A,Johnson C R.Topics in matrix analysis[M].Cambridge:Cambridge University Press,1991. [10] 胡家赣.线性代数方程组的迭代解法[M].北京:科学出版社,1991. (责任编辑:朱宝昌) Triangle-schur Complements of Doubly Strictly Productγ-diagonally Dominant Matrices CHANG Mengmeng, LI Huahui (Anyang University, Anyang Henan,455000,China) In order to further study the properties of Schur complements, the concept of triangle-schur complements was introduced (whenθ=π/2, then triangle Schur-complements meant diagonal-schur complements). The triangle-schur complements of doubly strictly productγ-diagonally dominant matrix was proved to be a doubly strictly productγ-diagonally dominant matrix. At the same time, a numerical example was shown to illustrate the effectiveness of the criteria. triangle-schur complement; doubly strictly productγ-diagonally dominant matrices; H-matrix 10.3969/J.ISSN.1672-7983.2016.03.003 2016-08-24 O151.21 A 1672-7983(2016)03-0016-05 常萌萌(1988-),女,硕士,讲师。主要研究方向:数值线性代数。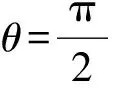



2 主要结论及证明
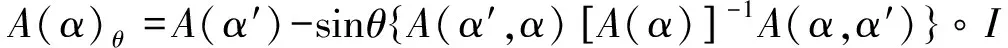


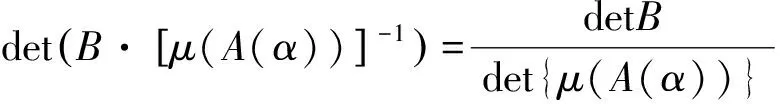
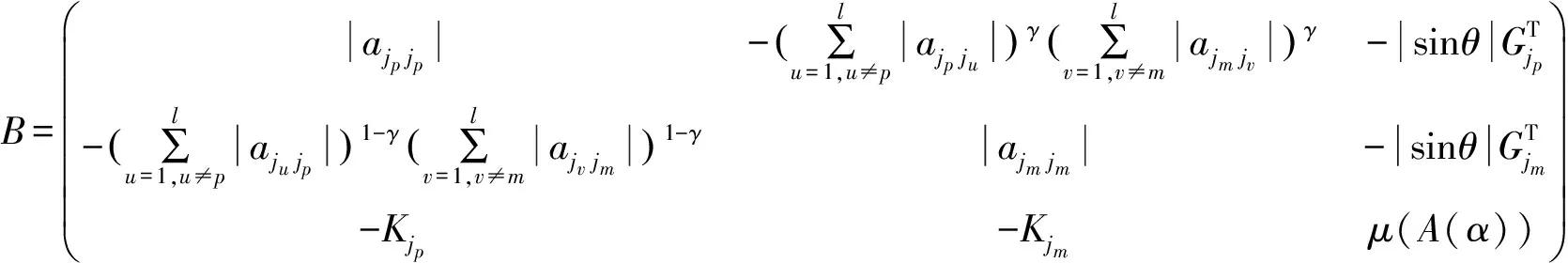
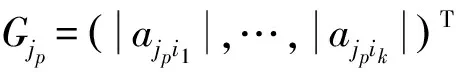
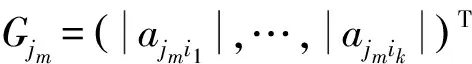
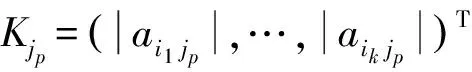
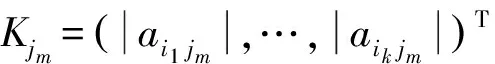
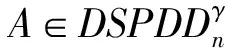
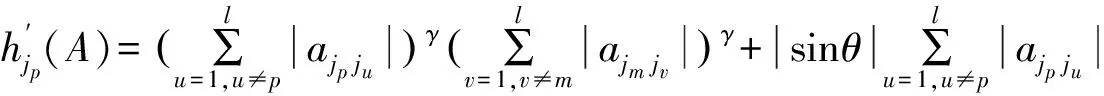

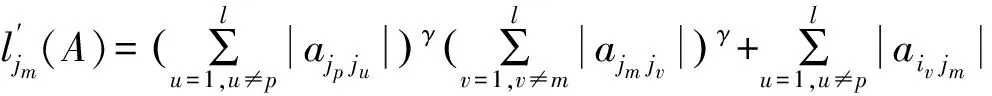




3 数值例子