用于风场探测的非对称空间外差干涉数据处理方法研究

沈 静，熊 伟*，施海亮，李志伟，胡广骁，乔延利

1.中国科学院合肥物质科学研究院安徽光机所，安徽 合肥 230031 2.中国科学技术大学，安徽 合肥 230026 3.中国科学院通用光学定标与表征技术重点实验，安徽 合肥 230031

用于风场探测的非对称空间外差干涉数据处理方法研究

沈 静1, 2, 3，熊 伟1, 2, 3*，施海亮1, 3，李志伟1, 3，胡广骁1, 3，乔延利1, 3

1.中国科学院合肥物质科学研究院安徽光机所，安徽 合肥 230031 2.中国科学技术大学，安徽 合肥 230026 3.中国科学院通用光学定标与表征技术重点实验，安徽 合肥 230031

利用非对称空间外差光谱技术和多普勒效应，通过测量中高层大气气辉谱线的干涉图，采用傅里叶变换的方法求解相位，获得大气的风速信息。分析了干涉数据的处理方法，并针对干涉相位的求解进行推导。相比于传统观空间外差数据处理，不仅要考虑噪声和系统误差，而且要考虑用于光谱隔离的窗函数引入的相位误差。通过软件模拟了窗函数的类型和窗长度对干涉数据和风速误差曲线的影响；在此基础上选择合适的窗函数模拟了对干涉图添加噪声和平场因子情况下的风速反演误差。结果说明，虽然窗函数造成了干涉图和相位的畸变，但是使用汉宁窗在合适的光程差处能够使其引入的误差低于5%；同时，噪声的仿真说明，风速误差随着系统噪声的增加而增大，在实验过程中控制噪声以及实验数据预处理对于控制风速精度的必要性。数据处理方法的研究和相关的仿真，对于提高空间外差风速测量精度及系统设计提供了理论参考，具有一定的指导意义。

风场探测；非对称空间外差光谱仪；干涉图；傅里叶变换；窗函数；噪声

引 言

中高层大气对全球气候与环境、大气物理、航天和军事研究意义深远，越来越受到人们的关注。大气风场不仅是该区域动力学和光化学过程的关键因素，对能量、动量与大气成分的传输起着巨大作用[1]，除此之外还是重要的空间环境参量，对航天器的运行轨道和安全产生很大的影响。因此，研究大气风场成为获取大气行为的重要方法。

多普勒非对称空间外差光谱技术(Doppler asymmetric spatial heterodyne spectroscopy, DASH)作为新兴的被动式风场探测手段成为近些年的研究热点[2-4]。该技术衍生于90年代的空间外差光谱技术(spatial heterodyne spectroscopy, SHS)，2006年由Harlander等提出，综合空间干涉与光栅衍射于一体，不仅继承了传统迈克尔逊干涉光谱仪的优点，避免了运动部件和窄带滤波，而且能够同时测量多个谱线，具有较强的空间环境适应性[5-6]。

空间外差光谱技术和迈克尔逊干涉技术皆以干涉图相位的变化解析大气风速，但是两种技术的实现过程不同。迈克尔逊风场测量通过四强度法计算相位，进而求得视线方向的风速[1]。非对称空间外差风场测量则通过光谱的逆变换，由干涉图的实虚部比求出光程差范围内每个点的相位，最终得到风速[6]。

DASH的数据处理过程相应较为复杂，在分析采样干涉图时，探测器的噪声和干涉系统的平场效应对干涉图和相位的影响非常显著[6-7]。除此之外，由于隔离特征谱时，窗函数的加入也使复原干涉图和相位产生明显失真。基于这点考虑，本文从DASH技术的基本原理出发，分析了干涉数据的处理方法，包括预处理和干涉相位求解。在求解干涉相位时，又针对窗函数的选择进行了分析。用Matlab软件模拟了窗函数的类型和有效长度对干涉数据和风速误差的影响，另外，对添加噪声和平场因子的干涉图进行模拟并计算相应的风速误差曲线。本研究对于研制新型风场探测仪器以及数据处理具有重要的理论意义。

1 DASH基本原理

基于DASH技术的干涉仪光学原理如图1所示[6]。

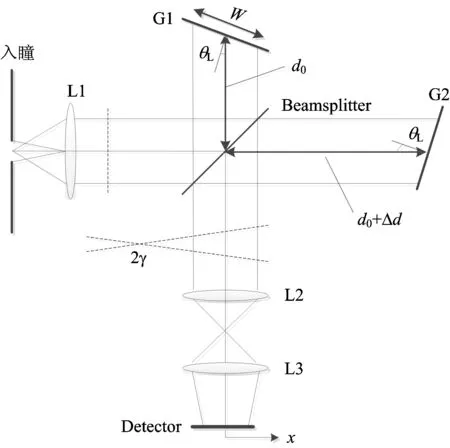
图1 DASH干涉仪的原理图

由衍射光栅G1和G2代替迈克尔逊干涉仪的平面反射镜，来自光源的光准直后入射到分束器，经过分束面透射和反射形成等强度的两束光到达光栅面G2和G2。受到光栅衍射的两束光在分束面会聚，形成菲索干涉条纹，最终成像于探测器。被探测器记录下的干涉图表示为

L=4xtanθL+2Δd

(1)

式(1)中，B(σ)是入射谱密度，σL是系统基频波数，L表示干涉光程差，x是探测器的位置坐标，Δd是一臂的偏置量，θL是光栅的Littrow角。

DASH与传统的SHS不同之处在于干涉仪一臂多了Δd的偏置量，这是由于风速引起的多普勒频移量非常小，仪器难以探测到。通过增加光程差偏置可以增大由风速引起的干涉相位改变，进而得到风速。然而，考虑到干涉调制度会随光程差的增加而减小，因此DASH存在一个最优光程差[6]

(2)

式(2)中，σD为高斯线型的线宽，σ0为谱线的中心波数，k为玻尔兹曼常数，T为大气的热力学温度，m为辐射源原子的质量，c为真空中的光速。

2 干涉数据处理方法

DASH结合了MI和SHS技术，但是数据处理算法又与二者完全不同。国外的相关文献[6]已经给出了空间外差相位计算的详细步骤，然而从其推导的干涉方程不难看出，其中并没有考虑加窗对干涉方程和相位计算的影响。事实上，窗函数对复原干涉图和相位差曲线有着不可忽视的作用，有必要对其进行深入分析。

2.1 干涉图预处理

DASH通过分析干涉相位的变化来解析风速，因此干涉条纹的质量直接决定了风速反演的精度。影响干涉条纹质量的主要因素有两个，一是在提取干涉图时，由于每个像元具有不同的响应，并且同时叠加了探测器噪声，导致记录的干涉图质量下降；二是在发生干涉时由于两臂通光的不一致性和光学系统未对准等原因致使条纹畸变[8]。

相应的预处理主要包括干涉图去噪声和平场校正。通过对干涉图进行平均和非均匀性校正[8]可以极大程度降低噪声，通过对干涉图进行平场校正[7]可以减小干涉相位的绝对误差。这在相关文献中都进行了详细分析，在此不再赘述。

2.2 复原干涉图

经预处理后的单频率干涉数据，傅里叶变换得到

f(σ)=F(C+CE(L)cos(2π(σ-σL)L))

(3)

其中E(L)为干涉调制函数，C为常数，f(σ)为干涉图的频谱，它由正频率的真实光谱以及负频率的对称谱组成。

在光谱域，加窗(T(σ))去除负频率成分(图2)。

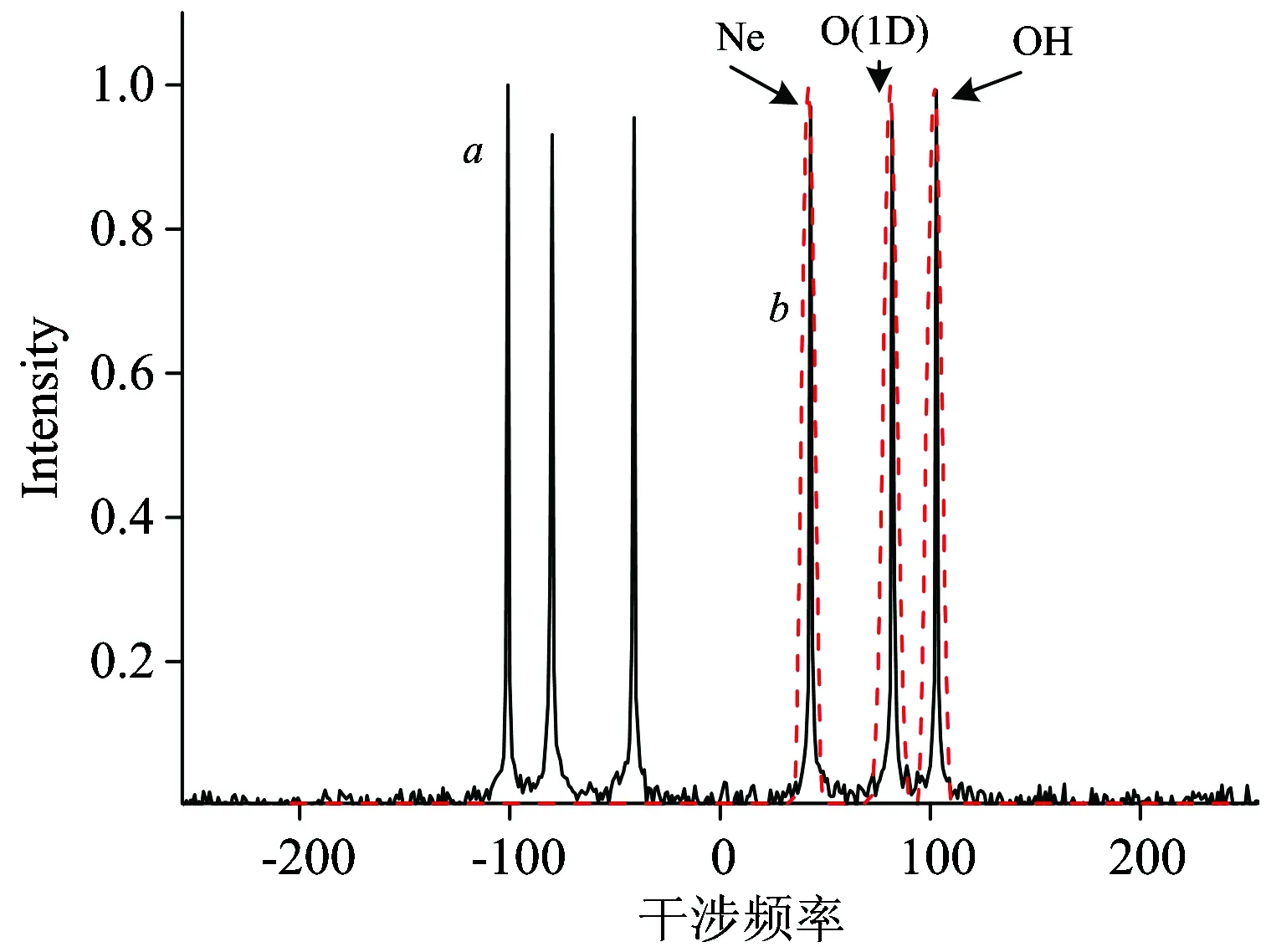
图2 曲线a模拟Ne校准灯和气辉发射光谱；曲线b隔离光谱的窗函数

Fig.2a: The spectrums of Ne calibration line and emission lines;b: window functions used to isolate individual emission lines

T(σ)f(σ)=T(σ)F(C)+

(4)

其中，T(σ)F(C)=0。傅里叶逆变换得到复干涉图I′(L)

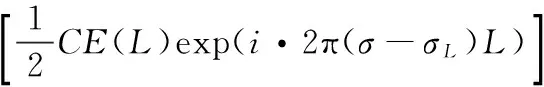
(5)

式中，C为常数，⊗为卷积运算。

2.3 求解干涉相位

通过干涉图的实虚部比可以得到干涉相位如下

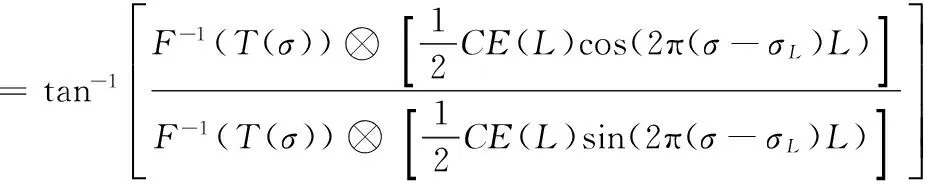
(6)

根据式(3)，理论的干涉相位为φ理论=2π(σ-σL)L。而实际相位计算方程中产生了不能相消的乘性因子F-1(T(σ))[式(6)]，因此由计算出的相位曲线产生极大的误差。

2.4 计算风速

通过上述处理步骤得到的式(7)为干涉图总相位，由基准相位和频移相位两部分组成[式(7)]

φ总=φ基准+φw

(7)

式中，φ基准表示零风速下的基准相位，它是干涉图的固有相位。而φw表示频移相位，实际为零风速和某一确定风速的相位差[7]

(8)

其中，σ为零风速的波数，v为多普勒风速，c为真空中的光速。由式(8)能够计算得到风速的大小。

3 仿真分析

以630.03 nm的氧红线气辉为例，它存在于200～300 km的热电离层区域，典型温度为1 000 K[1]，风速范围在0～100 m·s-1。根据谱线热展宽计算DASH干涉仪的最优光程差为Lopt=4.2 cm，有效光程差范围为2.44～5.90 cm。

3.1 复原干涉图误差及讨论

对于有一定温度展宽的高斯型气辉谱线，其干涉图的包络随着光程差的增加而逐渐减小。图3取三种典型的窗函数类型说明其对复原干涉图的影响。

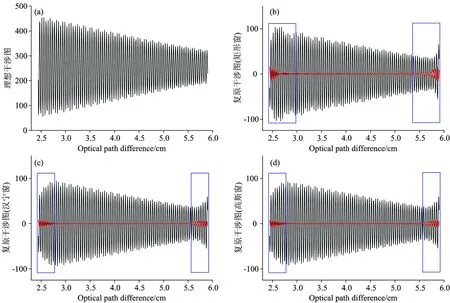
图3 模拟干涉图

(a)：Ideal interferogram; (b), (c), (d)：Black curves corresponding to the real part of the isolated interferogram under Rectangle window, Hanning window and Gauss window, respectively; red curves corresponding to three window spectra, respectively

图3(a)说明理想干涉图的包络随着光程差的增加均匀变化。对比图3(b)—(d)看出，卷积汉宁窗和高斯窗的复原干涉图，其包络两端变形区域较窄；而卷积矩形窗后的干涉图，包络变形区域增大。这是由于矩形窗频谱具有较大的旁瓣(红色线)，而其他两种窗型的频谱旁瓣几乎为零，对干涉图包络的影响较小。

由于对干涉相位的计算是通过复原干涉图实虚部比得到，因此干涉图的误差直接导致计算的干涉相位不准确，进而影响了风速反演精度。

3.2 相位差误差、风速误差及讨论

3.2.1 窗函数因子对相位差误差的影响

(1)窗函数类型

为了说明不同类型的窗函数对结果的影响不同，图4给出由复原干涉图计算的相位差和风速误差曲线，分别对应矩形窗、三角窗、汉宁窗、汉明窗和高斯窗，设频移风速为100 m·s-1。

由图4(a)，相位差随着光程差的增加而增大，但是在低光程差区域，模拟相位差比理论相位差偏大，约等同25 m·s-1的风速计算误差；高光程差区域，模拟相位差比理论相位差偏小，约等同-48 m·s-1的风速误差；中间区域相位随光程差变化仍然保持较好的线性关系，造成的风速误差低于1 m·s-1。

图4 不同窗函数的相位差(a)和风速误差(b)

从相位曲线上较难分辨出不同窗函数的影响，因此右图截取了3.2～5.1 cm光程差范围内的风速误差曲线。从曲线线型来看，矩形窗(黑色)和汉明窗(粉色)由于频谱泄漏使风速误差随着光程差变化出现了规律的震荡，其他三种窗函数下的风速误差变化相对平稳。从曲线误差上看，汉宁窗(蓝色)和汉明窗(粉色)的风速误差最小，低于0.3 m·s-1，高斯窗(绿色)次之，矩形窗(黑色)最大，约0.8 m·s-1。

虽然每个光程差点都能反演风速，但是兼顾相位和干涉调制度的考虑，用最优光程差点计算出的风速误差如表1。

表1的结果与图4一致，仿真证明，用汉宁窗能够在频谱泄漏相对较少的条件下对相位误差的贡献最小。

(2)窗长度

对汉宁窗给定不同的半高宽，得到图5(假设模拟的风速为100 m·s-1)干涉相位差曲线。

表1 窗函数类型与风速误差的关系

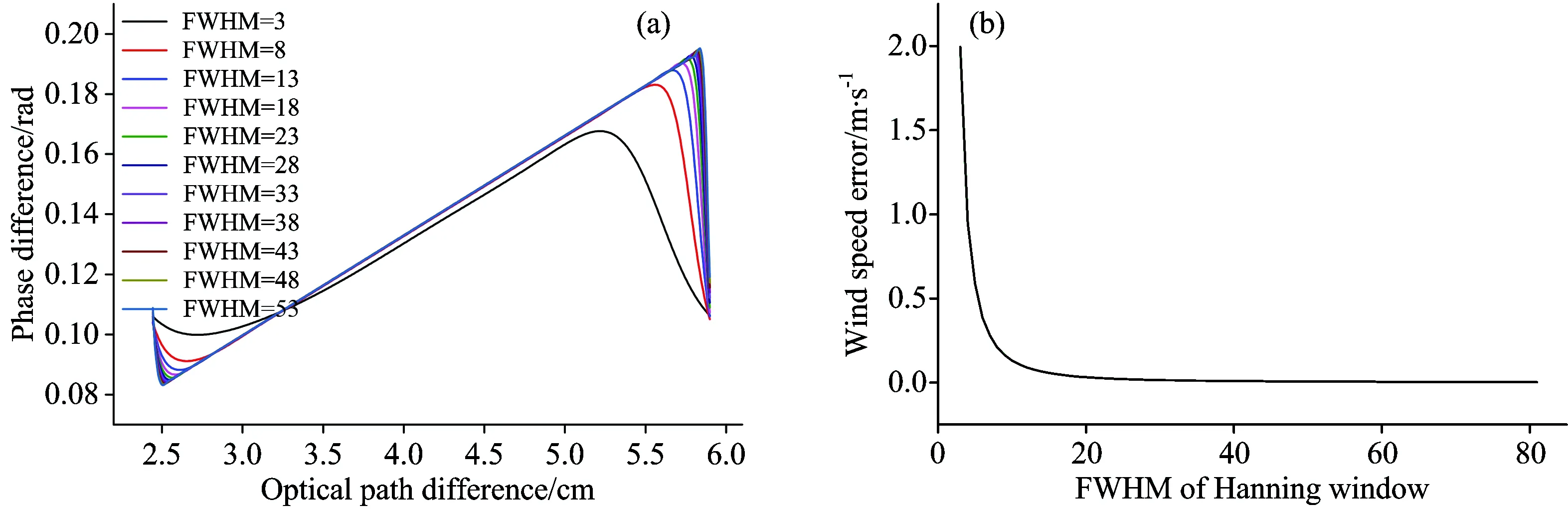
图5 (a)不同半高宽汉宁窗的相位差；(b)风速误差与汉宁窗半高宽的关系曲线

图5是汉宁窗半高宽与风速误差的关系。由图5(a)，随着窗长度的增加，由窗函数频谱引起的相位差两端畸变的区域变小；由图5(b)，随着窗长度的增加，风速反演误差降低。图5说明，在理想情况下，窗函数的宽度越宽，对相位和风速的影响越小。

3.2.2 噪声和平场因子对相位差误差的影响

对干涉图添加噪声和抛物线型的平场因子，计算给出图6的相位关系。

图6(a)是对理想干涉图进行傅里叶变换和逆变换后得到的干涉相位差关系；图6(b)是对干涉图添加了1%的噪声和抛物线因子后计算得到的干涉相位差关系。对比两个图可以看出，噪声和平场因子的加入对相位的影响非常显著，使原本平滑变化的相位差曲面产生起伏不定的抖动，这一变化直接导致了风速反演的精度。

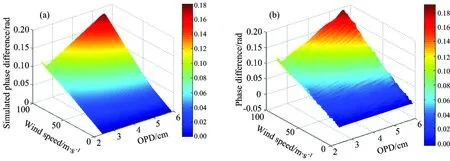
图6 风速0～100 m·s-1变化时相位差与光程差的关系

对干涉图添加的误差2%～0.4%变化对应的理论风速误差范围如表2。

表2 噪声与风速误差关系

由表2可以看出，当添加2%的噪声时，绝对风速误差约5 m·s-1；随着噪声减小到只有0.4%时，绝对风速误差约低于2 m·s-1。为了控制一定的风速反演精度，通过对探测器制冷等方式减小噪声，进而可以降低风速误差。

实际情况下，噪声和平场因子的变化更加复杂，因而带来的风速误差更大，仿真结果一方面说明了干涉图预处理的必要性，另一方面也对系统风速精度的确定提供参考。

4 结 论

非对称空间外差光谱技术是被动式风场探测的新方向，但是有别于传统的“四强度法”，通过傅里叶变换求解相位，进而得到风速。在这个过程中，不仅系统的噪声使干涉图产生误差，而且窗函数因子的不确定性使处理后的复原干涉图发生畸变。这就要求在数据处理时需要考虑两个方面，一是对干涉图进行预处理，二是选择合适的窗函数对光谱加窗。从窗函数和噪声对干涉相位的影响进行仿真得出以下结论：

由于卷积了窗函数的频谱，导致复原干涉图包络较之理想干涉图在低光程差和高光程差区域发生明显的变形，直接影响了干涉相位的计算。通过选择中心区域的光程差点可以较准确地反演出风速，因而不需要对相位曲线进行校正。

对比不同窗函数下的风速误差得出：矩形窗频谱的震荡导致其对应的风速误差曲线产生波动[图4(b)]，采用汉宁窗则使风速曲线的波动最小，误差也较低，此种情况更接近于理论的相位曲线，因此最终选择汉宁窗作为谱隔离函数。

模拟窗长度与干涉相位差的关系说明，随着窗长度的增加，风速误差快速衰减并趋近于零。但是实际探测时，波段内往往有多条目标线、干扰线以及校准线，受到相邻谱线的影响，窗长度不可能很大。因此，通过合理选择窗函数类型和窗长度，能够使风速误差限制在0.5 m·s-1范围内。

在此基础上给出了系统噪声与相位差和风速误差的关系：随着噪声的增加，风速误差增大。这说明为了获取高精度的风速，一方面需要控制系统噪声使之降至最低，另一方面要对采样的干涉图进行预处理进一步减小噪声的影响。

[1] Shepherd G G, Thuillier G, Gault W A, et al.Journal of Geophysical Research: Atmospheres (1984—2012), 1993, 98(D6): 10725.

[2] Englert C R, Harlander J M, Emmert J T, et al.Optics Express, 2010, 18(26): 27416.

[3] Solheim B, Brown S, Sioris C, et al.Atmosphere-Ocean, 2013，53(1): 1.

[4] Englert C R, Harlander J M, Brown C M, et al.MIGHTI: The Spatial Heterodyne Instrument for Thermospheric Wind Measurements on Board the ICON Mission，in Fourier Transform Spectroscopy and Hyperspectral Imaging and Sounding of the Environment.Optical Society of America, 2015: FM4A.1.

[5] Englert C R, Harlander J M, Babcock D D, et al.Proc.SPIE, 2006, 6303: 63030T.

[6] Englert C R, Babcock D D, Harlander J M.Applied Optics, 2007, 46(29): 7297.

[7] Marr K D, Englert C R, Harlander J M.Optics Express, 2012, 20(9): 9535.

[8] LI Zhi-wei, XIONG Wei, SHI Hai-liang, et al(李志伟，熊 伟，施海亮，等).Acta Optica Sinica(光学学报), 2014, 34(5): 0530001.

(Received May 11, 2015; accepted Sep.28, 2015)

*Corresponding author

Data Processing Method of Asymmetric Spatial Heterodyne Interferogram for Wind Measurement

SHEN Jing1, 2, 3，XIONG Wei1, 2, 3*，SHI Hai-liang1, 3，LI Zhi-wei1, 3，HU Guang-xiao1, 3，QIAO Yan-li1, 3

1.Anhui Institute of Optics and Fine Mechanics，Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei 230031, China 2.University of Science and Technology of China, Hefei 230026, China 3.Key Laboratory of Optical Calibration and Characterization of Chinese Academy of Sciences, Hefei 230031, China

By using doppler asymmetric spatial heterodyne spectroscopy and doppler effect, the wind speed can be achieved through detecting the interferogram of airglow in the upper atmosphere.This paper mainly analyses the data processing method of the interferogram and then derive the interferometer phase in order to get the wind speed.Comparing with the traditional spatial heterodyne spectroscopy, not only the noise and error of the system should be taken into consideration, but the window function that used to isolate the spectrum has a great influence during the data processing.Then the effect of window type and window width on phase difference of interferogram and the wind error curve are simulated through software.On basis of this the wind error curve under the noise of system and flat field factor are simulated by choosing appropriate window function.The window function simulation indicates that although the joining of window leads to a distortion of the interferogam and phase, the wind speed error can be less than 0.5% with Hanning window in the appropriate optical path difference.The noise of the system simulation indicates that the wind speed error increases with the noise, so it is necessary to control the system noise and preprocess the sampling data.The research on data processing method has great theoretical significance and practical value for designing the system parameter and improving the precision of spatial heterodyne wind detection.

Wind measurement; Asymmetric spatial heterodyne spectrometer; Interferogram; Fourier transform; Window function; Noise

2015-05-11，

2015-09-28

中国科学院创新基金项目(CXJJ-14-S91)资助

沈 静，1988年生，中国科学技术大学博士研究生 e-mail: xingyang_jing@163.com *通讯联系人 e-mail: frank@aiofm.ac.cn

O433.4

A

10.3964/j.issn.1000-0593(2016)09-3014-06