基于Gabor变换的TDLAS检测信号的降噪研究
崔海滨,杨 柯, 2,张 龙,吴晓松,刘 勇,王 安,李 慧,计 敏*
1.中国科学院合肥物质科学研究院应用技术研究所,安徽 合肥 230031 2.中国科学技术大学,安徽 合肥 230026 3.北京市烟草质量监督检测站,北京 100029
基于Gabor变换的TDLAS检测信号的降噪研究
崔海滨1,杨 柯1, 2,张 龙1,吴晓松1,刘 勇1,王 安1,李 慧3,计 敏1*
1.中国科学院合肥物质科学研究院应用技术研究所,安徽 合肥 230031 2.中国科学技术大学,安徽 合肥 230026 3.北京市烟草质量监督检测站,北京 100029
可调谐二极管激光吸收光谱(TDLAS)技术结合波长调制光谱(WMS)技术是用于痕量气体检测的重要技术手段。通过锁相放大器进行谐波检测,对解调得到的二次谐波信号进行分析可获得气体吸收的信息。但由于二次谐波信号受到噪声的影响,降低了检测系统的精度和稳定性。为了提高TDLAS检测系统的信噪比(SNR),提出了一种基于Gabor变换对二次谐波信号进行数字滤波降噪的方法。以CH4在1 653.72 nm处的吸收光谱为例,通过仿真和实验对该降噪方法的有效性进行了验证。仿真结果表明,通过Gabor变换对信噪比为0dB的二次谐波信号进行处理后,系统的信噪比可提高15.73 dB。实验结果表明,基于Gabor变换进行降噪处理后,CH4浓度在0.001%~0.02%区间内与二次谐波峰值的线性相关系数r达到了0.996 59,且系统的检测精度和稳定性明显提高。
TDLAS;Gabor变换;二次谐波;降噪
引 言
TDLAS技术因具有高灵敏度、高选择性、响应快以及能够实现在线检测等优点而广泛应用于痕量气体检测。对于痕量气体在近红外波段的吸收进行检测,WMS和直接吸收光谱技术是TDLAS常用的两种技术手段。相对直接吸收光谱技术,WMS通过将检测频率移到高频区可以抑制检测频带以外的噪声尤其是低频噪声的影响,从而提高检测精度和系统信噪比[1]。但是,基于WMS并利用锁相放大器得到的二次谐波信号受到光学干涉条纹噪声、探测器噪声等噪声干扰,使得每次扫描得到的信号不完全相同[1-2],这也降低了检测系统的精度和稳定性。因此,如何提高TDLAS检测系统的信噪比具有重要的研究意义。
为了提高TDLAS检测系统的信噪比,通常采用扣除背景的方法来减小由于标准具效应所引入的光学干涉条纹噪声的影响,然后对扣除背景的采集信号进行累加平均使谱线信号平滑。为进一步降低各种噪声的影响,采用数字滤波和数字信号处理技术可以进一步提高系统的信噪比和检测灵敏度,很多研究者也针对此提出了不同的算法。Leleux[3]和阚瑞峰[4]等分别采用Kalman滤波法和α-β-γ滤波法对反演得到的浓度数据进行进行滤波,但没有对二次谐波信号进行滤波处理。张志荣[5]等采用非线性最小二乘法拟合二次谐波信号,但这种方法需要精确锁定待测气体的吸收谱线位置,保证标准信号谱线和测量信号谱线的中心重合。最近,Li[6-7]等将离散小波变换应用于光谱降噪,取得了较好的结果。但对于小波变换,如Li[6]指出,小波类型、阈值的选取方法以及分解尺度等参数的选取都对结果有重要影响。
Gabor变换作为一种线性联合时频分析方法,一直以来都是研究非平稳信号的常用方法。通过Gabor变换可以得到一系列的Gabor展开系数,而Gabor展开是Gabor在1946年提出[8],它能够反映信号频率成分随时间的变化特性。通过Gabor展开将信号表示成一系列的经过时移和频率调制的高斯窗函数线性加权之和,其权值大小对应各分量的Gabor系数幅值。通过阈值法对Gabor变换得到的Gabor系数进行修正,即修正噪声分量对应的Gabor系数,然后利用修正得到的Gabor系数进行Gabor展开即可实现降噪功能。Gabor变换已经成功应用在多普勒超声谱降噪[9]、语音降噪[10]等领域。经过降噪处理后的信号信噪比不但明显提高,而且对于信号的特征并没有明显改变。本文通过Gabor变换对TDLAS检测系统的二次谐波信号进行降噪处理,研究了这种方法对信号信噪比以及检测系统精度和稳定性的影响。
1 Gabor变换降噪原理
1.1 Gabor变换
对于周期为L的数字信号s[k],其离散Gabor展开
(1)
其中ΔM和ΔN分别指时间和频率采样间隔,h(k)为综合窗函数,M和N表示时域和频域的采样点数,且有
ΔMM=ΔNN=L
(2)
对于Gabor系数,可以表示为
(3)
其中γ*[k]与γ[k]为互为共轭,γ[k]为h(k)的对偶分析窗函数。时—频域总共的采样点数MN和信号的周期L的比值被称为过采样率,用a表示
a=MN/L
(4)
其中,a<1时被称为欠采样;a=1时被称为临界采样;a>1时被称为过采样。为了能够保证能够很好的进行信号重构,要求a≥1。
1.2 降噪原理
降噪算法的原理图见图1。
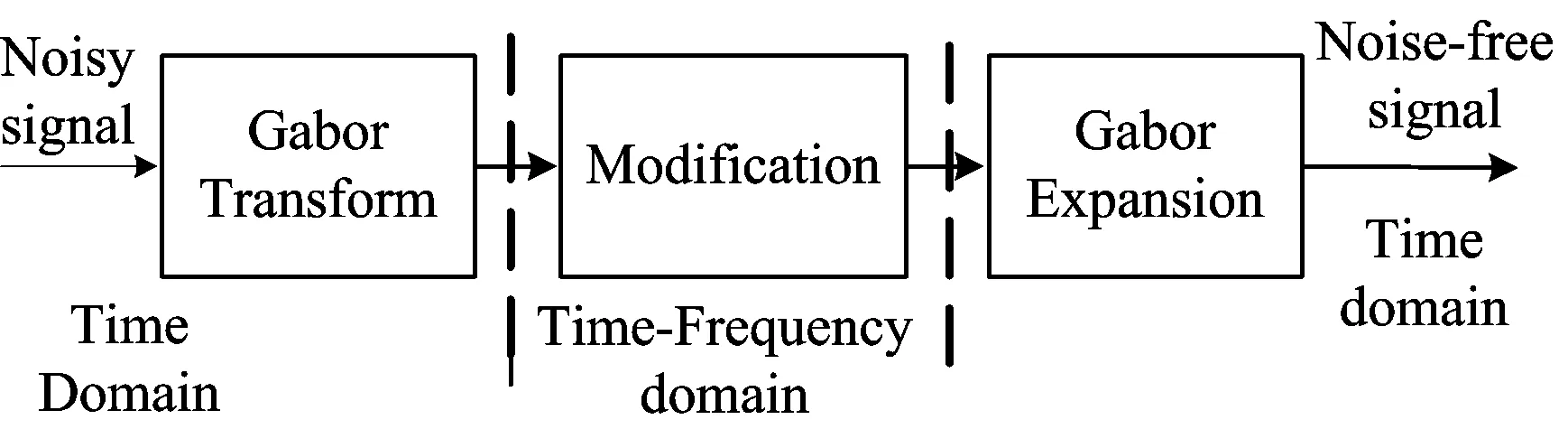
图1 Gabor变换降噪原理图
假设含有噪声的信号x[k]由信号s[k]和噪声e[k]两部分组成
x[k]=s[k]+e[k]
(5)
降噪的目的是从x[k]中提取s[k],实现步骤如下:
(1)对含有噪声的信号x[k]进行离散Gabor变换,计算对应的Gabor系数。因为Gabor变换是一种线性变换,所以对式(5)进行变换可得
cx[m,n]=cs[m,n]+ce[m,n]
(6)
其中cx[m,n],cs[m,n]和ce[m,n]分别代表了x[k],s[k]和e[k]进行离散Gabor变换所得到的Gabor系数。
(2)Gabor系数幅值的大小可以用于反映信号功率的大小。信号s[k]相对噪声e[k]的功率较大且两者对应各自的Gabor系数在时-频面上分布不同[11]。对于信号s[k],其对应的Gabor系数cs[m,n]在时—频面上分布比较集中,幅值较大。噪声e[k]对应的Gabor系数ce[m,n]分布在整个时—频面上,幅值较小。通过选取合适的阈值对幅值较小的Gabor系数进行修正,即对其置零,则可以减小噪声所带来的影响。具体修正算法如下
cx[m,n]=cx[m,n]cx[m,n]≥threshold(cmax-cmin)
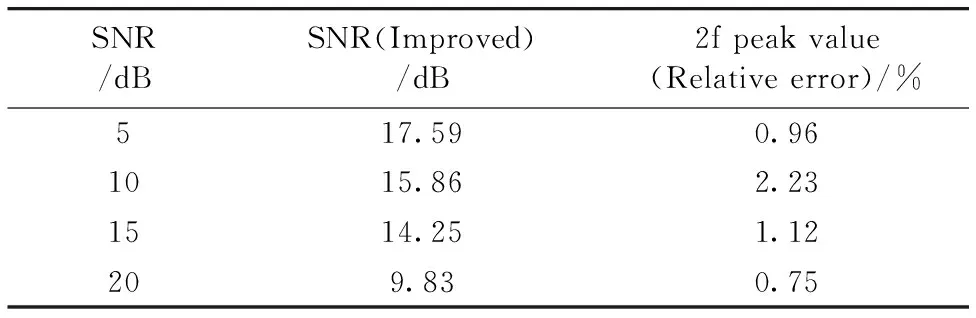
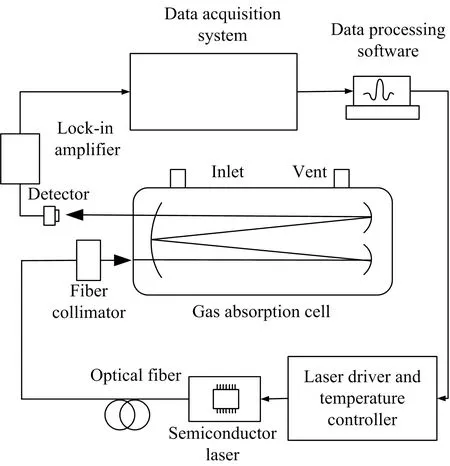
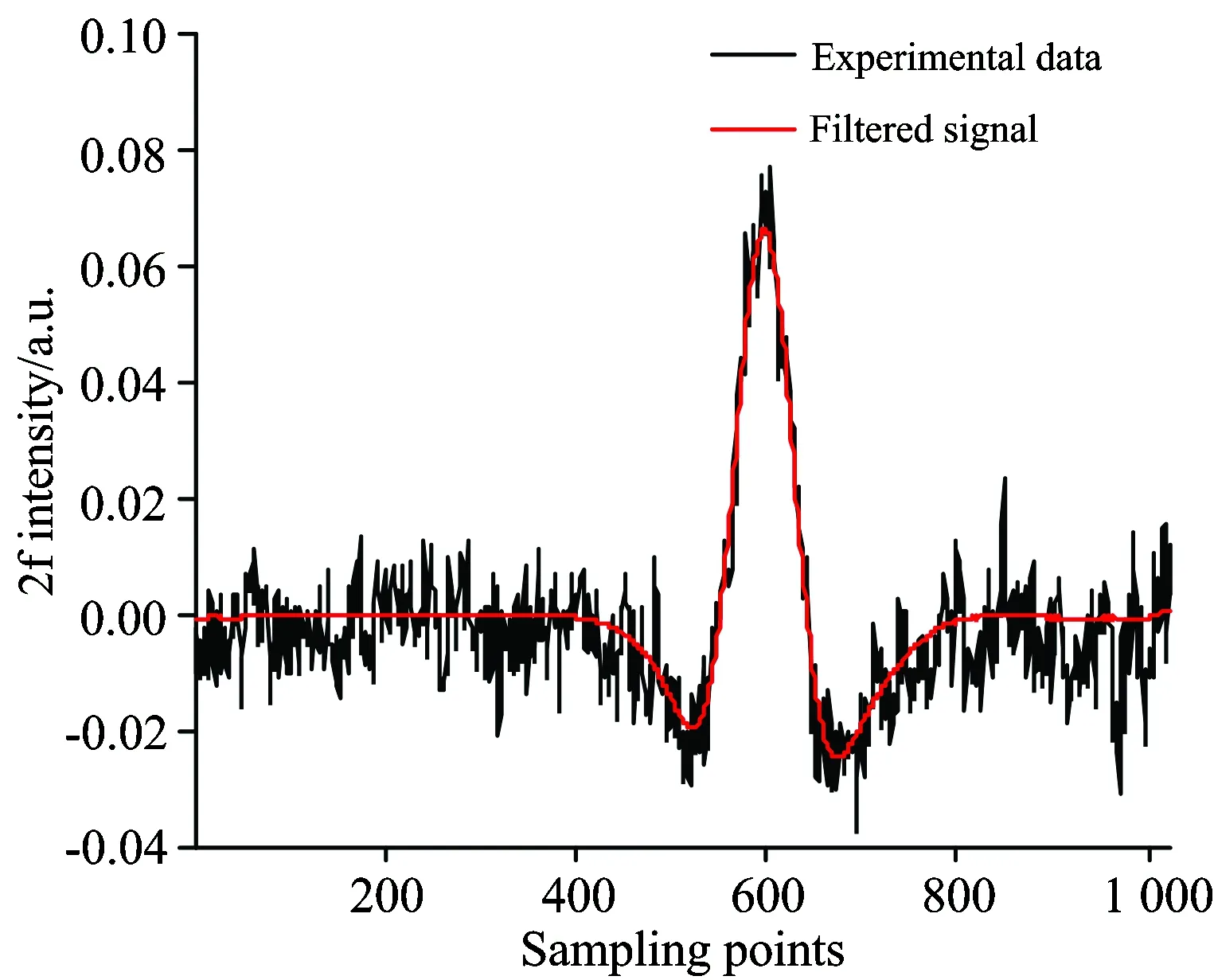
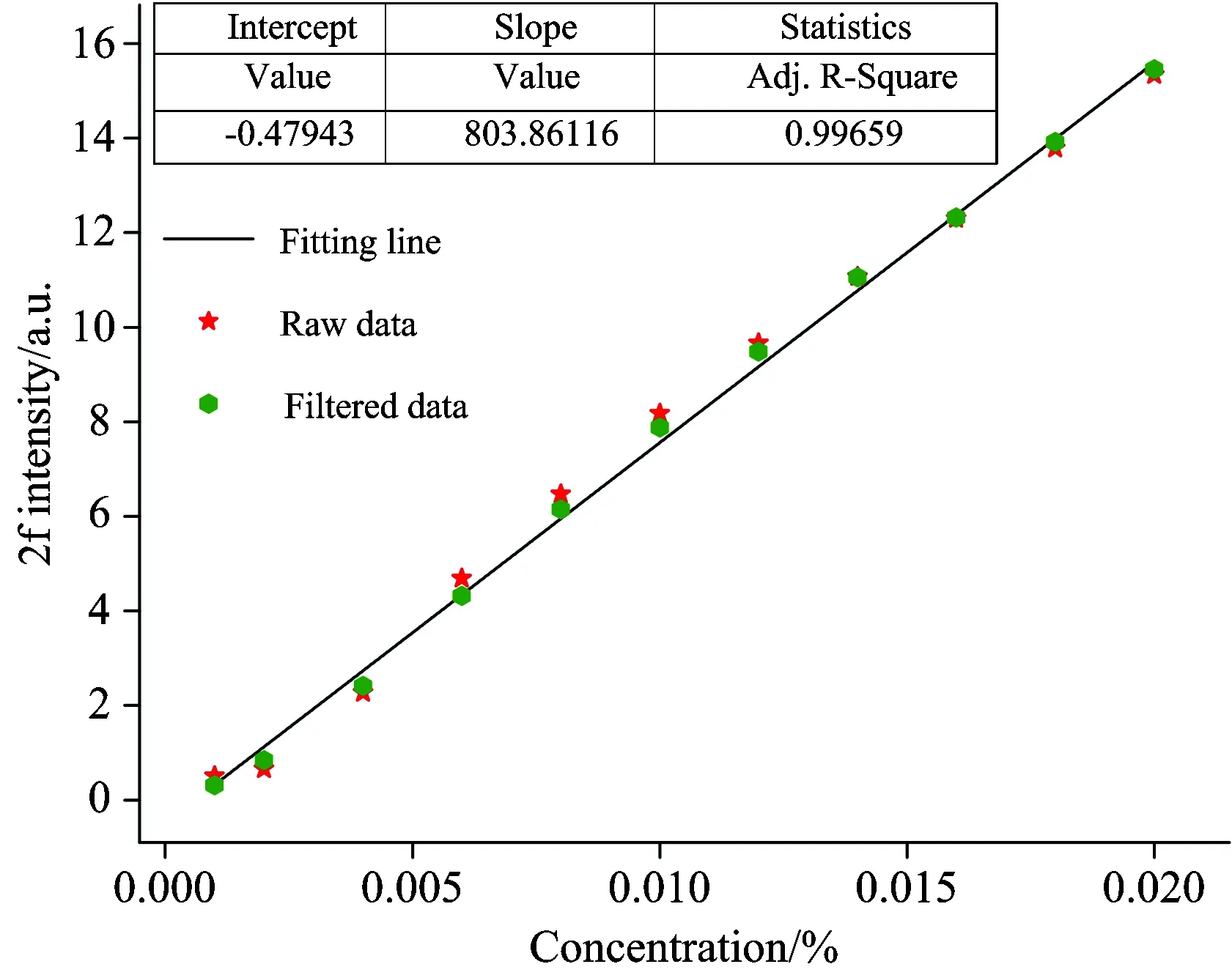
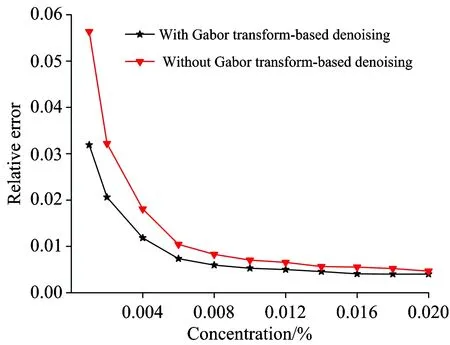
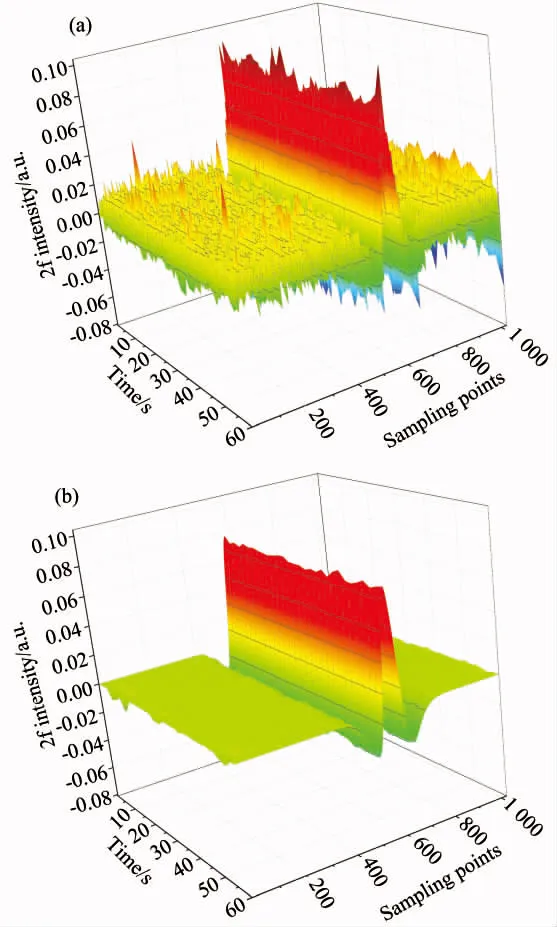
cx[m,n]=0cx[m,n] cmax和cmin分别是指Gabor系数幅值中的最大值和最小值。 (3)根据(2)所得到的Gabor系数,进行Gabor展开,重构信号,从而将信号s[k]从x[k]中提取出来。 为了验证Gabor变换用于降噪的方法在二次谐波信号降噪中应用的有效性,以CH4在1 653.72 nm附近2ν3带R(3)支的吸收谱线为例进行仿真分析。通过MATLAB仿真得到二次谐波信号并加入高斯白噪声,在不同的信噪比下,进行降噪处理。为了对比降噪效果,选取信噪比这一指标进行分析。信噪比定义如下 (7) 通过查询HITRAN 2008[12]数据库可知,CH4在近红外(1 653.72±0.01) nm波长范围内存在3条吸收谱线。可以近似将这3条吸收谱线看作一条吸收谱线,其吸收谱线线强大小为这3条吸收谱线线强之和。在一个大气压条件下,谱线展宽以洛伦兹展宽为主,归一化的洛伦兹线型表达式为 (8) (9) 取m=2.2,通过MATLAB仿真得到的二次谐波信号如图2所示。 图2 二次谐波吸收信号 通过MATLAB的AWGN函数加入高斯白噪声。当信噪比SNR=0 dB时,在仿真信号中取1 024个采样点,设其采样率大小为50 kHz。对采样得到的信号进行离散Gabor变换前,首先要对高斯窗的相关参数进行设置。为了保证过采样率a≥1,选取时—频域的采样点数M和N的大小分别为1 024和512,高斯窗宽度为1 024。 为了能够有效的降噪,选取合适的阈值是关键。阈值的选取与噪声密切相关,在0~1的范围内以信噪比SNR为指标进行测试。当阈值选取为0.65时,经过降噪处理得到的信号信噪比SNR取得最大值。因此选取0.65作为阈值进行降噪。得到的Gabor谱图如图3所示,图中Gabor系数幅值的大小反映了信号功率的大小。 图3 (a)含噪信号;(b)含噪信号Gabor谱图;(c)过滤后信号;(d)过滤后信号Gabor谱图 通过计算降噪前后的二次谐波信号可知:信噪比提高了15.73 dB,且滤波后的二次谐波信号与通过仿真得到的二次谐波信号基本重合。分布在整个时—频面上噪声信号经过降噪处理后得到有效的抑制。为了进一步对这种方法的降噪效果进行验证,滤波参数不变,选取信噪比SNR分别为5,10,15和20 dB这四种情况下含噪的二次谐波信号进行仿真测试,结果如表1所示。 表1 基于Gabor变换的降噪测试 由表1分析可知,经过降噪处理后,系统信噪比提高了近15 dB,而且二次谐波峰值相对误差小于3%。说明针对高斯白噪声,通过离散Gabor变换能够有效提高系统信噪比而且对目标信号特征(二次谐波峰值)影响较小。需要指出的是,仿真信号中加入的噪声是最常见的高斯白噪声,与实际的检测系统噪声类型并非完全相同。因此,接下来针对实际检测系统采集得到的二次谐波信号进行降噪分析,以探究该算法的实际应用效果。 3.1 装置 TDLAS检测系统由激光器驱动和温度控制系统、可调谐二极管半导体激光器、气体吸收池、锁相放大器、数据采集系统、计算机等组成。激光器驱动和温度控制系统向激光器提供50 Hz的锯齿波扫描信号和40 kHz的正弦波调制信号,激光器输出波长在CH4中心吸收波长(1 653.72 nm)附近扫描。激光通过气体吸收池,经多次吸收反射后到达光电探测器上。经过锁相放大器进行放大处理和二倍频谐波解调得到二次谐波吸收信号。最后通过数据处理软件对数据采集系统采集到的数据进行处理,得到用于浓度反演的二次谐波峰值。 图4 用于CH4检测的TDLAS装置图 3.2 检测系统标定 首先用高纯氮气冲洗气体吸收池,待光谱稳定后记录此时的“零气”光谱作为CH4吸收光谱的背景光谱。其中数据采集系统的采样率、每次扫描的采样点数以及高斯窗参数的设置与仿真实验相同。以降噪后信号信噪比为指标,选取不同阈值进行测试。经过测试,阈值的大小选定为0.75。然后将一定浓度的CH4气体通入气体吸收池,通过软件对扣除背景后的二次谐波信号进行降噪处理。当通入的CH4浓度为0.001%时,得到的二次谐波如图5所示。 图5 实验数据和过滤后数据 从图5可以看出,经过Gabor变换对二次谐波进行降噪处理,不但可以有效抑制噪声的干扰而且可以对基线进行校正。对于实验得到的二次谐波数据,在计算信噪比SNR时, 由于无法得到理想的二次谐波吸收数据,因此选择二次谐波信号的峰值与吸收峰周围的噪声幅值标准差来计算。通过计算,基于Gabor变换进行降噪处理后,系统的信噪比由22.26 dB提高到52.25 dB。与理论的二次谐波信号形状不同,实验得到的二次谐波信号并非关于中心波长偶对称的。这主要是由于受到其他奇次谐波成分的叠加以及剩余幅度调制等因素的影响。 为了进一步测试算法的降噪效果,在0.002%~0.02%区间,利用气体质量流量计配置了10个梯度浓度的CH4气体进行测试。然后计算得到的二次谐波信号峰值与气体浓度之间的线性相关系数,分析两者之间的相关性。 图6是依据不同浓度CH4标气与其二次谐波峰值得到的标准曲线,可以看出二次谐波峰值与对应的气体浓度之间具有很好的线性关系,因此可以利用该标准曲线计算被测CH4浓度。 图6 二次谐波信号强度与气体浓度之间的线性关系 3.3 检测系统精度 为确定检测系统的精度,在使用Gabor变换进行降噪和未进行降噪处理两种情况下,利用拟合得到的曲线对不同样品的浓度进行测量。用浓度测量值与真实值进行对比,计算得到相对误差曲线,如图7所示。从图7可知,经过降噪处理和未经过处理这两种情况下得到的气体浓度相对误差值随着被测气体浓度增大而减小,且前者小于后者。这是由于当样品浓度较低时,得到的二次谐波信号由于受噪声干扰严重,其信噪比较低,从而导致了测量得到的气体浓度相对误差较大。而随着被测气体浓度逐渐增大时,二次谐波信号的峰值以及信号的信噪比也随之逐渐增大。噪声的影响相对减小,从而使得在降噪处理和未降噪处理这两种情况下得到的气体浓度相对误差值之间的差距逐渐缩小。因此,当被测气体浓度较低时,通过Gabor变换进行降噪处理不但可以提高检测信号信噪比并且在一定程度上提高系统检测精度。 图7 检测误差 图8 60 s检测得到的二次谐波信号 3.4 检测系统稳定性 在实验检测中,尤其是在低浓度检测的情况下,噪声的干扰会使得检测得到的二次谐波信号不够稳定。在本次实验中,选择浓度为0.001%的样品气体进行测试。测量持续60 s,每隔2 s记录一次数据。通过对比降噪前后的二次谐波信号以及反演得到的气体浓度值和标准差来反映检测系统的稳定性。实验得到的二次谐波信号如图8所示,计算结果见表2。由实验结果可知,通过Gabor变换对二次谐波信号进行降噪处理后,信号的信噪比明显提高,计算得到的气体浓度值更接近真实值且相对稳定。 表2 检测结果 数字滤波和数字信号处理已经在TDLAS检测系统中取得了广泛的应用。相对模拟滤波的方法,数字滤波的方法对系统硬件资源要求更低但应用更加灵活。本文将Gabor变换应用于TDLAS检测系统中二次谐波信号的降噪处理。以CH4在1 653.72 nm处的吸收光谱为例,通过仿真和实验对这种方法的降噪效果进行了验证,并对降噪后的二次谐波峰值与气体浓度之间的线性关系以及检测系统的精度和稳定性进行了分析。结果表明这种方法不但能够有效提高检测系统的信噪比,而且能够用于提高系统检测精度和稳定性。这种降噪方法也有望推广到其他的光谱学降噪领域。 基于Gabor变换进行降噪成功的关键是Gabor系数阈值的选取。为了取得较好的降噪效果,需要根据实际噪声大小,进行阈值调节。因此如何根据实际噪声大小自动调节阈值进行自适应降噪是接下来继续开展的工作。 [1] Li J, Yu B, Zhao W, et al.Applied Spectroscopy Reviews, 2014, 49(8): 666. [2] Hodgkinson J, Tatam R P.Measurement Science and Technology, 2013, 24(1): 012004. [3] Leleux D P, Claps R, Chen W, et al.Applied Physics B, 2002, 74(1): 85. [4] Kan Ruifeng, Liu Wenqing, Zhang Yujun, et al.Chinese Physics, 2006, 15(6): 1379. [5] ZHANG Zhi-rong, DONG Feng-zhong, TU Guo-jie, et al(张志荣, 董凤忠, 涂郭结, 等).Journal of Optoelectronics·Laser(光电子·激光), 2010, 21(11): 1672. [6] Li J, Parchatka U, Fischer H.Applied Physics B, 2012, 108(4): 951. [7] Tian G, Li J.Optica Applicata, 2013, 43(4): 803. [8] Gabor D.Journal of the Institution of Electrical Engineers-Part Ⅲ: Radio and Communication Engineering, 1946, 93(26): 429. [9] Zhang Y, Zhang H.IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2005, 52(10): 1861. [10] Erçelebi E.Applied Acoustics, 2004, 65(8): 739. [11] Lu Y, Joshi S, Morris J M.IEEE Transactions on Biomedical Engineering, 1997, 44(6): 512. [12] Rothman L S, Gordon I E, Barbe A, et al.Journal of Quantitative Spectroscopy and Radiative Transfer, 2009, 110(9): 533. [13] De Rosa M, Ciucci A, Pelliccia D, et al.Optics Communications, 1998, 147(1): 55. (Received Apr.22, 2015; accepted Aug.17, 2015) *Corresponding author Tunable Diode Laser Absorption Spectroscopy (TDLAS) Detection Signal Denoising Based on Gabor Transform CUI Hai-bin1, YANG Ke1, 2, ZHANG Long1, WU Xiao-song1, LIU Yong1, WANG An1, LI Hui3, JI Min1* 1.Institute of Applied Technology, Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei 230031, China 2.University of Science and Technology of China, Hefei 230026, China 3.Beijing Tobacco Quality Supervision & Test Station, Beijing 100029, China Tunable diode laser absorption spectroscopy (TDLAS) technology combined with wavelength modulation spectroscopy (WMS) technology is an important technique for trace gas detection.Detected with the lock-in amplifier, the second harmonic signal obtained after demodulation is analyzed to get the gas absorption information.However, the second harmonic signal is affected by noise which reduces the accuracy and stability of the detection system.To improve the signal to noise ratio (SNR) of the TDLAS detection system, a denoising method based on Gabor transform is proposed for second harmonic signal noise reduction.Taking the CH4absorption spectrum at 1 653.72 nm as an example, the effectiveness of the noise reduction method is verified through simulation and experiments.The simulation results show that the signal to noise ratio for the second harmonic signal of 0 dB can be improved 15.73 dB with Gabor transform-based denoising method.Experimental results show that with the Gabor transform-based denoising method, the linear correlation coefficientrcan be as high as 0.996 59 between the second harmonic peak value and the CH4concentration in the range of 0.001%~0.02%.At the same time, the detection accuracy and stability of the system have been improved significantly. TDLAS; Gabor transform; Second harmonic; Denoising 2015-04-22, 2015-08-17 国家自然科学基金项目(21203203)资助 崔海滨,1991年生,中国科学院合肥物质科学研究院应用技术研究所硕士研究生 e-mail:cuihaibin100@yeah.net *通讯联系人 e-mail:jimin@aiofm.ac.cn TH744.1 A 10.3964/j.issn.1000-0593(2016)09-2997-062 仿真与分析
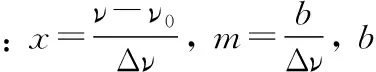
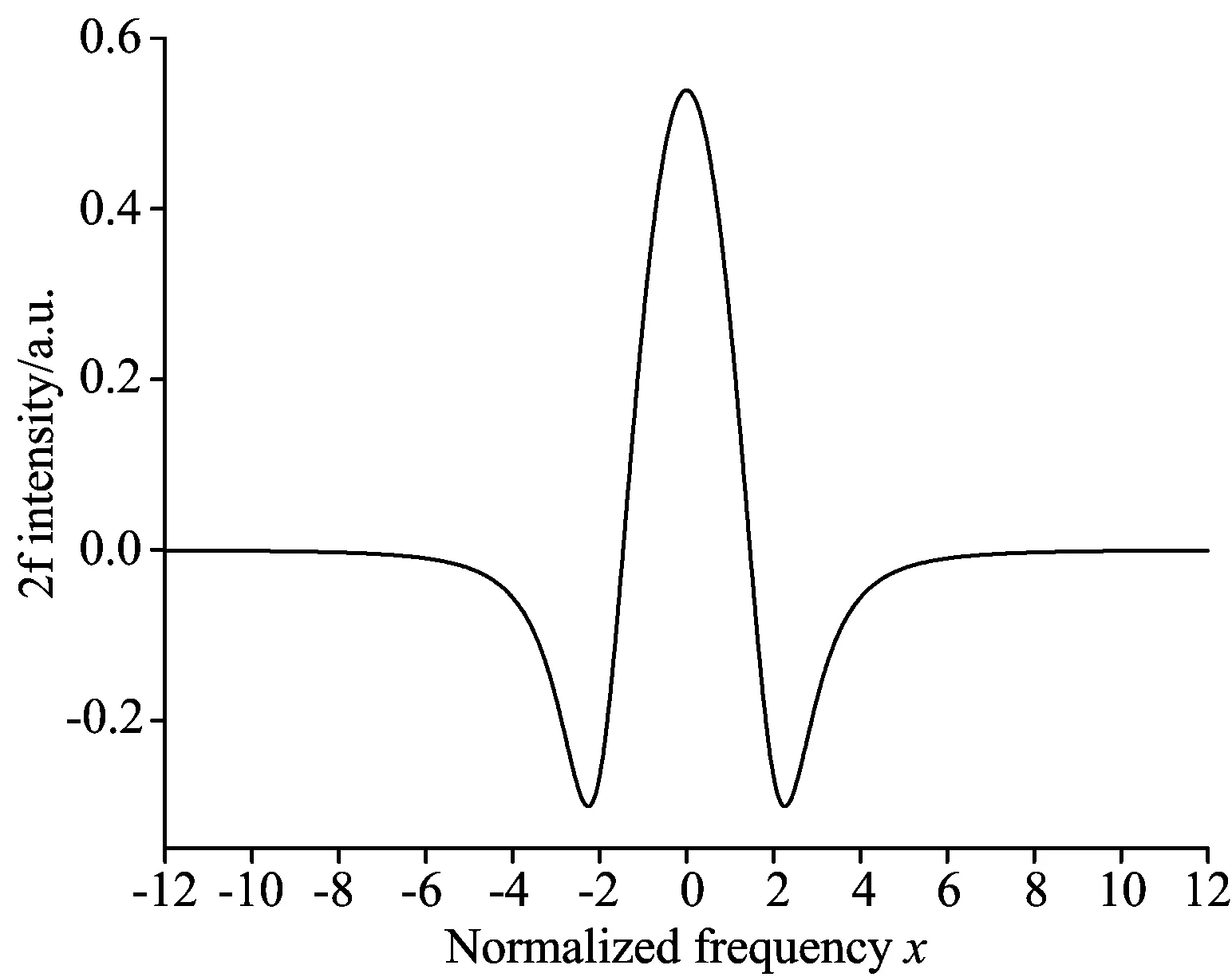
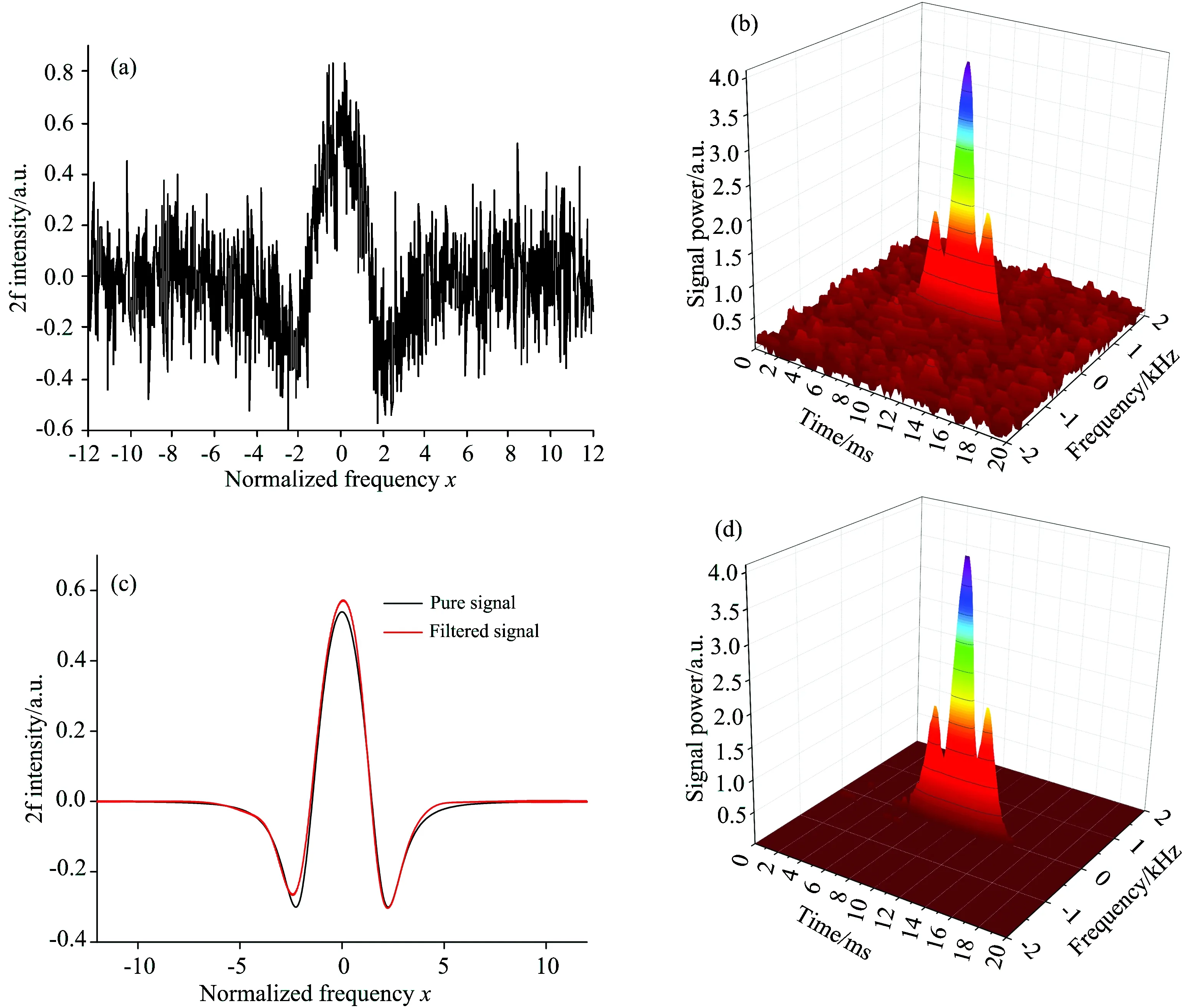
3 实验与讨论

4 结 论

