优化Savitzky-Golay滤波器的参数及其在傅里叶变换红外气体光谱数据平滑预处理中的应用

赵安新，汤晓君，张钟华, 3，刘君华

1.西安科技大学，陕西 西安 710054 2.西安交通大学电力设备电气绝缘国家重点实验室，陕西 西安 710049 3.中国计量科学研究院，北京 100013

优化Savitzky-Golay滤波器的参数及其在傅里叶变换红外气体光谱数据平滑预处理中的应用

赵安新1, 2，汤晓君2，张钟华2, 3，刘君华2

1.西安科技大学，陕西 西安 710054 2.西安交通大学电力设备电气绝缘国家重点实验室，陕西 西安 710049 3.中国计量科学研究院，北京 100013

对傅里叶变换中红外光谱数据的平滑预处理中，通常采用Savitzky-Golay滤波器的方法进行光谱数据的平滑预处理，然而Savitzky-Golay滤波器的多项式拟合阶次和窗宽等参数的合理选则始终是一个难题，并无统一的选择依据，通常在一定数值范围内，采用多组数据进行遍历尝试，最终选择一组相对较优的数据作为Savitzky-Golay滤波器的多项式拟合阶次和窗宽参数。文中探索了Savitzky-Golay滤波器的多项式拟合阶次和窗宽等参数的优化选取这一问题，并对其主要频率指标参数与多项式拟合阶次和窗宽等参数进行了定性定量分析，得出了截至频率、阻带起始点频率、第一旁瓣峰值频率及第一旁瓣峰值幅度与窗宽和阶次之间具体的计算方程表达式。随后，根据采集的中红外气体组分的光谱数据特征，依据上述计算方程式，优化计算选取多项式拟合阶次和窗宽分别为8和11时，其Savitzky-Golay滤波器的中红外气体组分的光谱数据平滑效果最优。最后通过实际采集的0.1%, 0.2%, 0.5%, 1%, 2%, 5%浓度的CH4光谱数据进行平滑预处理，在次吸收峰区域，原始光谱的折算吸光率相对最大误差和最小误差分别为17.230 5%和0.243 0%，平滑处理后的光谱的折算吸光率相对最大误差和最小误差分别为0.088 0%和0.020 6%。可见经过Savitzky-Golay滤波器进行所探索的光谱数据预处理之后其相对误差基本稳定，并且相对较低，为后期光谱数据的准确定性和定量分析奠定了基础。

Savitzky-Golay滤波器； 光谱数据预处理； 折算吸光率； 傅里叶变换红外光谱

引 言

在光谱分析数据预处理的方法中通常采用Savitzky-Golay滤波器(S-G)方法来进行原始数据的平滑与去噪[1-3]。Savitzky-Golay滤波器(S-G)方法[4]最早由Savitzky和Golay于1964年提出，其基本原理是基于最小二乘拟合，用拟合值代替原始数值，以达到去除高频噪声点，平滑原数据序列的作用。在S-G平滑滤波过程中，滤波器窗宽及多项式拟合阶次[5]决定了S-G滤波器平滑和去噪效果。多项式拟合阶次越高，能保持的中心矩越高，即保持的细节信息越多。而滤波器窗宽越大，平滑效果越好，对噪声的衰减越大。对多项式拟合阶次与滤波器窗宽的选择，即是对保持更多信号有效细节信息与滤除更多噪声信号的综合考虑，因此构造一个合适的量化指标来评价各参数下滤波器平滑的效果显得至关重要。Browne等[6]提出了一种多尺度多项式滤波器，Larivee等[7]选择将平滑后信号的信息熵作为评价标准，Phillip Barak[8]将拟合信号的残差平方和作为平滑效果的评判标准，Jakubowska等[9]将Barak提出的自适应阶次S-G滤波算法用于平滑复杂的仿真Feldberg典型伏安信号。Vivo-Truyols等[10]认为当拟合残差的自相关与仪器噪声的自相关最接近时，平滑效果最佳，此时滤波器所选窗宽为最优值。因此发展一种简单易用、适合大众的方法很重要。之前虽已有人[11-13]对S-G滤波器频率特性进行了较深入的研究，然而并未发现有人得出滤波器窗宽、多项式拟合阶次等参数与频率特性的具体量化关系，因此无法指导用户对参数进行选择，这是S-G平滑滤波器一直以来存在的缺陷。本研究从频域出发，探索了不同参数下的S-G平滑滤波器的频率特性，据此拟合出滤波器的主要频率特性指标(截止频率、阻带起始点频率、最大旁瓣峰值频率、最大旁瓣峰值幅值等指标)与阶次及窗宽的关系。以此关系式，可对实际光谱的平滑滤波需求定量选择出S-G平滑滤波器的阶次与窗宽。

1 实验部分

1.1 材料及仪器

实验采用CH4气体傅里叶红外光谱作为分析处理目标，设定样本气CH4的浓度分别为0.1%，0.2%，0.5%，1%，2%和5%。

采用Bruke公司的alpha型傅里叶变换红外光谱仪，探测器为氘代硫酸三肽DTGS检测器，扫描范围为500～4 000 cm-1，光谱分辨率为1 cm-1，谱线值为吸光度光谱。

1.2 折算吸光率

由朗伯-比耳定律(Lambert-Beer)[14-15]可知，气体在任一波数ν处的吸光度A(ν)为

(1)

式(1)中：T(ν)为波数ν处的透射率光谱值；I0为红外光透过背景(通常是空光路)的光强，可近似等于入射光强；I为红外光透过气体样品的光强；a(ν)为气体在波数ν处的吸光度系数，在不同波数处的数值不相同，但对于特定波数，可认为不变；b为光程(样品厚度)；c为气体样品浓度。

由朗伯-比耳(Lambert-Beer)定律可知任一波长光的吸收强度(吸光度)与样品中各组分的浓度(气体浓度)成正比，与光程差(气体池长度)成正比。

对于给定的光谱仪，若气体池不变，则认为光程b是恒定不变的，因此可用折算吸光率δ(ν)[16]来等价吸光率a(ν)与光程差b，即

δ(ν)=a(ν)×b

(2)

对于单组份样品，式(1)可转化为

(3)

进而可知单组份气体折算吸光率δ(ν)的计算式(4)。

(4)

理论上在特定波数ν处，气体浓度在一定范围内时，吸光率a(ν)恒定不变，对应的折算吸光率δ(ν)也不变。然而由于干涉信号在采样过程中存在信号截断，导致光谱存在能量泄露。另外，气体对红外光也会存在一定程度的散射，再加上光谱噪声的影响，会导致折算吸光率δ(ν)在光谱存在吸收的区域随着气体浓度的增加而呈现下降趋势。

2 结果与讨论

2.1 主要Savitzky-Golay滤波器频率参数分析

为探索Savitzky-Golay滤波器多项式拟合阶次与窗宽之间的时域和频域特性关系，使用计算机模拟软件，分别模拟Savitzky-Golay滤波器在多项式拟合阶次d=2, 4, 6, 8, 10, 12, 14，窗宽范围N为(d+3, 121)区间内奇数(odd)的特性指标，计算其主要频率特性指标(截止频率fc、阻带起始点频率fb、第一旁瓣峰值频率fp及第一旁瓣峰值幅度Ap)。

图1为Savitzky-Golay滤波器主要频率特性指标截止频率fc、阻带起始点频率fb、第一旁瓣峰值频率fp及第一旁瓣峰值幅度Ap与窗宽之间的关系。四种频率特性指标参数与窗宽基本都呈现指数分布形式，在一定拟合阶次下，各项指标参数随着窗宽的增大按照指数分布的形式逐渐减小，在窗宽10～40区间为其转折点，并且随着拟合阶次的增加，其转折点逐渐右移且变化越来越平缓； 在窗宽大于40的区域，各项频率指标参数变化越来越平缓； 在窗宽大于100的区域，各项频率指标参数基本不再随着窗宽改变而变化。此项特征对于根据特定的平滑和滤波对象，选择多项式拟合阶次和窗宽提供了依据，如果已知平滑对象的各项频率指标参数，可以根据此特征选定Savitzky-Golay滤波器的参数。同时，如果知道Savitzky-Golay滤波器的参数，可以确定平滑对象的各项频率指标参数。根据式(5)—式(8)计算的数据，分别拟合了Savitzky-Golay滤波器主要频率特性指标截止频率fc、阻带起始点频率fb、第一旁瓣峰值频率fp及第一旁瓣峰值幅度Ap与窗宽和阶次之间的关系方程式。

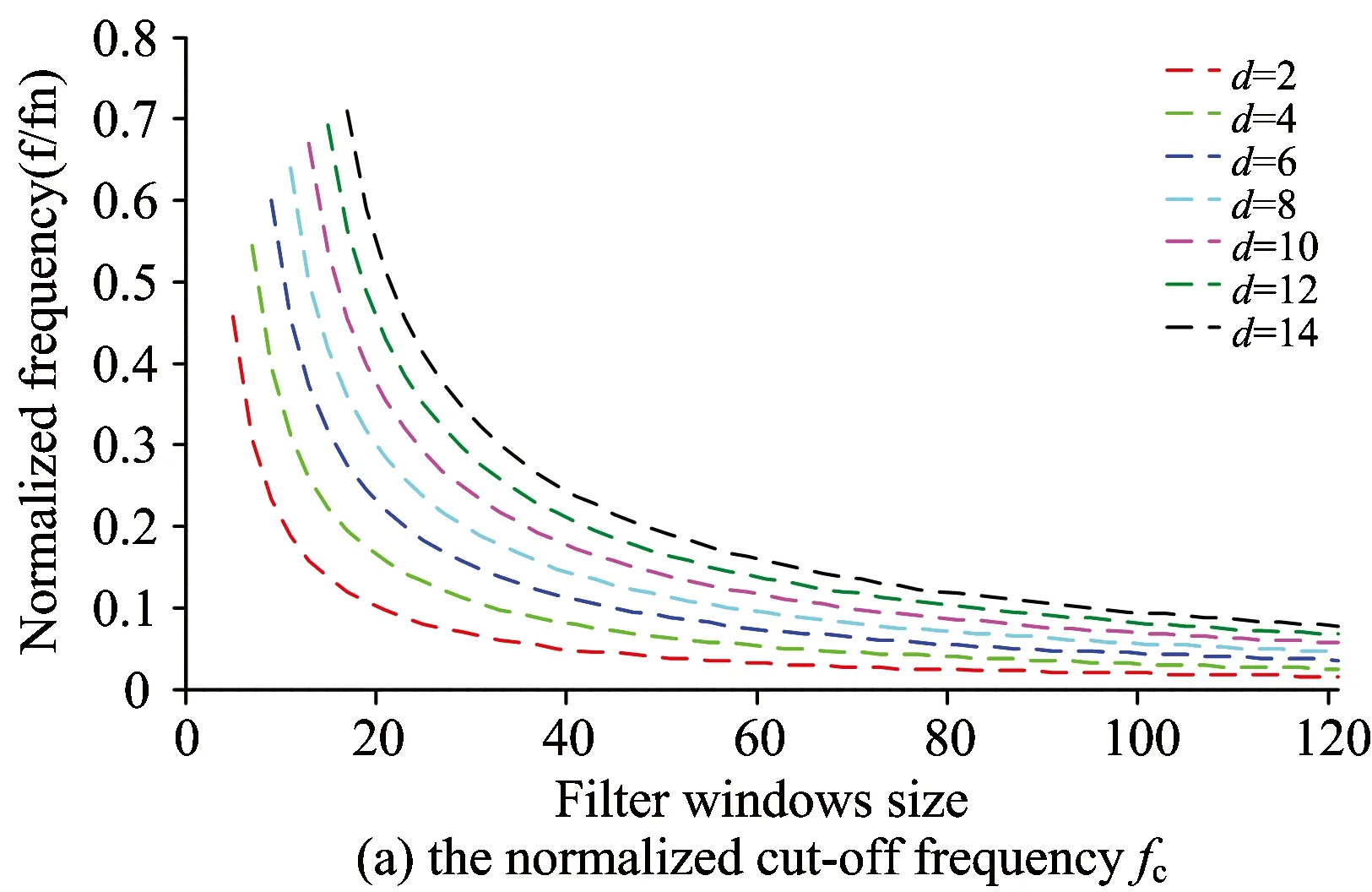
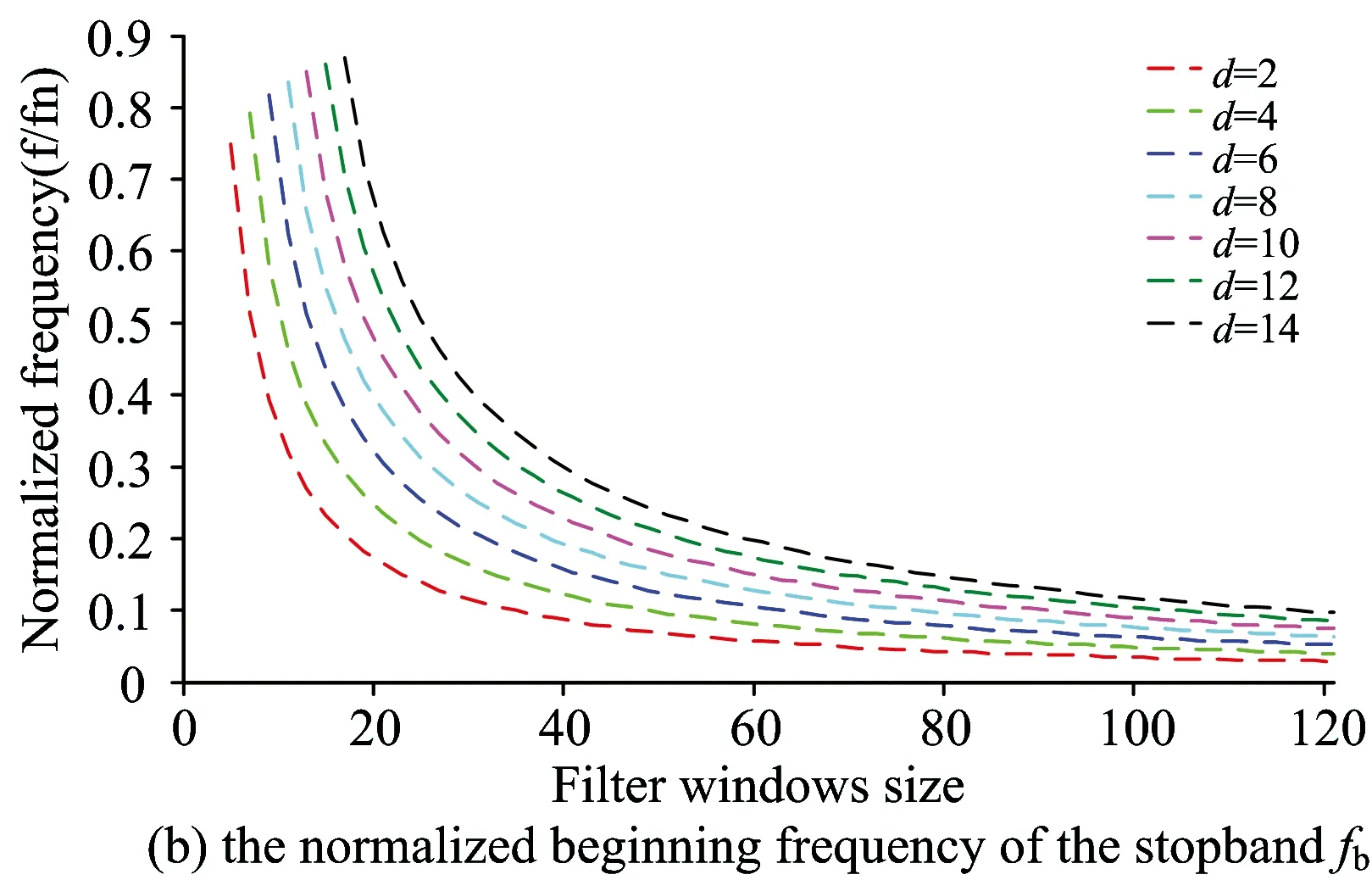
图1 Savitzky-Golay滤波器主要特性指标与窗宽N在不同多项式拟合阶次下的变换关系

(5)

(6)

(7)

(8)

2.2 傅里叶变换红外光谱数据预处理

图2为浓度分别为0.1%，0.2%，0.5%，1%，2%，5%浓度CH4气体的傅里叶变化红外吸收光谱，该光谱采用分段比基线校正方法对其进行了数据基线校正的预处理[16]，光谱经过基线校正预处理之后，其基线的漂移和部分畸变得到了一定程度的抑制。其在中红外波段主要存在两个主要的吸收区域，即是主吸收峰区域(2 850～3 200 cm-1)和次吸收峰区域(1 200～1 400 cm-1)。从主、次吸收峰处峰高随浓度的变化趋势可以看出，在此浓度范围内吸光度和浓度基本呈正比状态，初步验证了1.2节朗伯-比耳定律(Lambert-Beer)在推导折算吸光率时得出的结论。在次级吸收峰区域其正比例关系优于主吸收峰，次级吸收峰的谐波较少，主吸收峰区域的谐波较多，相互之间存在一定的干扰，因此在2.3节的计算和推导过程中采用次级吸收峰区域进行计算。

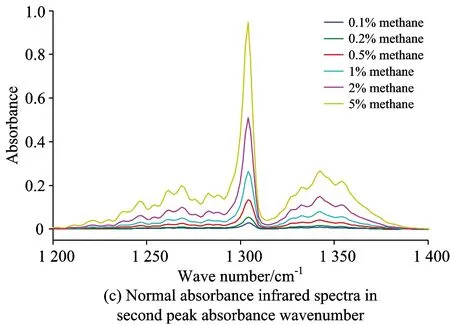
图2 经过基线校正后浓度0.1%，0.2%，0.5%，1%，2%，5%的甲烷CH4红外吸收光谱

Fig.2 Normal absorbance infrared spectra of concentration 0.1%, 0.2%, 0.5%, 1%, 2% and 5% for CH4in the region of 800～3 850 cm-1after baseline correction

2.3 光谱平滑与折算吸光度分析

以式(4)计算吸光度，0.1%, 0.2%, 0.5%, 1%, 2%和5%浓度的CH4气体在原始光谱、Savitzky-Golay平滑和去噪后光谱次吸收峰区域的折算吸光率如表1所示，表1列出了不同浓度(0.1%, 0.2%, 0.5%, 1%, 2%和5%)甲烷(CH4)目标气体在次吸收峰区域内的折算吸光率及其与相应标准浓度之间的相对误差。从标准光谱的折算吸光度计算结果来看，初步验证了研究中所的得出的结论，即不同浓度下折算吸光率相差不大，但随着浓度的增加折算吸光率逐渐减小。原始光谱浓度越小与标准光谱之间的误差越大。利用Savitzky-Golay滤波器进行平滑和去噪后，其折算吸光度与标准光谱之间的误差相对较小，基本与浓度没有特定的关系，误差维持在一定范围内，初步验证了本方法的有效性。图3为浓度为0.1%的CH4气体，经过Savitzky-Golay平滑和去噪后的傅里叶变化红外吸收光谱，从图3观察，其平滑之后在中红外波段波形基本无变化，在边界具有水汽吸收区域基本抑制了水汽的影响，同时光谱变得较平滑。Savitzky-Golay平滑和去噪后的吸收光谱和标准吸收光谱基本重合，偏差很小。同时其在次级吸收峰区域的折算吸光度分别为：25.901 7和26.248 9，标准光谱在次吸收峰区域的折算吸光率为26.272 0，其相对误差分别为1.409 5%和0.088 0%。说明平滑和滤波之后，其处理效果较好，同时在次级吸收峰其折算吸光率更能反映处理效果。而且次级吸收峰由于在低浓度范围，其吸光度和浓度的正比例关系优于主吸收峰区域，计算的结果也验证了此结论。为后期的定性和定量计算奠定了基础。

图3 经过Savitzky-Golay平滑和去噪后浓度0.1%的甲烷CH4红外吸收光谱

Fig.3 Normal absorbance infrared spectra of concentration 0.1% for CH4in the region of 800～3 850 cm-1after Savitzky-Golay smoothing and denoising

表1 不同浓度甲烷(CH4)气体在主吸收峰区域折算吸光率及其相对误差(标准光谱、原始光谱和平滑处理后光谱)

Table 1 The converted absorbance and relative error in the second peak absorption region for the different concentrations of methane CH4(standard spectra, raw sqectra and smoothing and denoising spectra)

标准光谱原始光谱处理后光谱测量值测量值相对误差/%测量值测量值0.1%27.690132.461217.230527.68440.02060.2%27.020830.762213.846427.01410.02490.5%27.068427.13420.243027.05530.04831.0%26.272025.90171.409526.24890.08802.0%25.423025.94462.051625.36930.21115.0%18.938419.25091.650218.83170.5634

3 结 论

针对傅里叶变换红外光谱数据平滑预处理的常用方法Savitzky-Golay滤波器参数的选择问题，探索了其主要频率指标参数与参数拟合阶次和窗宽之间的变化关系，提出其定量的计算方程式，为其在后续的平滑数据预处理中的应用提供依据。其次，利用实测的不同浓度的甲烷CH4光谱，采用上述结论对其进行平滑预处理。最后，利用折算吸光度对原始光谱数据和平滑处理后的光谱数据计算结果对比可知，原始光谱数据的折算吸光率相对最大误差和最小误差分别为17.230 5%和0.243 0%，平滑处理后的光谱的折算吸光率相对最大误差和最小误差分别为0.088 0%和0.020 6%。大大降低了光谱折算吸光率的计算误差，初步验证了本方法的有效性，同时为后续的光谱数据定性和定量分析奠定了基础。

[1] Zimmermann B, Kohler A.Appl.Spectrosc., 2013, 67: 892.

[2] Serafinczuk J, Pietrucha J, Schroeder G, et al.Opt.Appl., 2011, 41: 315.

[3] Staggs J.Fire Safety J, 2005, 40: 493.

[4] Gorry P A.Anal.Chem., 1990, 62: 570.

[5] Luo J W, Ying K, Bai J.Signal Process, 2005, 85: 1429.

[6] Browne M, Mayer N, Cutmore T R H.Digit Signal Process, 2007, 17: 69.

[7] Larivee R J, Brown S D.Anal.Chem., 1992, 64: 2057.

[8] Barak P.Anal.Chem., 1995, 67: 2758.

[9] Jakubowska M, Kubiak W W.Anal.Chim.Acta, 2004, 512: 241.

[10] Vivó-Truyols G, Schoenmakers P J.Anal.Chem., 2006, 78: 4598.

[11] Luo J W, Ying K, He P, et al.Digit Signal Process, 2005, 15: 122.

[12] Zuo C, Chen Q, Yu Y, et al.Opt.Express, 2013, 21: 5346.

[13] Browne M, Mayer N, Cutmore T R H.Digit Signal Process, 2007, 17: 69.

[14] Bunaciu A A, Aboul-Enein H Y, Fleschin S.Appl.Spectrosc.Rev., 2011, 46: 251.

[15] Tang X, Zhang L, Wang E, et al.Spectrosc.Spect.Anal., 2012, 32: 2730.

[16] Tang X, Wang J, Zhang L, et al.Spectrosc.Spect.Anal., 2013, 33: 334.

(Received Jan.20, 2015; accepted Apr.18, 2015)

Optimizing Savitzky-Golay Parameters and Its Smoothing Pretreatment for FTIR Gas Spectra

ZHAO An-xin1, 2，TANG Xiao-jun2，ZHANG Zhong-hua2, 3，LIU Jun-hua2

1.Xi’an University of Science and Technology, Xi’an 710054, 2.State Key Laboratory of Electrical Insulation and Power Equipment, Xi’an Jiaotong University，Xi’an 710049, 3.National Institute of Metrology, China, Beijing 100013, China

In the smoothing pretreatment for the quantitative analysis of hydrocarbon mixed gases by Fourier transform infrared analysis (FTIR), the Savitzky-Golay filter is usually used as one of the smoothing preprocessing methods in the Fourier transform infrared spectrum data smoothing pretreatment.However, the parameters of the Savitzky-Golay filter such as the polynomial order and frame size are not easy to decide.There is no one unified choice basis.Users usually adopt multiple sets in the special data set to try, and then select a set of relatively optimal data as the optimizing parameters of the Savitzky-Golay filter.The optimal selection method of the Savitzky-Golay filter parameters was explored, and the concrete calculation equations were deduced according to the relation among the normalized cut-off frequency, the normalized beginning frequency of the stopband, the normalized first side lobe peak frequency of the stopband, the normalized first side lobe peak amplitude with the polynomial order and frame size of the Savitzky-Golay filter parameters.Then when the polynomial order and frame size are set as 8 and 11 respectively according the above conclusion and the characteristics of the actual spectral data, the Savitzky - Golay filter smoothing effect is optimum.Through the acquisition the concentration of 0.1%, 0.2%, 0.5%, 1%, 2%, 5% for the actual CH4spectra, the relative maximum and minimum error of the raw spectra converted absorbance were 17.230 5% and 0.243 0% respectively, and the relative maximum and minimum error of the smooth spectra converted absorbance were 0.088 0% and 0.088 0% respectively in the second absorption peak.The relative error of converted absorbance was basically stable through the Savitzky-Golay filter after the spectral data preprocessing and it was relatively low, so, it laid a foundation for the late spectral data accurate qualitative and quantitative analysis.

Savitzky-Golay filter; Spectra pretreatment; Converted absorbance; Fourier transform infrared spectroscopy

2015-01-20，

2015-04-18

国家重大科学仪器设备开发专项(2012YQ240127)，国家自然科学基金项目(51277144)，电力设备电气绝缘国家重点实验室基金项目(EIPE11307)

赵安新，1981年生，西安科技大学博士研究生 e-mail: zhaoanxin@126.com

O433.4

A

10.3964/j.issn.1000-0593(2016)05-1340-05