基于一种混沌同步方法的多进制数字信息通信方案*

钱慧 于洪洁

（上海交通大学船舶海洋与建筑工程学院工程力学系，上海 200240）



基于一种混沌同步方法的多进制数字信息通信方案*

钱慧 于洪洁†

（上海交通大学船舶海洋与建筑工程学院工程力学系，上海 200240）

摘要本文利用基于线性系统稳定性准则的SC混沌比例投影同步方法，提出一种全新的多进制数字信息混沌保密通信方案.将多进制数字信号调制到发送端系统的雅克比矩阵和比例因子中，然后在接收端构造的子系统中判断并解调出数字信号.以传输10进制数字信息为例，利用Lorenz混沌吸引子进行数值模拟仿真，详细分析了通信过程中数字信息的同步性、安全性以及解码精度.仿真结果和数值分析证明了该多进制数字信息混沌调制方案的正确性和有效性.

关键词保密通信， 混沌调制， 数字信息， 投影同步， 雅克比矩阵

2015-01-27收到第1稿，2015-04-04收到修改稿.

*国家自然科学基金资助项目（10802030）

引言

1990年美国海军实验室的Pecora和Carroll第一次观察到混沌同步现象［1］，自此关于混沌同步方法和混沌保密通信方案的研究在国际上兴起了二十多年.混沌同步的研究是混沌安全保密通信的基础，其应用于保密通信的基本思路是，在发送端将传输信号隐藏在混沌信号中，在接收端则通过混沌特性解调出传输的有用信息.由于混沌信号非周期性、宽频带的特点，外界一般会把有用信息信号误认为是噪声信号，所以很难被窃取.要想解调出发送的信息信号，只有掌握了通信双方的同步控制约定后方能做到，达成保密效果.

自混沌同步现象被发现以来，海内外学者做了很多深入的研究，多种不同类型的同步现象相继被提出. Mainieri和Rehacek于1999年指出驱动和响应系统可以同步到一个尺度因子上［2，3］，此种同步现象即为投影同步. 2006年，Yu、Peng和Liu根据线性系统稳定性准则，提出了一种新的实现混沌投影同步的方法（SC比例投影同步方法）［4］.该方法不仅适用于三维耦合部分线性系统，同时也适用于高维甚至超混沌系统.只要配置于线性项中的雅克比矩阵A所有特征值均具有负实部，驱动系统和响应系统即可以达到投影同步.该方法中Lyapunov函数不需要构造，系统条件Lyapunov指数也不用去计算，雅克比矩阵A也可在较广范围内配置，所以此投影同步方法简单而有效.

混沌掩盖、混沌调制、混沌键控和扩频通信是目前提出和发展的四种基于混沌同步的保密通信技术. Cuomo和Oppenheim等［5］于1993年构造出了一种基于混沌掩盖技术的保密通信模拟试验电路，混沌掩盖多用于传输模拟信号.混沌键控在键控式数字通信方案中研究较多.扩频通信技术最早应用于军事通信领域.混沌调制方法于1993～1995年被提出［6］，是一种针对数字信号的通信方案，信息信号隐藏于整个混沌信号谱，对参数变化的敏感性更大，但系统的保密性得到了改善.

本文研究的重点是混沌参数调制方法.混沌参数调制是在系统某些参数中隐藏所传输的信息信号，使系统的运动轨迹在不同混沌吸引子之间变动，于接收端恢复相应的参数来提取所传输的信息信号［7］. Yang和Chua在1996年提出了一种适用一般信号调制的混沌参数调制方案［8］，并对蔡氏电路实施了混沌参数调制方案的数值仿真. Chee和Xu利用投影同步把多进制数字信息调制进比例因子中［9］，在接收端成功地解码出数字信息.文献［10］提出了一种基于统一参数混沌系统的参数调制新方法，该方法没有利用混沌同步原理，数据传输速率不受同步误差时间的限制.文献［11］提出一种多通道混沌调制模拟-信息转换结构，该结构显著提高了高稀疏度信号的重构性能.此外，最近几年国内外在混沌调制领域还出现了很多重要的新进展和新尝试［12 -15］.

本文将基于SC混沌比例投影同步方法，设计一种传输多进制数字信息的混沌参数调制方案.首先对发送端混沌系统适当分离配置出线性项和非线性项，令配置于线性项的雅克比矩阵A特征值实部均为负，然后将多进制数字信息调制到发送端系统的雅克比矩阵A和比例因子α中，从而控制输出的混沌载波信号，使其在传输过程中不停地在N个混沌信号之间来回切换，最后在接收端构造的子系统中判断并解调出数字信息.文中将利用Lorenz混沌吸引子构造10进制数字通信系统的发送端和接收端，用Matlab软件做数值模拟仿真，分析通信过程中的收敛性和误码率，验证该方法的有效性.

1 SC比例投影同步方法［4］

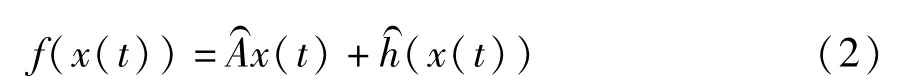
考虑一个如下描述的混沌系统：其中x（t）∈Rn是混沌系统的n维状态向量，f：Rn→Rn定义了一个n维向量场.将函数f（x（t））分解如下：其中函数x（t）是f（x（t））的线性部分（x（t））则是f（x（t））的非线性部分.然后将x（t）进行适当分离配置x（t）= Ax（t）+x（t）.这里A是满秩的常数矩阵，且配置其所有特征值均具有负实部，Ax（t）则是线性函数x（t）的剩余部分.令函数g（x （t））= Ax（t），h（x（t））=x（t）+（x（t）），则混沌

系统（1）作为驱动系统可被重新描述为：

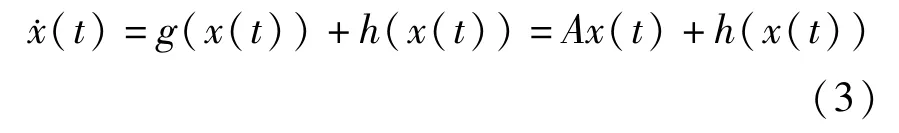
然后构造一个新的系统作为响应系统：

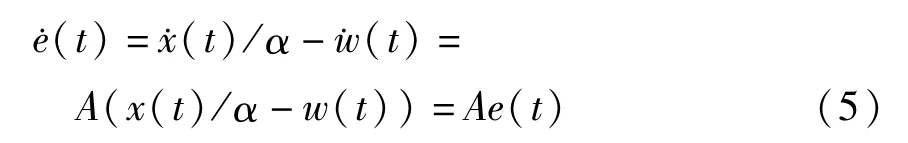
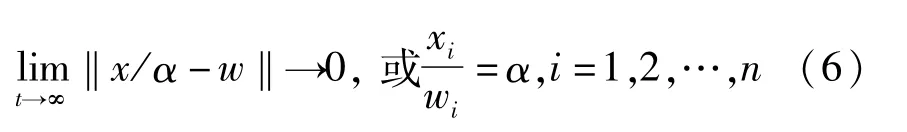
2 多进制数字信息混沌调制设计方案

对于连续的混沌系统（1），按照式（2）和（3）先将微分方程右端分离出线性项和非线性项，再根据线性部分适当配置雅克比矩阵A，并建立矩阵集合

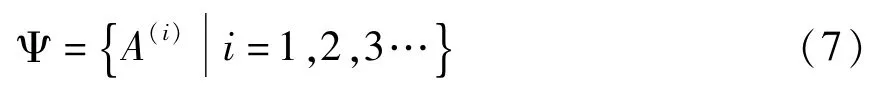
其中A（i）是由混沌系统线性部分不同元素配置出的雅克比矩阵，都是实满秩矩阵，且它们的所有特征值均具有负实部，从而保证构造的接收端子系统能够和混沌发送端系统达到同步.

建立数字集合

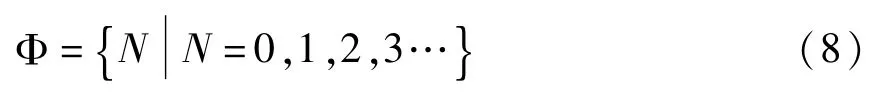
使得Ψ→Φ= H（ψ）是一一对应关系，并令比例因子α= N +1.当在通信系统发送端采用不同雅克比矩阵配置时，由式（4）可知发送端输出的混沌载波信号h（x（t））/α也是不一样的.因此只有在接收端系统的线性部分配置相同雅克比矩阵时，保密通信系统发送端和接收端才能在混沌载波信号的驱动下达到比例投影同步.因为集合Φ中的每一个数字N都对应着集合Ψ中的每一种雅克比矩阵配置A（i）和一个比例因子α，所以只要掌握了事先制定的映射规则和调制方式，便可以在通信系统的接收端解调出所传输的数字信息.

图1是M =10进制混沌调制数字通信系统示意图. m（t）是所需传输的10进制数字信息，其被调制进通信系统的发送端，控制发送端输出的混沌载波h（x（t））/α，虚线框内是构造的接收端10个子系统.对应关系有：

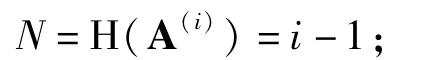
当发送端系统传输某个数字信息N时，其相应雅克比矩阵配置为A（i），比例因子α= N + 1，输出的混沌信号是h（i）（x（t））/（N +1）.在通信系统接收端，构造的10个子系统同时接收混沌驱动信号h（i）（x（t））/（N +1），子系统j的动力微分方程为：

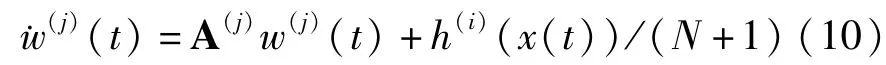
所以在数字信号N的传输期间时，接收端的10个子系统中，只有子系统j（j = i）与发送端系统达到比例投影同步，其余9个子系统j（j≠i）则无法与发送端系统同步.

对于10进制数字N，N∈m（t），由于N被调制进比例因子α：α= N +1，则在通信系统接收端中与发送端系统达到比例投影同步的第j（j = i）个子系统可解调出10进制数字信息N：^N =α- 1，^N∈^m（t），以此输出解码信息^m（t）.传输过程中的调制和解调如下：

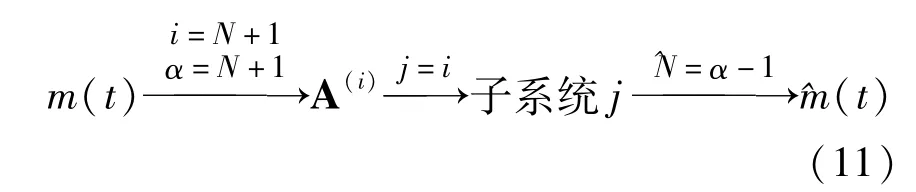
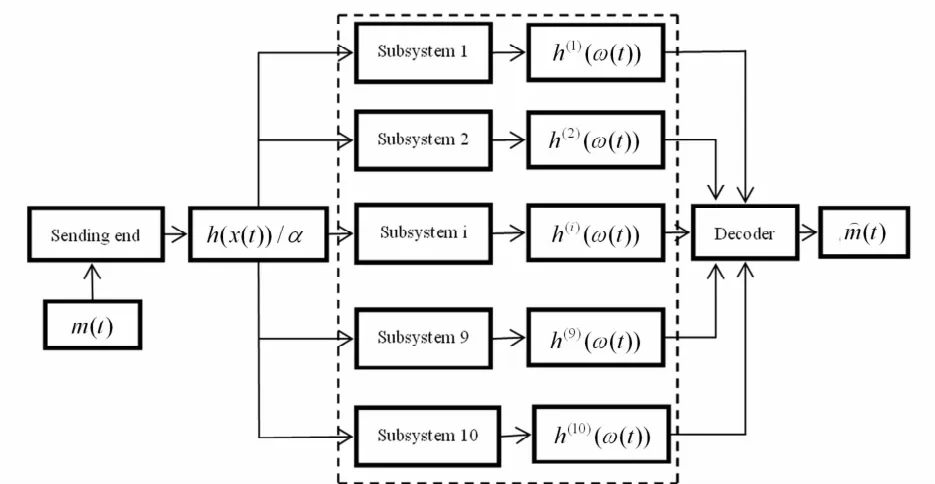
图1 10进制数字信息混沌调制通信过程示意图Fig. 1 Process of 10-ary digital communication based on chaotic modulation

从表1中可以看出，每传输一个10进制数字就等于传输了4个2进制的位码，信息传输速率是2进制数字信息传输的4倍.

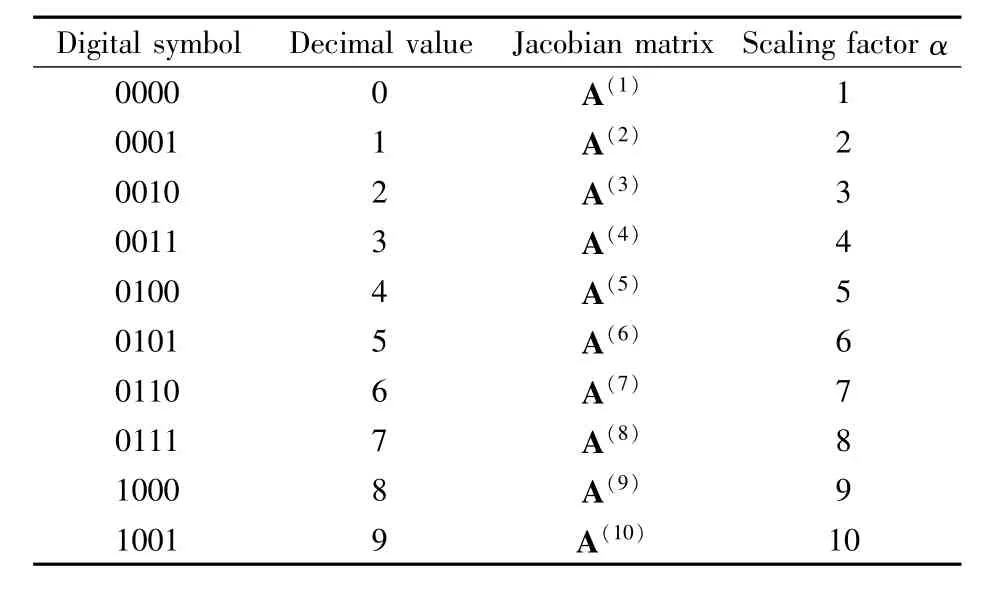
表1 10进制数字对应的2进制符号、雅克比矩阵和比例因子Table 1 Digital symbol，Jacobian matrix and scaling factor of the corresponding decimal value

3 数值仿真

利用Lorenz吸引子构造10进制数字通信系统的发送端和接收端. Lorenz混沌系统可用如下微分方程表示：

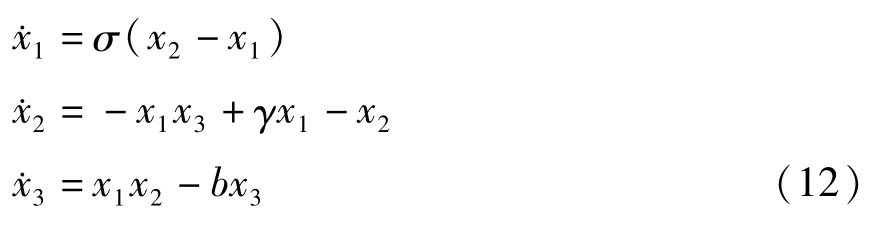
其中σ=16，γ=45. 92，b =4.

建立10进制数字信息集合

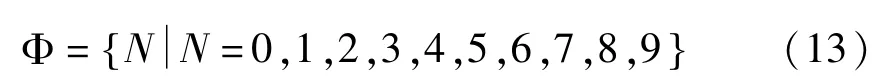
同时建立雅克比矩阵集合与相应的比例因子α集合

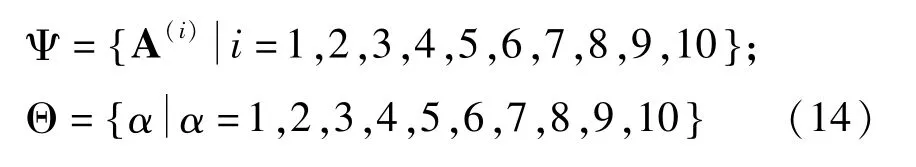
映射规则如（9）：

通信系统发送端按照（3）式分离配置为

传输的混沌载波信号为

按照方程（10）构造的10个接收端子系统为

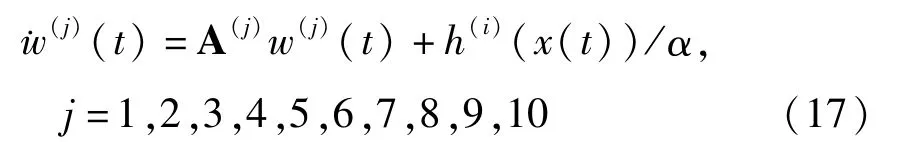
令所需传输的10进制数字信息为m（t）=［0，1，5，7，2，6，4，3，8，5，9，3］，其中mi∈Φ. m（t）中每一个数字信息持续10个时间单位.用Matlab自带的微分方程求解器ode45做数值分析时，通信系统的发送端取初始值为x0=［-2，1，5］，接收端子系统1～10分别取初始值为w0（1）=［2，-1，4］ =［-1，- 1，3］，=［2，3，4］，=［1，5，2］=［2，6，3］，=［0，1，1］=［1，4，3］，=［-3，2，-1］，w0（9）=［2，1，1］，=［1，2，3］.表2中第1列是接收端10个子系统所配置的雅克比矩阵.这10个雅克比矩阵的特征值相同，均为负实数，特征值为λ1= - 16，λ2= - 1，λ3= -4.从A（1）到A（10）矩阵元素A12以2递增，A（1）是最简单的对角型配置= 0= 18.表2的第三列是传输不同数字信息时发送端系统输出的混沌载波信号h（i）（x（t））/α，在传输过程中混沌信号在这10个不同载波信号之间来回切换.

表2 不同配置的雅克比矩阵、比例因子和混沌传输信号Table 2 Jacobian matrix，scaling factor and transmitted chaotic signal with different configuration

图2显示的是在通信过程中，接收端10个子系统与发送端系统的投影同步误差随时间发展历程.图2（a）显示接收端子系统1在时间0＜t＜10内与发送端系统状态变量投影同步误差迅速收敛为0，达到投影同步，而在其它时间范围内投影同步误差为混沌解，不为0.从另外9张图中也可以看出在时间0＜t＜10时，子系统i（i =2，3，4，5，6，7，8，9）与发送端系统不同步，说明在时间0＜t＜10内所传输的数字信息是N =0.图2（b）显示接收端子系统2在时间10＜t＜20与发送端系统达到投影同步，在其它时间范围内不同步.另外9张图中也可发现在时间10＜t＜20内，子系统i（i =1，3，4，5，6，7，8，9）与发送端系统不同步，说明在时间10 ＜t＜20内所传输的数字信息是N = 1.图2（c）显示接收端子系统3只有在时间40＜t＜50时与发送端系统达到投影同步，且在此时间范围内其余子系统i（i = 1，2，4，5，6，7，8，9）与发送端系统不同步，说明在时间40＜t＜50内所传输的数字信息是N =2.同上述分析，从图2（d）可以判断出在时间70＜t＜80∪110＜t＜120内，所传输的数字信息是N =3.图2（e）可判断出在时间60＜t＜70内，所传输的数字信息是N =4.图2（f）可判断出在时间20 ＜t＜30∪90＜t＜100内，所传输的数字信息是N =5.图2（g）可判断出在时间50＜t＜60内，所传输的数字信息是N =6.图2（h）可判断出在时间30＜t＜40内，所传输的数字信息是N =7.图2（i）中可判断出在时间80＜t＜90内，所传输的数字信息是N =8.图2（j）中可判断出在时间100＜t＜110内，所传输的数字信息是N =9.将以上分析结果与图3 （a）所示传输的10进制数字信息m（t）作比较，发现接收端没有误码输出.

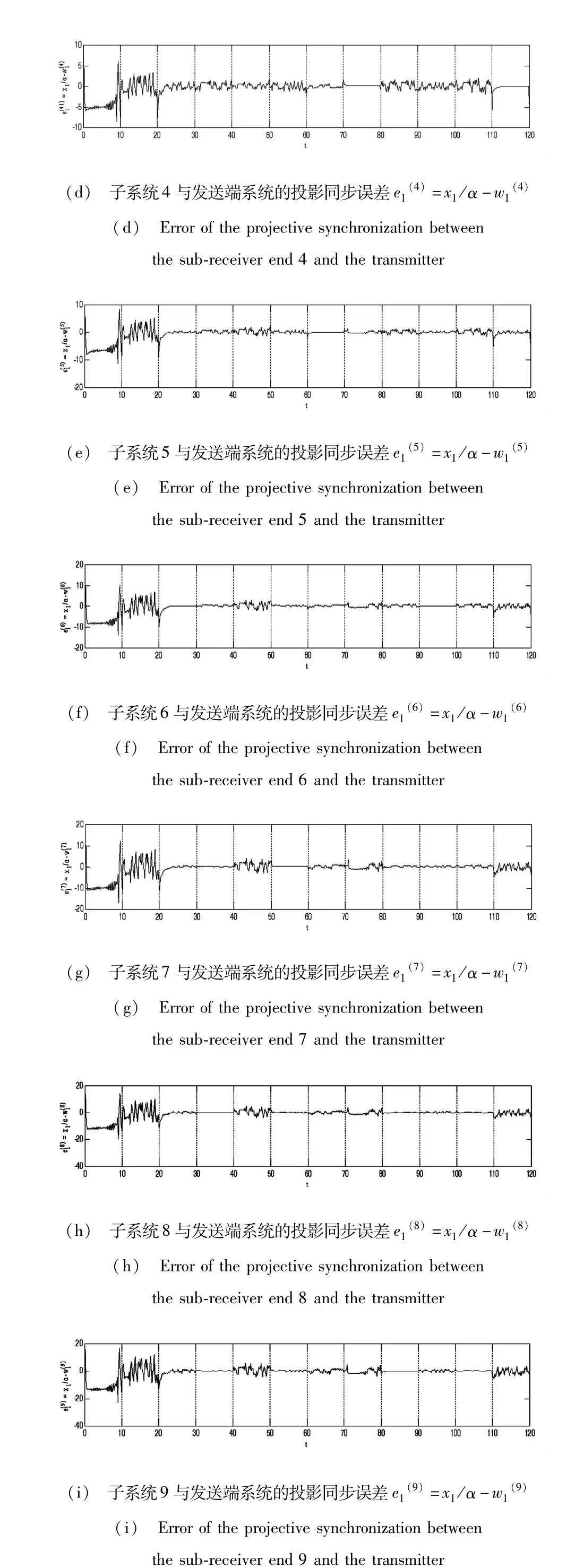
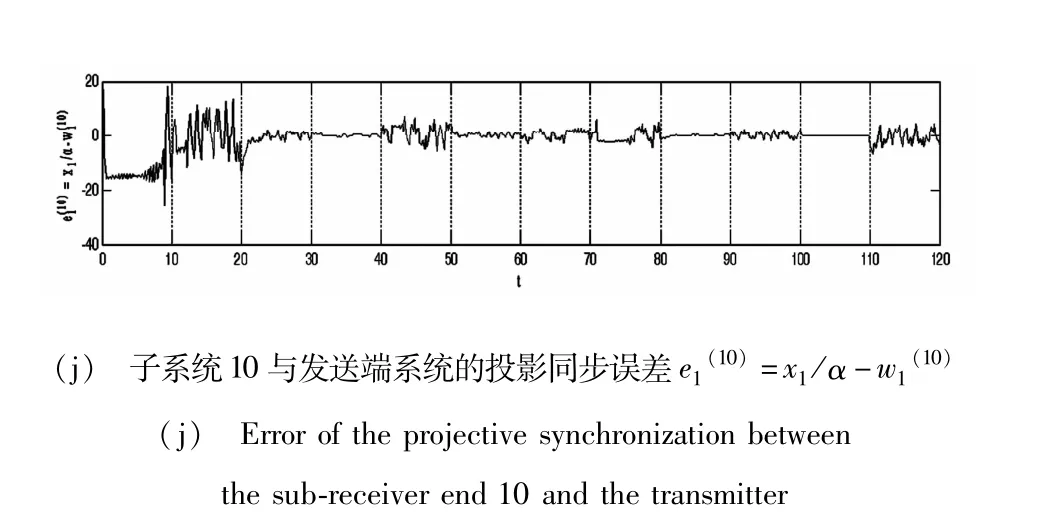
图2 通信系统接收端10个子系统与发送端投影同步误差时间历程图Fig. 2 Error of the projective synchronization between 10 sub-receiver ends and the corresponding transmitter

基于映射规则（9）解调出数字信息N：^N =α-1，^N∈^m（t）.图3展示了传输的数字信息和解码信息的对照图.图3（a）显示的是所传输的10进制数字信息m（t），图3（b）显示的是解调后的数字信息^m（t）.将这两张图对比可以看出解调数字信息^m（t）与传输数字信息m（t）符合的很好，当传输数字信息发生改变的时候，解码信息从前一个数字信号经过一段很短的时间后收敛到后一个数字信号.由此也可以说明利用Lorenz混沌吸引子构造的数字通信系统，对于传输多进制数字信息的解码过程快，误码率低，精度高.

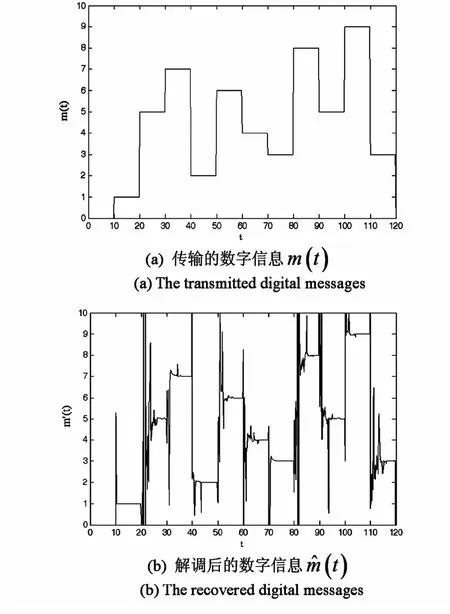
图3 解码信息^m（t）与传输信息m（t）时间历程图Fig. 3 The time history of recovered and transmitted digital messages

图4所示的是发送端输出信号h（i）（x（t））/α的第三分量h3（i）（x（t））/α，可以看出在信道中传输的信号h（i）（x（t））/α曲线，在时间域中没有稳定的幅值和周期，毫无规律可循，无法用确定的函数表示，属于混沌信号.传输信号的混沌特性提高了数字通信系统的安全保密性.

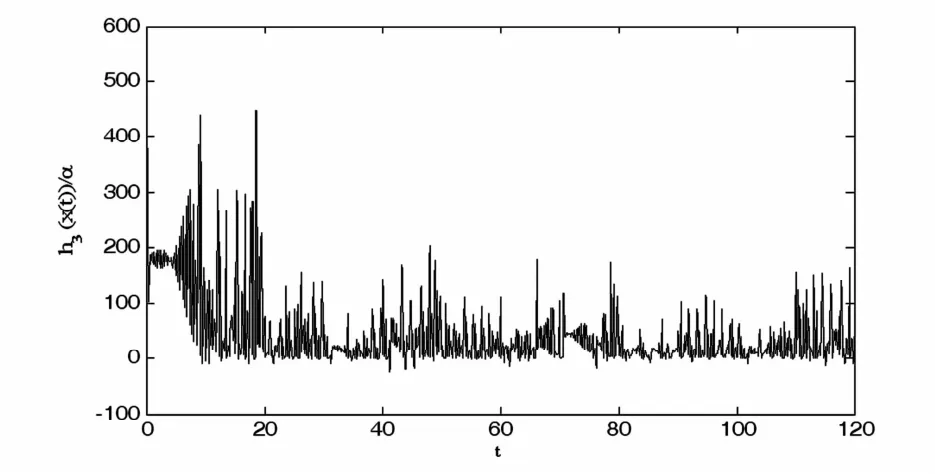
图4 通信系统发送端的输出信号h3（i）（x（t））/αFig. 4 The transmitted signal of the sub-receiver ends

4 结论

本文利用基于线性系统稳定性准则的SC混沌比例投影同步方法，设计了一种全新的多进制数字信息混沌保密通信方案.该方法在发送端系统的雅克比矩阵和比例因子中分别调制进所需传输的多进制数字信号，制定了对应的映射规则，于通信系统接收端的子系统中解调出数字信号.文中以Lorenz混沌吸引子构造了10进制数字通信系统，数值模拟发现，发送端输出信号不仅是混沌信号，而且在传输不同的数字信息时，输出信号在多个不同的混沌信号之间来回切换，增加了信息传输过程中的安全性，提高了系统的保密性.仿真结果表明，当传输某个数字码元时，发送端和对应子系统的投影同步误差迅速收敛为0，而其余子系统则与发送端的同步误差是混沌解，同时解调信息图与传输信息图也符合的很好，证明该通信系统对多进制数字信息的解码过程很快，没有误码输出，解码精度高.

参 考 文 献

1 Pecora L M，Corroll T L. Synchronization in chaotic system. Physical Review Letters，1990，64：821～824

2 Manieri R，Rehacek J. Projective synchronization in threedimensional chaotic systems. Physical Review Letters，1999，82：3042～3045

3 Xu D L，Li Z. Controlled projective synchronization in nonpartially-linear chaotic systems. International Journal of Bifurcation and Chaos，2002，12（6）：1395

4 Yu H J，Peng J H，Liu Y Z. Projective synchronization of unidentical chaotic systems based on stability criterion. International Journal of Bifurcation and Chaos，2006，16（4）：1049～1056

5 Cuomo K M，Oppenheim A V. Circuit implementation of synchronized chaos with applications to communications. Physical Review Letters，1993，71（1）：65～68

6 Parlitz U. Estimating model parameters from time series by auto-synchronization. Physical Review Letters，1996，76 （8）：1232～1235

7 杨志民，熊丽，张新国等.基于Lorenz系统的混沌调制保密通信的电路实现.西北师范大学学报，2010，46（2）：40～48（Yang Z M，Xiong L，Zhang X G，et al. Curcuit implementation of chaos modulation secure communication based on Lorenz chaotic system. Journal of Northwest Normal University，2010，46（2）：40～48（in Chinese））

8 王国红.基于变形蔡氏电路的混沌掩盖保密通信研究.空军工程大学学报（自然科学版），2005，6（4）：49～62 （Wang G H. Design of network management structure based on mobile agent technology . Journal of Air Force Engineering University（Natural Science Edition），2005，6 （4）：49～62（in Chinese））

9 Chee C Y，Xu D. Chaos based M-ary digital communication technique using controlled projective synchronization. IEE Proceedings-Circuits Devices and Systems，2006，153 （4）：357～360

10 廖旎焕，王晖，高金峰.基于统一混沌系统的参数调制新方法.电路与系统学报，2012，17（4）：95～98（Liao N H，Wang H，Gao J F. A new parameter modulation method based on the unified chaotic system. Journal of Curcuits and Systems，2012，17（4）：95～98（in Chinese））

11 陈胜垚，席峰，刘中.多通道混沌调制模拟-信息转换.电子与信息学报，2014，36（1）：152～157（Chen S Y，Xi F，Liu Z. Multi-channel chaotic modulation for analogto-information conversion. Journal of Electronic & Information Technology，2014，36（1）：152～157（in Chinese））

12 Dwivedi A，Kumar M A，Dwivedi S. Adaptive synchronization of diffusion Lorenz systems and secure communication of digital signals by parameter modulation. IET Communication，2012，6（13）：2016～2026

13 朱立岗，沈传文，朱少平.互变参数双混沌调制SPWM波生成原理及实现方法.中国电机工程学报，2014，34 （30）：5335～5341（Zhu L G，Shen C W，Zhu S P. Principle and realization of chaotic SPWM modulation based on double-chaotic sequence with mutual changing parameters. Proceedings of the CSEE，2014，34（30）：5335 ～5341（in Chinese））

14 Dwivedi A，Kumar M A，Dwivedi S. Chaotic communication using Pecora Carroll complete replacement and parameter modulation without controller. Allahabad：IEEE，2014：1～4

15 Chan H J，Heung G R. Design of chaotic CDSK modulation system using different chaotic maps. PyeongChang：IEEE，2013：222～226

Received 27 January 2015，revised 04 April 2015.

*The project supported by the National Natural Science Foundation of China（10802030）

M-ARY DIGITAL COMMUNICATION TECHNIQUEBASED ON A CHAOTIC SYNCHRONIZATION METHOD*

Qian Hui Yu Hongjie†
（Department of Engineering Mechanics，School of Naval Architecture，Ocean and Civil Engineering，Shanghai Jiao Tong University，Shanghai 200240，China）

AbstractA new communication technique of transmitting M-ary digital signals using projective synchronization based on stability criterion is proposed in this paper. At the sender，M-ary digital signals are modulated into Jacobian matrix and the scaling factor of chaotic system. The digital signals are decoded in the corresponding subsystem constructed at the receiver end. Lorenz attractor is taken as an example to simulate the process of transmitting decimal digital signals by chaotic modulation. Numerical analysis shows that the communication system has higher transmission rate and decoding accuracy for the digital symbols without increasing complexity. The security and effectiveness of the proposed technical scheme is validated through the numerical investigation.

Key wordssecure communication， chaotic modulation， digital signal， projective synchronization， Jacobian matrix

DOI：10. 6052/1672-6553-2015-039

通讯作者†E-mail：yuhongjie@ sjtu. edu. cn

Corresponding author†E-mail：yuhongjie@ sjtu. edu. cn