混沌振子在滚动轴承故障特征提取中的应用*

李岭阳 王华庆徐新韬 杨晓

（北京化工大学机电工程学院，北京 100029）



混沌振子在滚动轴承故障特征提取中的应用*

李岭阳 王华庆†徐新韬 杨晓

（北京化工大学机电工程学院，北京 100029）

摘要滚动轴承的故障信号往往是微弱的周期信号，而混沌振子对特定频率的微弱周期信号十分敏感，可以有效地检测出故障信号.介绍了混沌振子的数学模型和基本检测原理，以及策动力临界阈值的确定方法.将混沌振子检测法应用于滚动轴承外圈、内圈和滚动体故障信号的检测中，通过输出相图的变化来判断故障信号是否存在，有效地实现了对滚动轴承故障信号的检测.

关键词混沌振子， 滚动轴承， 不变矩， 微弱信号， 故障特征提取

2015-02-08收到第1稿，2015-05-06收到修改稿.

*国家自然科学基金资助项目（51375037）、教育部新世纪优秀人才支持计划（NCET-12-0759）

引言

滚动轴承的效率高，摩擦阻力小，装配方便，润滑易实现，因此它在机械设备尤其是旋转机械中使用非常普遍.由于载荷、安装、润滑等因素的影响，滚动轴承会产生很多不同的故障，它的运行状态会直接影响到整个机械设备的功能，因此对滚动轴承的故障进行诊断非常重要，而滚动轴承的振动信号中通常都含有大量的噪声，因此对微弱信号检测方法的研究十分有必要.

文献［1］利用变步长随机共振方法对滚动轴承故障信号进行了检测.文献［2］对基于Duffing振子的随机共振现象进行了研究.文献［3］将形态滤波与稀疏分量分析结合起来对滚动轴承复合故障进行了分离.

混沌振子是一种常用的非线性的微弱信号检测方法，它以输出相图的变化来反映信号中是否存在待检测频率.在机械故障诊断领域中，混沌振子检测方法已经成为轴承故障［4 -6］、齿轮故障［7 -8］、不对中故障、转子碰磨故障［9］等的重要检测方法.

本文介绍了混沌振子的基本原理和检测方法，并将其应用于滚动轴承外圈、内圈和滚动体的故障特征提取中.

1 基于混沌振子的检测方法

1. 1 混沌振子的数学模型与基本检测原理

混沌振子常采用Holmes型Duffing方程作为检测器［4 -5，7，10 -11］，其形式如下［4 -5，7］

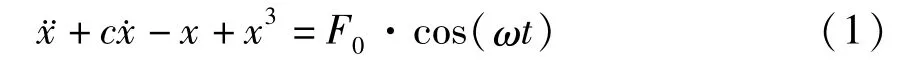
令˙x = y，取t =ω0τ，再用t代替τ，并且加入被检测的微弱周期信号和外部噪声，则对应的状态方程是

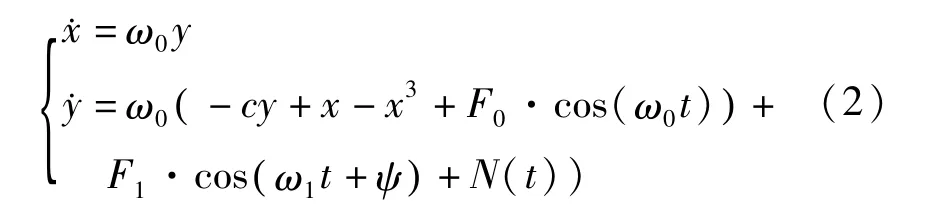
其中F0是周期性策动力的振幅，ω0是内部周期性策动力的角频率，F1是待检测周期信号的幅值，ω1是待检测周期信号的角频率，ψ是待检测周期信号的初始相位，N（t）是服从正态分布的高斯白噪声，c 是Duffing振子的阻尼常数.

如果固定c，让F0从0逐渐增加到超过某个确定的临界值并继续增加到另一个临界值，那么Duffing振子在相空间中的状态变化规律将会是：小尺度周期状态→混沌状态→大尺度周期状态.

将混沌振子输出相图从混沌状态向大尺度周期状态转变的临界值记为Fr，即当策动力的幅值大于Fr时，混沌振子输出相图就会从混沌状态变为大尺度周期状态.

因此在进行滚动轴承故障信号检测时，首先设定系统周期性策动力F0等于临界值Fr，并使内部周期性策动力的角频率ω0等于滚动轴承故障特征频率ω1，然后将滚动轴承信号加入混沌振子系统中，如果信号中含有故障特征频率ω1，那么将会有有F0+ F1Fr，此时，混沌振子输出相图将从混沌状态向大尺度周期状态转变，而如果信号中不含有故障特征频率，输出相图将会保持混沌状态不变.因此，通过混沌振子输出相图状态的变化情况就可以判断滚动轴承是否发生故障.

1. 2 混沌振子临界值Fr的确定

本文通过零输入条件下混沌振子输出相图HU不变矩的二阶不变矩φ1［4 -5］随策动力F0的关系曲线得到F0的临界值Fr.

以待检测频率为20Hz为例，在输入信号为零的条件下，将内部周期性策动力的频率设为20Hz，采样频率取1000Hz，采样点数取8000，阻尼常数c 取0. 5，不断地增加策动力的幅值，其步长为0. 01，作出输出相图的二阶不变φ1随策动力F0变化的关系曲线如图1所示.

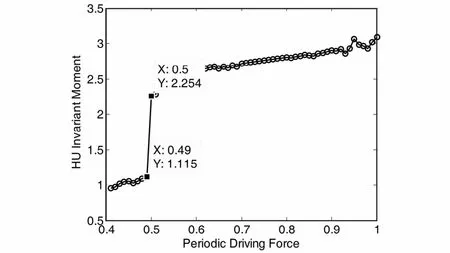
图1 零输入条件下不变矩随策动力变化的趋势图Fig. 1 HU invariant moment - periodic driving force relationship under the condition of zero input

从图1可以看出，随着策动力的增加，不变矩会在两个范围内波动.当F0≤0. 49时，不变矩的值会在［0. 5，1. 5］之间变化，当F0≥0. 50时，不变矩的值会在［2，3. 5］之间变化.在F0=0. 50处，不变矩的值发生了突变，因此，F0=0. 49是该突变的临界值记为Fr.

2 滚动轴承故障检测实例

本实验所用数据来自于如图2所示的风机实验设备主轴轴承，故障信号采用NF EZ7510数据采集设备采集，所用传感器为加速度传感器，主轴工作转速为800r/ min，采样频率为100KHz，采样时间约为10s.

具体的故障信号检测流程如图3所示.

2. 1 滚动轴承外圈故障的检测

外圈故障轴承采用NSK NF206W轴承，经计算其故障特征频率为72. 5Hz.

图2 风机实验设备外形图Fig. 2 View of fan laboratory equipment

图3 滚动轴承故障信号检测流程图Fig. 3 The flow chart of rolling bearing

阻尼系数c =0. 5，系统周期性策动力频率设为与检测频率相等，即72. 5Hz，根据前面介绍的混沌振子临界值Fr的确定方法，取策动力增长步长为0. 01，得到零输入条件下混沌振子输出相图的二阶不变矩φ1随策动力F0变化的趋势图如图4所示.

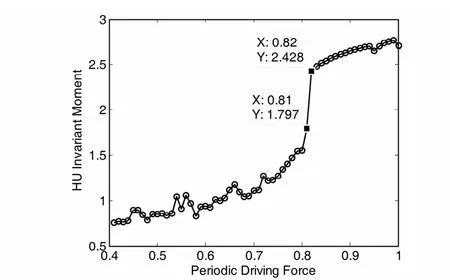
图4 零输入条件下HU不变矩随周期性策动力变化的趋势图Fig. 4 HU invariant moment - periodic driving force relationship under the condition of zero input

观察图4，可以看出在F0=0. 82处，不变矩的值发生了突变，因此，根据前面介绍的理论，可以判断F0=0. 81是该突变的临界值记为Fr.现在将系统策动力设为F0=0. 81，保持其它参数不变，作出加入信号前的混沌振子输出相图如图5所示.

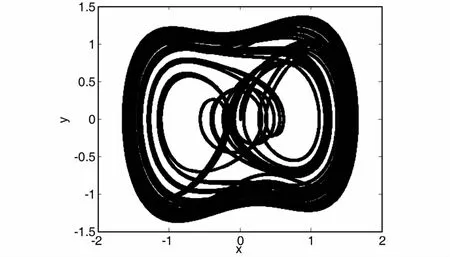
图5 F0=0. 81时加入外圈故障信号前的混沌振子输出相图Fig. 5 Output phase diagram of the chaotic oscillator before inputting the outer ring fault signal when F0=0. 81

从图5中可以看出不加输入信号时，混沌振子输出相图处于混沌状态.现在将采集到的滚动轴承外圈故障信号加入混沌振子系统中，作出混沌振子输出相图如图6所示.

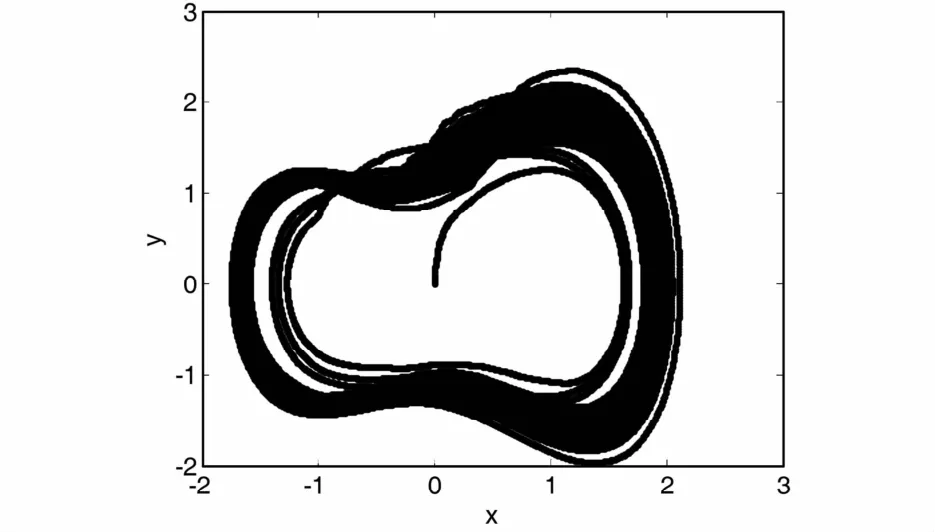
图6 F0=0. 81时加入外圈故障信号后的混沌振子输出相图Fig. 6 Output phase diagram of the chaotic oscillator after inputting the outer ring fault signal when F0=0. 81

从图6中可以看出加入外圈故障信号之后输出相图转变为了大尺度周期状态，根据前面介绍的理论，可以判断输入信号中包含有待检测频率成分，即含有72. 5Hz的频率成分.

2. 2 滚动轴承内圈故障的检测

内圈故障轴承采用NSK NU206EW轴承，经计算其故障特征频率为103. 4Hz.

阻尼系数c =0. 5，系统周期性策动力频率设为与检测频率相等，即103. 4Hz，取策动力增长步长为0.01，作出零输入条件下混沌振子输出相图的二阶不变矩φ1随策动力F0变化的趋势图如图7所示.

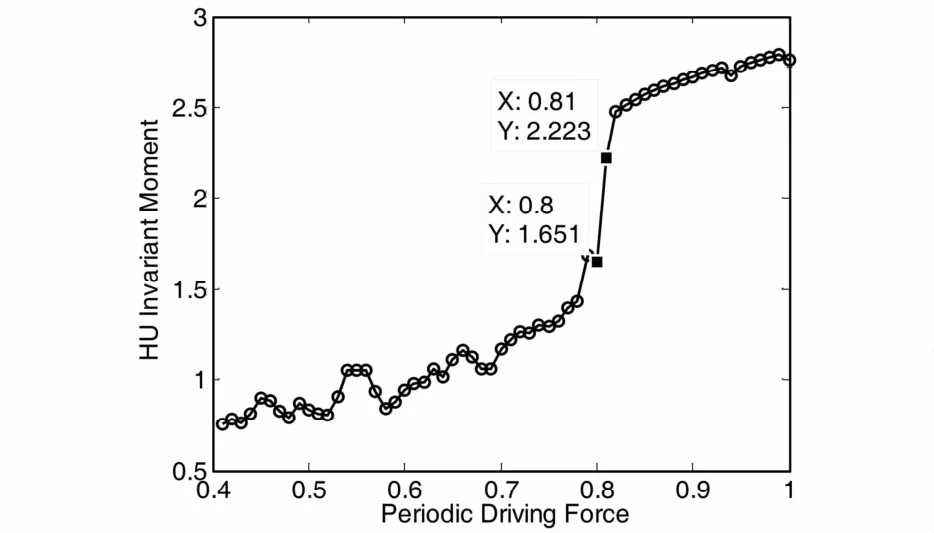
图7 零输入条件下HU不变矩随周期性策动力变化的趋势图Fig. 7 HU invariant moment-periodic driving force relationship under the condition of zero input

观察图7，可以看出在F0=0. 81处，不变矩的值发生了突变，因此，根据前面介绍的理论，可以判断F0=0. 8是该突变的临界值记为Fr.现在将系统策动力设为F0= 0. 8，保持其它参数不变，作出加入信号前的混沌振子输出相图如图8所示.

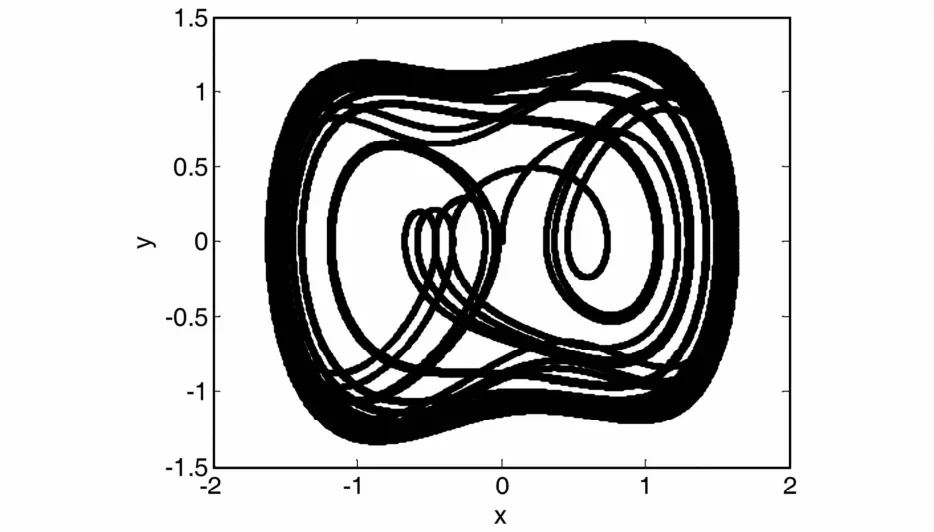
图8 F0=0. 8时加入内圈故障信号前的混沌振子输出相图Fig. 8 Output phase diagram of the chaotic oscillator before inputting the inner ring fault signal when F0=0. 8

从图8中可以看出不加输入信号时，混沌振子输出相图处于混沌状态.现在将采集到的滚动轴承内圈故障信号加入混沌振子系统中，作出混沌振子输出相图如图9所示.

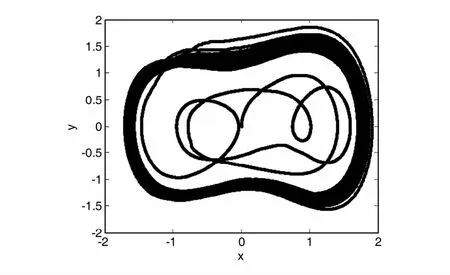
图9 F0=0. 8时加入内圈故障信号后的混沌振子输出相图Fig. 9 Output phase diagram of the chaotic oscillator after inputting the inner ring fault signal when F0=0. 8

从图9中可以看出加入内圈故障信号之后输出相图转变为了大尺度周期状态，根据前面介绍的理论，可以判断输入信号中包含有待检测频率成分，即含有103. 4Hz的频率成分.

2. 3 滚动轴承滚动体故障的检测

滚动体故障轴承采用NSK NU206EW轴承，经计算其故障特征频率为79. 6Hz.

阻尼系数c =0. 5，系统周期性策动力频率设为与检测频率相等，即79. 6Hz，取策动力增长步长为0. 01，作出零输入条件下混沌振子输出相图的二阶不变矩φ1随策动力F0变化的趋势图如图10所示.

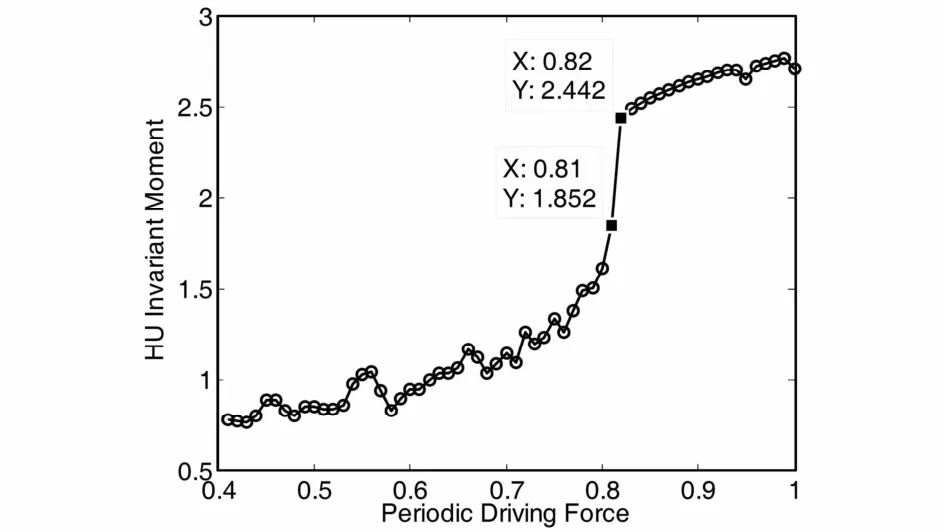
图10 零输入条件下不变矩随策动力变化的趋势图Fig. 10 HU invariant moment-periodic driving force relationship under the condition of zero input

观察图10，可以看出在F0= 0. 82处，不变矩的值发生了突变，因此，根据前面介绍的理论，可以判断F0=0. 81是该突变的临界值记为Fr.现在将系统策动力设为F0=0. 81，保持其它参数不变，作出加入信号前的混沌振子输出相图如图11所示.

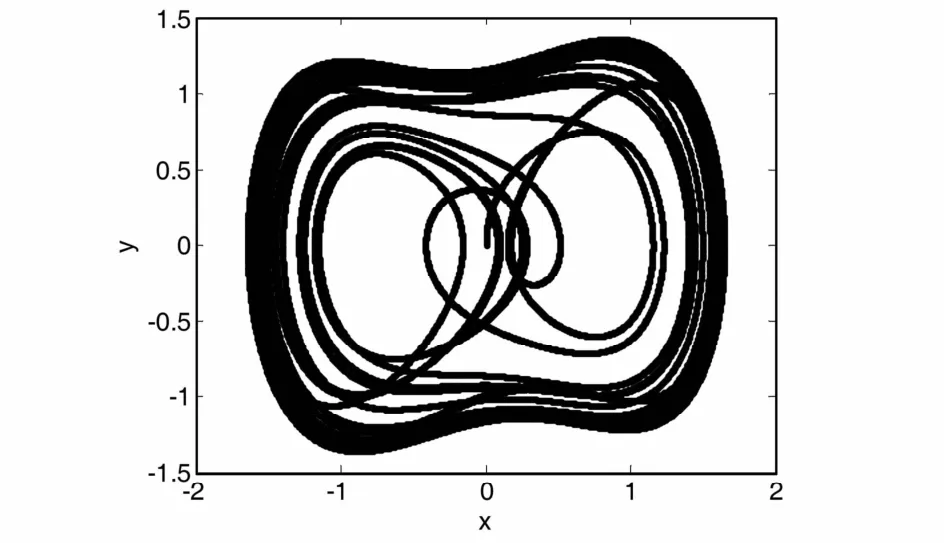
图11 F0=0. 81时加入滚动体信号前的混沌振子输出相图Fig. 11 Output phase diagram of the chaotic oscillator before inputting the rolling element fault signal when F0=0. 81

从图11中可以看出不加输入信号时，混沌振子输出相图处于混沌状态.现在将采集到的滚动轴承滚动体故障信号加入混沌振子系统中，作出混沌振子输出相图如图12所示.

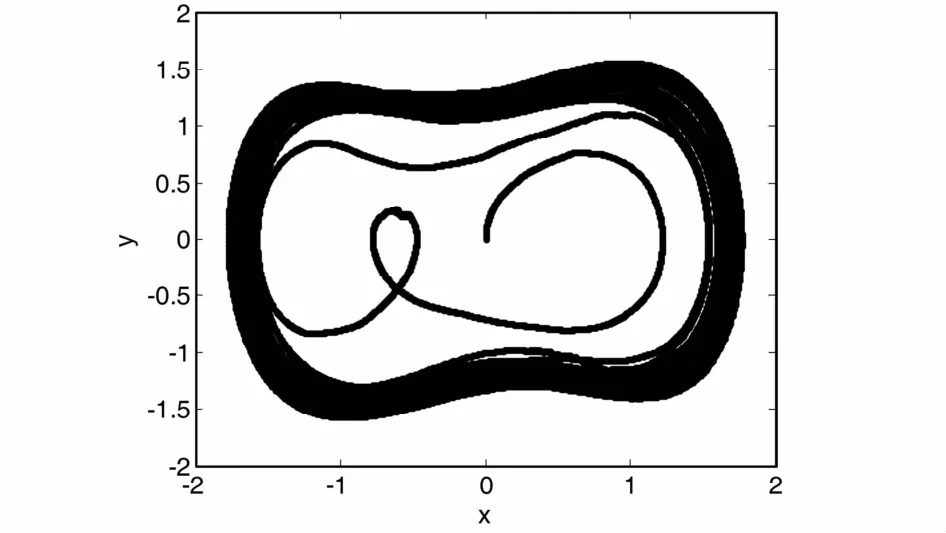
图12 F0=0. 81时加入滚动体信号后的混沌振子输出相图Fig. 12 Output phase diagram of the chaotic oscillator after inputting the rolling element fault signal when F0=0. 81

从图12中可以看出加入滚动体实验信号以后，输出相图转变为了大尺度周期状态，这说明输入信号中包含有待检测频率成分，即含有79. 6Hz的频率成分.

3 结论

滚动轴承的故障信号往往是微弱的周期信号，而混沌振子是一种常用的非线性的微弱信号检测方法，它通过输出相图的变化来判断待检测信号是否存在.本文阐述了混沌振子的基本原理和检测方法，介绍了混沌振子策动力临界值的确定方法，并将混沌振子检测方法应用于滚动轴承外圈、内圈和滚动体故障特征的提取中，有效地实现了对滚动轴承故障信号的检测.

参 考 文 献

1 张仲海，王太勇，王多，林锦州，蒋永翔.采用粒子群算法的自适应变步长随机共振研究.振动与冲击，2013，32 （19）：125～130（Zhang Z H，Wang T Y，Wang D，Lin J Z，Jiang Y X. Self-adaptive step-changed stochastic resonance using particle swarm optimization. Journal of Vibration and Shock，2013，32（19）：125～130（in Chinese））

2 赵志宏，杨绍普，刘永强.基于Duffing振子的随机共振研究.动力学与控制学报，2014，12（2）：160～164（Zhao Z H，Yang S P，Liu Y Q. Study of stochastic resonance based on Duffing oscillator. Journal of Dynamics and Control，2014，12（2）：160～164（in Chinese））

3 李豫川，伍星，迟毅林，刘畅.基于形态滤波和稀疏分量分析的滚动轴承故障盲分离.振动与冲击，2011，30 （12）：170～174（Li Y C，Wu X，Chi Y L，Liu C. Blind separation for rolling bearing faults based onmorphological filtering and sparse component analysis. Journal of Vibration and Shock，2011，30（12）：170～174（in Chinese））

4 马海龙，胥永刚.复杂机电设备微弱特征提取与早期故障诊断方法研究.北京：北京工业大学，2011（Ma H L，Xu Y G. Research on the method of weak feature extraction and incipient fault diagnosis for complex electromechanical equipment. Beijing：Beijing University of Technology，2011（in Chinese））

5 何金群，胥永刚，崔玲丽，高立新，侯建国.基于不变矩的Duffing相位图的自动识别.噪声与振动控制，2008，28 （5）：80～82（He J Q，Xu Y G，Cui L L，Gao L X，Hou J G. Automatic identification of Duffing phase diagram based on moment invariant. Noise and Vibration Control，2008，28（5）：80～82（in Chinese））

6 张勇，纪国宜.基于混沌振子和小波理论的轴承故障诊断方法.轴承，2010，（5）：53～55（Zhang Y，Ji G Y. Fault diagnosis method of rolling bearings based on chaotic oscillator and wavelet theory. Bearing，2010，（5）：53～55 （in Chinese））

7 Li C，Qu L. Applications of chaotic oscillator in machinery fault diagnosis. Mechanical Systems and Signal Processing，2007，21（1）：257～269

8 李崇晟，屈梁生.齿轮早期疲劳裂纹的混沌检测方法.机械工程学报，2006，41（8）：195～198（Li C S，Qu L S. Chaotic detection method of gear early-stage fatigue crack. Chinese Journal of Mechanical Engineering，2006，41（8）：195～198（in Chinese））

9 陈敏，胡茑庆，温熙森.混沌振子在转子系统早期碰摩故障检测中的应用.国防科技大学学报，2001，23（1）：36 ～39（Chen M，Hu N Q，Wen X S. The application of chaotic oscillators in early detecting rub-impact fault of rotor system. Journal of National University of Defense Technology，2001，23（1）：36～39（in Chinese））

10 徐艳春，杨春玲.基于混沌振子的微弱信号检测技术研究.电气应用，2008，27（8）：38～41（Xu Y C，Yang C L. The study of weak signal detection arithmetic based on chaotic oscillator. Electrotechnical Application，2008，27 （8）：38～41（in Chinese））

11 谢涛，魏学业.混沌振子在微弱信号检测中的可靠性研究.仪器仪表学报，2008，29（6）：1265～1269（Xie T，Wei X Y. Study on reliability of chaotic oscillator in weak signal detection. Chinese Journal of Scientific Instrument，2008，29（6）：1265～1269（in Chinese））

Received 8 February 2015，revised 6 May 2015.

*The project supported by National Natural Science Foundation of China（51375037），and the Program for New Century Excellent Talents in University（NCET-12-0759）

APPLICATION OF CHAOTIC OSCILLATOR IN FAULT FEATURE EXTRACTION OF ROLLING BEARING*

Li Lingyang Wang Huaqing†Xu Xintao Yang Xiao
（College of Mechanical and Electrical Engineering，Beijing University of Chemical Technology，Beijing 100029，China）

AbstractFault signal of rolling bearing is often weak periodic，and the chaotic oscillator is very sensitive to weak periodic signal with specific frequencycan detect the fault signal effectively. he mathematical model and the basic detection principle of the chaotic oscillator were introduced，the determination method of the dynamic critical threshold. The chaotic oscillator detection method was applied to the fault signal of rolling bearing，including the outer ring，the inner ring and the rolling elementwhether there was a fault signal through the changes between the output phase diagrams the detection of the fault signal rolling bearing was implemented effectively.

Key wordschaotic oscillator， rolling bearing， invariant moment， weak signal， fault feature extraction

DOI：10. 6052/1672-6553-2015-032

通讯作者†E-mail：wanghq_buct@ hotmail. com

Corresponding author†E-mail：wanghq_buct@ hotmail. com