利用弯矩影响线的移动荷载识别方法*

钱长照陈昌萍

（1.厦门理工学院土木工程与建筑学院，厦门 361024）（2.中加噪声与振动控制研究所，厦门 361024）



利用弯矩影响线的移动荷载识别方法*

钱长照1，2†陈昌萍1，2

（1.厦门理工学院土木工程与建筑学院，厦门 361024）（2.中加噪声与振动控制研究所，厦门 361024）

摘要基于模态叠加理论，通过桥梁多个截面处加速度响应数据，计算得到桥梁受移动荷载作用下的模态加速度.根据d′Alembertian原理，桥梁截面任意时刻的动弯矩可看作是任意时刻受惯性分布力和移动荷载作用下的静弯矩.利用影响线，建立起移动荷载与弯矩之间的关系，提出了一种利用弯矩影响线识别移动荷载的方法.算例表明，当荷载只有一个时，可由单点弯矩直接识别，当有多个移动荷载时，可基于多个截面的弯矩数据，利用最小二乘法可以有效的识别出任意时刻作用于桥梁上的移动荷载值.该方法避免了求解桥梁的动力学微分方程，识别精度高且过程简单，适合于工程应用.

关键词荷载识别， 影响线， 移动荷载， 模态叠加原理

2014-09-08收到第1稿，2015-07-16收到修改稿.

*国家自然科学基金资助项目（51108047）、厦门市科技计划项目（3502Z20143028）

引言

随着桥梁轻型化发展，车流量不断增大，车桥相互作用越来越不可忽略.由于车辆通过桥梁时车辆轮轴传递给桥梁的荷载是随位置和时间不断变化的动态荷载，使桥梁产生交变应力，导致路面或桥梁结构的疲劳损伤或破坏［1］.因此越来越受到桥梁运营、维护、桥梁设计及交通运输管理等部门的关注.近年来，国内外学者对桥梁上移动荷载识别理论进行了深入的研究，提出了一系列识别方法. O′Connor and Chan提出了第一识别法（IMI）［2］和第二识别法（IMII）［3］，S. S. Law等提出了时域法（TDM）［4］和频时域法（FTDM）［5］，这些方法奠定了移动荷载识别的理论基础［6］，但这些方法应用到工程中还存在一些问题，如第一识别法（IMI）和第二识别法（IMII）识别精度不高，时域法（TDM）和频时域法（FTDM）识别时间过长且需要大量数据等等.因此，国内外学者不停探索新的识别方法以及算法，模型上也在不断的改进.余岭［7］等对移动荷载识别方程的不适定性进行了研究，提出了改善和解决超定方程组欠秩和病态问题的方法.以上这些方法中所采用数据或为桥梁的加速度响应，或为桥梁挠度响应数据.事实上，P. Asnachinda［8］研究表明采用梁的弯矩数据识别会有更好的效果.但该文仍然采用求解梁的动力学微分方程，建立弯矩响应和荷载的关系，识别过程反而显得复杂.

本文提出的荷载识别方法中，同时采用响应加速度数据和弯矩数据，加速度数据用来分离模态加速度，从而表达出桥梁振动过程中的惯性力.然后基于影响线和达朗贝尔原理，建立起截面弯矩与移动荷载之间的关系，利用截面弯矩数据识别出移动荷载的大小.该方法具有计算精度高，识别速度快，且对数据量的需求不高，适合工程应用.

1 识别方程的推导

对于简支梁桥受移动车辆作用问题，力学模型可以简化为如图1所示的简支梁受一组移动荷载作用.其中梁的模型考虑为均质等截面模型，跨长L，抗弯刚度EI，单位长度质量为m，忽略剪切变形和转动惯量的影响（即采用Euler-Bernoulli理论），则系统的动力学方程和边界条件为

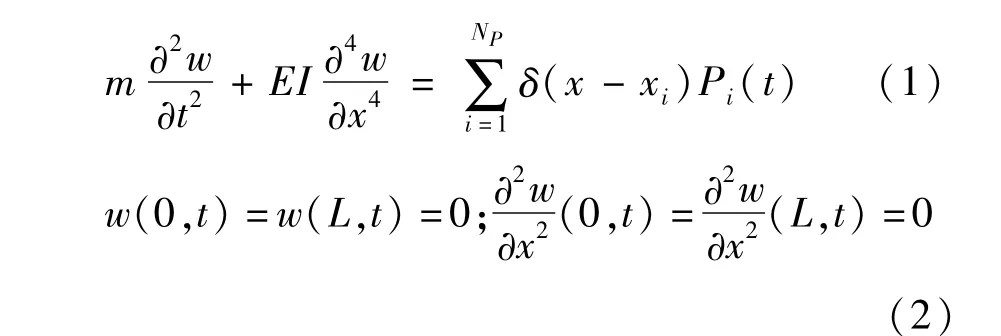
式中，w（x，t）表示x处t时刻梁的挠度，xi是Pi（t）作用位置，δ（x - xi）为Directδ函数，满足

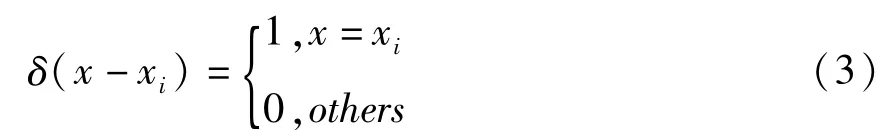
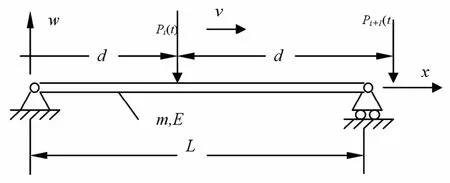
图1 受一组移动荷载作用的简支梁模型Fig. 1 Simplified beam under a set of moving loads

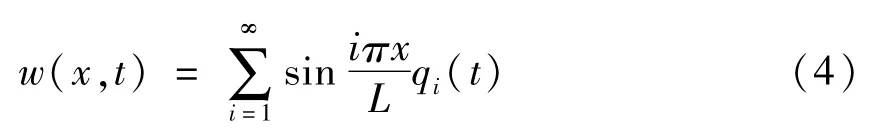
式中qi（t）（i =1，2，3，…）是第i阶模态位移.上式对时间取二阶导数，则可得简支梁任意t时刻x位置处的加速度

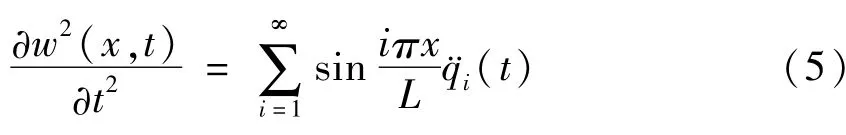
利用Garlerkin截断，可只取N阶模态.则对于某一截面xj处的加速度可以表示为

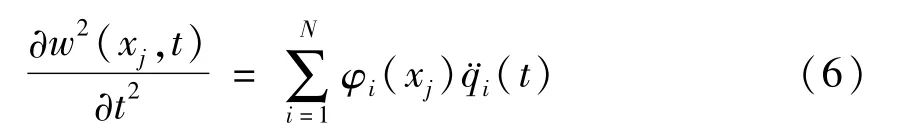
事实上，桥梁上某一截面处的加速度是很容易由试验测得的.如果在桥梁顺桥向布置M个测点测量加速度，则可得到前N阶模态加速度和测点加速度之间的关系，用矩阵表示如下

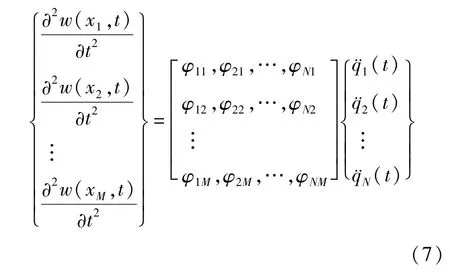
根据d′Alembertian原理，任意时刻桥梁所受的惯性力p（x，t）可表示为

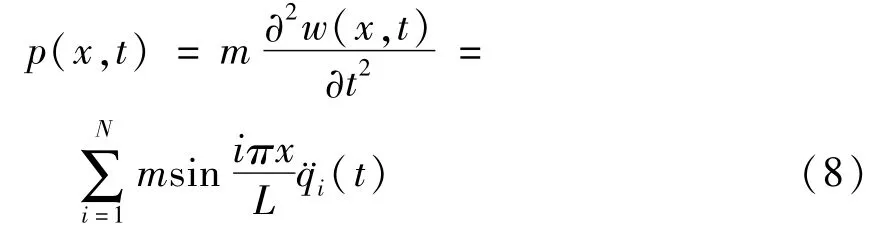
简支梁x = xk截面处的弯矩影响线

式中，a是xk截面距左端支座的距离，b = L - a是xk截面距右端支座的距离.考虑桥梁同时受到车辆和惯性力作用，xk截面处的弯矩可利用影响线计算得到

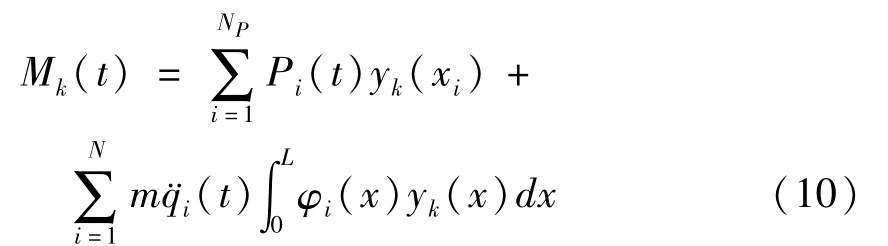
利用梁的弯曲应变与截面弯矩之间的关系，则可根据测得的弯曲应变计算得到截面弯矩随时间变化的函数，惯性分布力也可由影响线与模态函数积分得到，因此上式左侧量为已知，因此任意时刻仅P（t）为未知量.若桥梁上仅一个荷载，则可由上式直接得到.若桥梁同时有多个移动荷载，则上式需重写为

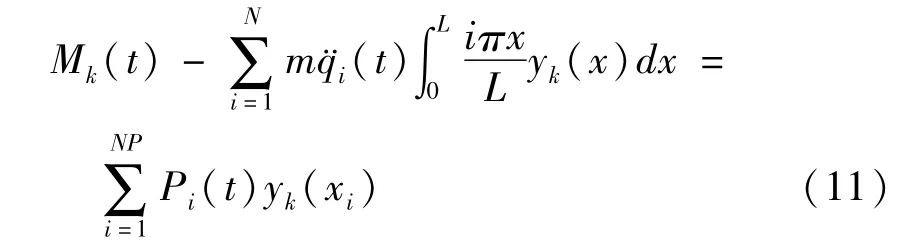
式中NP为t时刻作用在桥梁上的荷载数目xi为第i个荷载作用位置，由于含有NP个位置梁，则需要至少NP个测点的弯矩数据，组成矩阵方程

式中

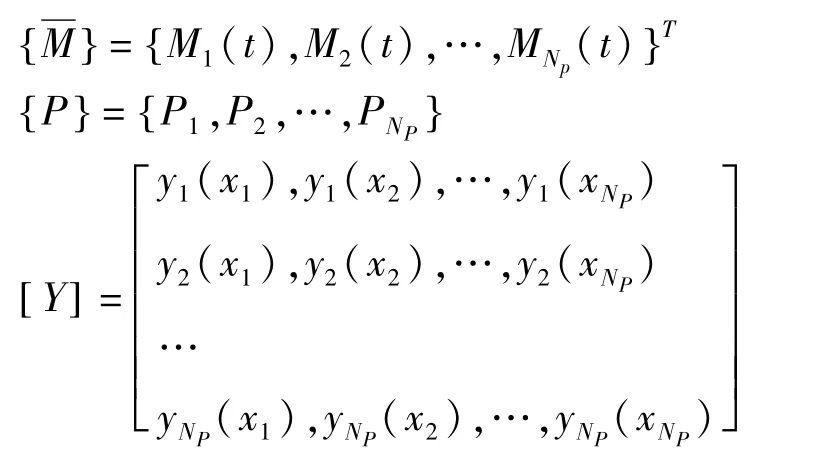
注意到[Y ]是奇异性矩阵，因此需用最小二乘法等方法近似求解，关于最小二乘法的计算过程本文采用MATLAB编程实现，具体过程不再赘述.

2 算例分析

当桥上只有一个移动荷载作用作用时，利用方程（10），则荷载可简单的利用任意一截面处的弯矩数据则得到

当桥上有多个移动荷载作用时，利用方程（9），需要有多个弯矩观测点识别，理论上，当弯矩观测点数目多于桥上荷载数目时，可以由方程（11）识别，但由于矩阵的奇异性，直接计算是不可能的.为了识别出荷载，采用最小二乘法.选取的弯矩观测点也要尽可能的多.

作为算例，ANSYS仿真中移动荷载为随时间变化荷载P1=10*（1 +0. 05sin30πt）kN，P2=15* （1 + 0. 05sin30πt）kN.两荷载距离4m，移动速度10m/ s.为了识别移动荷载，加速度观测点同样选取跨中，L/4和3L/4处，采用三阶模态截断分解模态加速度.弯矩观测点选取L/8，L/4，3L/8，L/2，5L/ 8，3L/4，7L/8等7个截面.识别结果如图2所示.

图2 整个时间域识别的两荷载Fig. 2 Identified loads at all time domain

图3 识别荷载误差Fig. 3 Error of identification results

由图2可以看出，在当有荷载上桥和出桥的时候，识别结果与实际荷载相差较大，其余情况识别结果较为理想.为了比较识别结果与实际荷载的差，定义识别误差

根据（14）式定义的误差计算公式作图如图3所示，为了更清晰的掌握中间段的识别精度，做荷载在［10m，20m］区间段的误差图如图4所示.由图4可以看出，误差在5%左右，这个精度对于荷载识别与其他方法比较也是令人满意的.

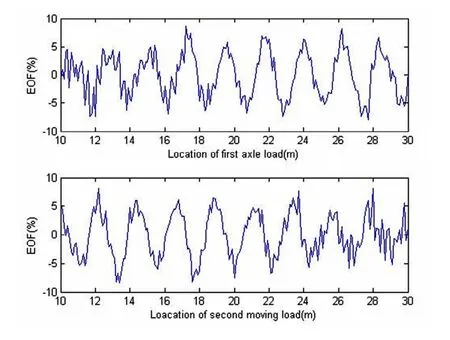
图4 荷载位置在［10，20］范围内的识别误差Fig. 4 Error of identification results in location domain［10，20］

3 结论

本文基于模态叠加原理和d′Alembertian原理，利用弯矩影响线提出了一种识别移动荷载的新方法.该方法创新点在于同时使用了弯矩响应数据和加速度数据，避免了求解移动荷载作用下的动力学方程.通过几个算例，验证了该方法的有效性，并得到一些结论：

（1）通过模态数据可以从实测的加速度数据中得到模态加速度，从而桥梁受到的惯性力可以有效的计算出来；

（2）利用影响线求解荷载识别问题的方法是有效的；

（3）相比其他的方法，该方法可以在已知任意时刻或任意时段弯矩和加速度数据的基础上进行识别，而不需要完全知道移动荷载通过桥梁的整个过程数据；

算例的结果验证了该方法对移动荷载识别有效性和精确性，同时该方法的简洁性更有利用荷载识别在工程中的应用.

参 考 文 献

1 Kozin F，Natke H G. System identification techniques. Structural Safety，1986，3（3-4）：269～316

2 Connor O，Chan T H T. Dynamic wheel loads from bridge strains. Journal of Structural Engineering ASCE，1988，114（8）：1703～1723

3 Chan T H T，Law S S，Yung T H，Yuan X R. An interpretive method for moving force identification. Journal of Sound and Vibration，1999，219（3）：503～524

4 Law S S，Chan T H T，Zeng Q H. Moving force identification：a time domain method. Journal of Sound and Vibration，1997，201（1）：1～22

5 Law S S，Chan T H T，Zeng Q H. Moving force identification：a frequency and time domains analysis. Journal of Dynamic Systems，Measurement and Control ASME，1999，12（3）：394～401

6 Yu L，Chan T H T. Recent research on identification of moving loads on bridges. Journal of Sound and Vibration，2007，305（1-2）：3～21

7 余岭，陈震.桥梁移动荷载识别的不适定性及其实验研究.振动与冲击，2000，19（1）：58～70（Yu L，Chen Z. Experimental study on ill-conditioning problem in identification of moving vehicle loads on bridge. Journal of Vibration and Shock，2000，19（1）：58～70（in Chinese）

8 Asnachinda P，et al. Multiple vehicle axle load identification from continuous bridge bending moment response. Engineering Structures，2008，30（10）：2800～2817

9 Qian C Z，Chen C P，Hong L，Dai L M. Axle load identification of moving vehicles based on influence lines of bridge bending moment. Nonlinear Engineering，2014，3 （3）：125～131

10 Qian C Z，Chen C P，Xiao Y G. Identification method for moving loads over continuous beam based on bending moment influence lines. Applied Mechanics and Materials，2014，638-640：1079～1084

Received 08 September 2014，revised 16 July 2015.

*The project supported by National Natural Science Foundation of China（51108047），Supported by Science and Technology Planning Project of Xiamen（3502Z20143028）

METHOD FOR MOVING FORCE IDENTIFICATION USING BENDING MOMENT INFLUENCE LINE*

Qian Changzhao1，2†Chen Changping1，2
（1. Xiamen University of Technology，Xianmen 361024，China）（2. Sino-Canada Research Center for Noise and Vibration Control，Xianmen 361024，China）

AbstractBased on the modal superposition theory，the second order derivative of the modal coordination is firstly obtained from the acceleration of the bridge at several sections. The inertia force of the bridge is then expressed as distributed load by means of the d′Alembertian theory. Using the bending moment influence line of the bridge，the relationships between the moving load and the moment is proposed. The moving force can be obtained at any time points through the developed formula. Case studies show that this proposed method performs high accuracy in identifying time-varying as well as constant moving force. Moreover，this method doesn′t need to deal with the ill-condition due to matrix singularity，which makes it in high efficiency and appropriate for engineering application.

Key wordsload identification， influence line， moving force， modal superposition theory

DOI：10. 6052/1672-6553-2015-061

通讯作者†E-mail：qiancz@163. com

Corresponding author†E-mail：qiancz@163. com