有限元法的轴向运动梁的激励功率谱辨识*

刘涛罗梦翔吴炜史济涛蔡国平†

（1.上海交通大学工程力学系，海洋工程国家重点实验室，上海 200240）（2.中国空空导弹研究院，洛阳 471009）



有限元法的轴向运动梁的激励功率谱辨识*

刘涛1罗梦翔1吴炜2史济涛2蔡国平1†

（1.上海交通大学工程力学系，海洋工程国家重点实验室，上海 200240）（2.中国空空导弹研究院，洛阳 471009）

摘要主要考虑弯曲变形的细长轴向运动梁，可以作为工程中广泛应用在航天器天线、液体输送管道、汽车驱动带、电梯缆索等的简化机构.对轴向运动柔性梁线性微分方程，采用复模态分析方法导出两端简支和固支边界条件下的固有频率方程；采用Ritz法建立轴向运动梁的有限单元法模型.基于该模型在多种边界条件下进行梁的横向振动分析，并开展定点激励下激励功率谱的辨识.仿真结果表明，与传统的Galerkin截断方法相比.有限元方法能够克服分析方法的建模困难，对复杂边界梁进行有效的分析，对激励的功率谱能够有效地辨识.

关键词轴向运动梁， 复模态， 有限元， 复杂边界， 功率谱辨识

2014-09-26收到第1稿，2014-12-20收到修改稿.

*国家自然科学基金资助项目（11132001，11272202）、航空科学基金（20120157002）和上海市教委科研重点项目（14ZZ021）资助

引言

工程中存在着大量细长运动结构，例如：航天器天线、液体输送管道、汽车驱动带、电梯缆索等，主要考虑弯曲变形时此类结构可简化为轴向运动梁.当受到外部载荷激励时，结构的横向振动会产生负面效应.对于航空航天结构，外部载荷功率谱辨识的研究有利于地面振动台试验的激励设计.因此，研究轴向运动梁的横向振动和功率谱的辨识问题有着实际工程的应用背景和理论意义.

1965年，Mote［1］在对带锯的研究中，推导出轴向运动梁的横向振动微分方程，并采用Galerkin截断法得出了简支梁的前三阶固有频率和模态振型. 1990年，Wickert［2］和Mote提出复模态分析法开展对轴向运动梁的进行研究，并得出简支和固支边界轴向运动梁的固有频率与模态函数；Öz［3］通过线性梁的假定求出了固支边界下进行了固有频率计算及稳定性分析. 1994年，Stylianou［4，5］则建立伸展机构的轴向运动梁的有限元模型，分析了响应及稳定性问题.近年来，国内学者也积极开展了轴向运动梁稳定性、非线性及受迫振动等问题的研究. 2006年，陈立群等［6］研究了粘弹性轴向运动梁在混合边界条件下的振动与稳定性问题；2007年，张哲荣［7］等利用有限元模型分析了Rayleigh梁的横向振动稳定性问题. 2008年，李德双等［8］研究了轴向运动带的横向与纵向运动的耦合振动问题. 2010年，黄建亮［9］等采用增量谐波平衡法研究了轴向运动梁在纵向与横向振动耦合下的自由振动响应. 2011年，王亮等［10］研究了高速轴向运动梁的模态及频率特征；同年，李彪等［11］研究了两端自由的轴向运动Timoshenko梁的横向振动问题. 2013年，丁虎［12］等对轴向运动梁的横向振动问题非线性问题进行了综述分析.

上述文献中对于梁的分析多针对两端简支和两端固支条件这两种边界条件，而对于复杂条件下的轴向运动梁较少涉及；对于轴向运动梁的激励功率谱辨识方面的研究也较少.本文依据Hamilton原理建立轴向运动柔性梁的运动微分方程，导出了两端简支梁和两端固支梁边界下的系统固有频率方程，采用Ritz法对微元运动微分方程进行离散化，建立了有限元法的单元运动方程，并基于此模型开展了定点随机激励下的功率谱辨识的研究.应当说明的是，我们前期已经开展了基于Ritz法离散的轴向运动梁的功率谱辨识研究，并取得了较好的结果，详细内容可以参考文献［13］.

1 动力学方程

1. 1 运动微分方程

考虑等截面轴向运动柔性梁的横向弯曲振动，如图1所示.假定柔性梁有恒定轴向运动速度υ，轴向有恒定张力P，横向作用有分布式外部载荷f （x，t），等截面面积为A，截面的惯性矩为I，弹性模量为E，密度为ρ，长度l.则在x方向的应变εxx为

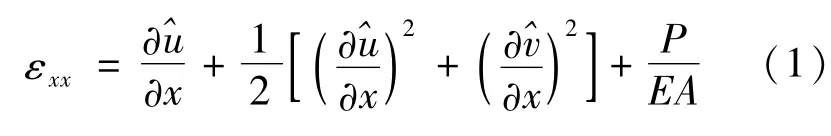
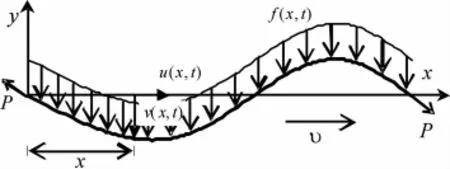
图1 轴向运动梁模型Fig. 1 Model of an axially moving beam

在截面A及长度［0，l］区间内进行积分，由此得出梁的总势能与总动能分别为

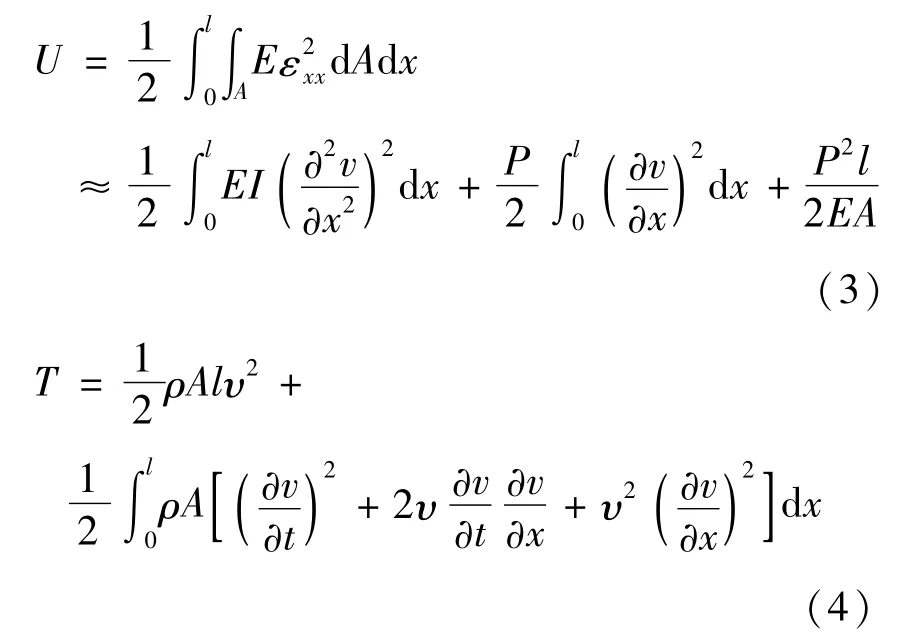
外力f（x，t）所做虚功为

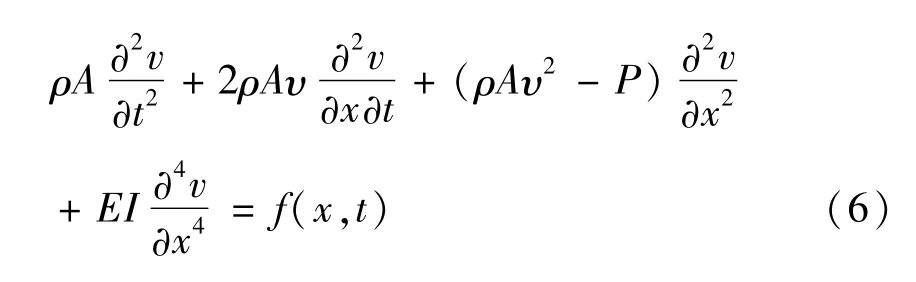
式（6）即为轴线运动梁的线性运动微分方程.

1. 2 固有频率分析

对于两端简支和两端固支简单边界，可以采用复模态分析法［14，15］对系统固有频率进行分析.令v （x，t）=φ（x）ejωt+¯φ（x）e- jωt（j为虚数单位），代入式（6）中，并令f（x，t）=0，则有

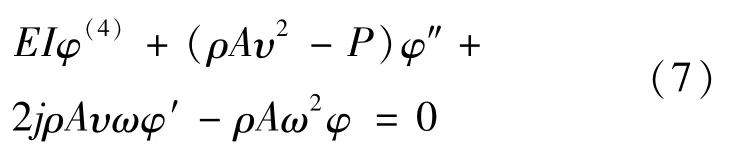
令关于φ的特征根方程的解为jβ，代入式（7）可得

设式（8）有解βi（i = 1～4），由此导出复模态振型为考虑梁具有不同简单的边界条件

由于振型函数φ（x）不恒为零，则通过式（9）得到关于系数Ci齐次线性方程组系数矩阵的行列式为零.则有

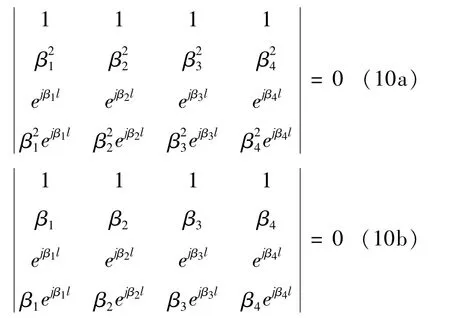
式（10a）与式（10b）分别对应两端简支与固支边界条件的行列式系数方程.由式（8）和式（10）组成关于ω、βi（i =1～4）的非线性方程组，即可得出梁的固有振动频率.应当说明的是，在轴向运动梁的横向振动问题的分析中，随着轴向速度的增大或轴向压力的增大，梁的固有频率会随之减小.当第一阶固有频率为零时，其所对应的轴向运动速度称为临界速度，超过临界速度之后梁的运动将变得不稳定［16］.

在实际应用中，复模态分析法计算响应存在困难；针对简单边界条件，可以采用Galerkin法对轴向运动梁的运动微分方程进行离散化，令

其中，φi（x）为对应边界条件的无轴向速度梁的振型函数，n为Galerkin法计算阶数.将式（11）代入微分方程式（6）中，并左乘ΦT，在［0，l］区间积分可得

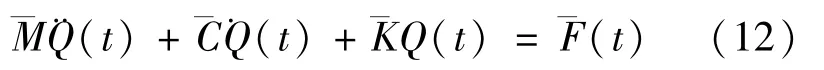
其中，质量阵、阻尼力阵、刚度阵和外力阵分别为

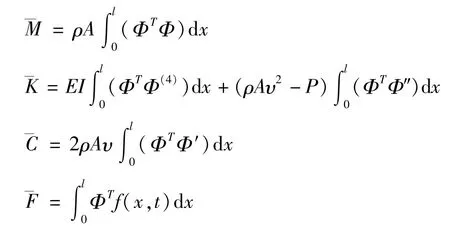
1. 3 有限元模型创建

以下采用Ritz法建立轴向运动梁的有限元模型.设单元的长度为Δl，单元左右节点i与j的横向位移与转角分别为vi、φj、vi、φj.

图2 有限单元划分示意图Fig. 2 Schematic representation of beam element model

将有限单元的形函数gk（x）设为［4］

由此得到单元长度Δl内的内插函数ve（x，t）

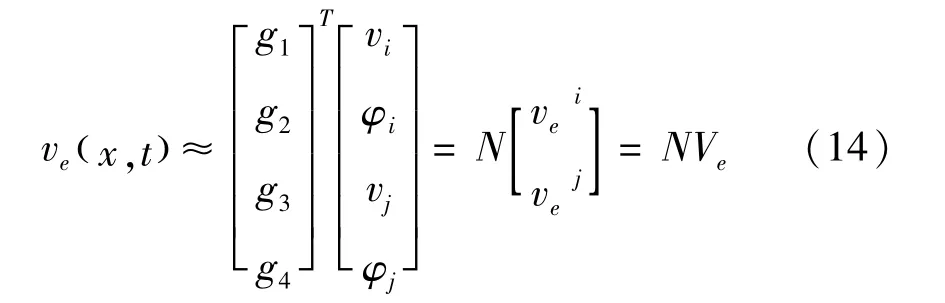
当不考虑附加质量m和刚度k时，将ve（x，t）的内插函数代入势能式（3）、动能式（4）和虚功式（5）中；由Lagrange方程得到单元的运动微分方程

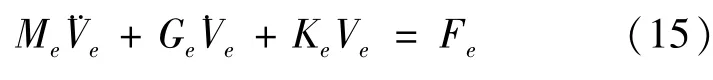
其中，单元的质量阵、陀螺力阵、刚度阵和外力阵分别为

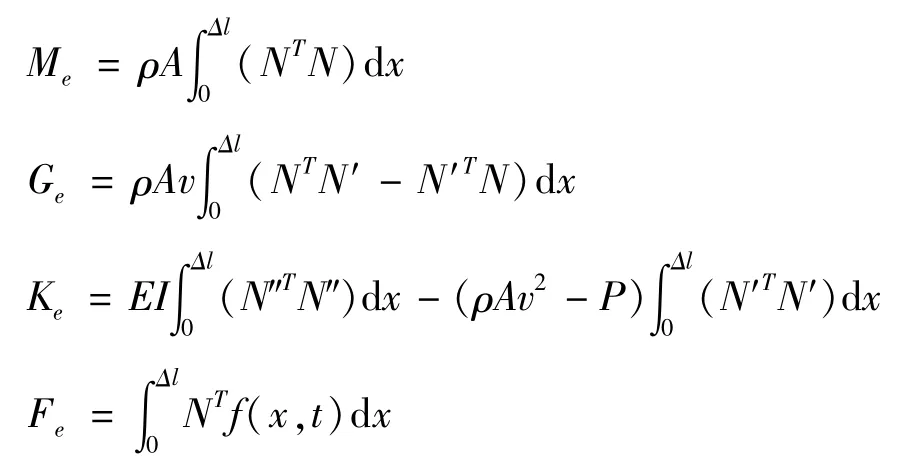
考虑附加质量m和刚度k后，对应节点处的单元矩阵需要做出对应改变.如图2所示，i节点质量阵施加附加质量m，j节点刚度阵施加附加刚度k.将单元矩阵进行组集与施加附加边界条件，可得系统的运动方程其中，总质量阵M为对称正定阵，总陀螺力项G为对称正定阵，因此系统的运动将具有陀螺系统［17，18］的特征.

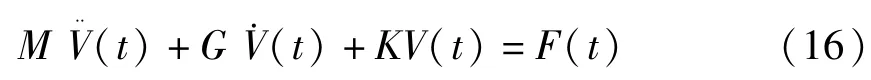
相较Galerkin方法，有限元法克服了寻找形函数的困难，并且能够适应较为复杂的模型建模，因此可以应用到更加复杂模型中进行建模.

2 响应计算与功率谱辨识

2. 1 有限元模型的响应

由于式（16）中陀螺力项G的存在，振动分析需采用复模态法.将式（16）改写为状态方程形式［17］

其中，φR、φI为各阶实模态和虚模态向量，且满足

ii 表1的正则化正交关系

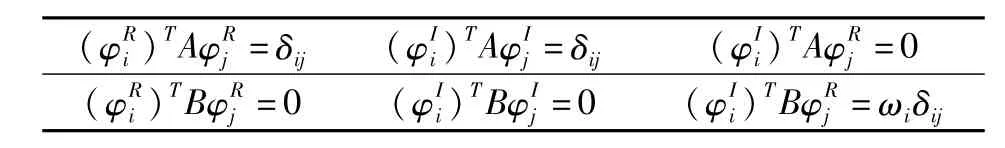
表1 模态的正则化正交关系Table 1 Normality and orthogonality relations of modes

其中，ωi为第i阶固有振动频率

利用正交性条件，对式（18）进行变换，有

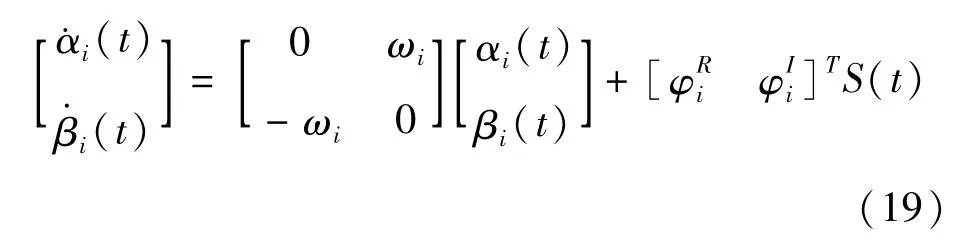
由式（15）可以解得外力作用下的各单元的外力阵，组集后可得S（t）；则Q（t）的响应值为Y（t）的下半部分，且考虑到单元形式的插值函数式（14），由此得出梁上任意一点在外力作用下的响应

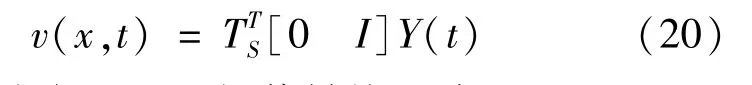
其中，TS为响应v（x，t）插值转换矩阵.

2. 2 有限元模型的功率谱辨识

考虑如下情况的响应，在定点xf处施加随机外力f（t），即令f（x，t）= f（t）δ（x - xf），其中δ（·）为Dirac函数.将f（x，t）代入式（19）可得

其中，TF为外力f（x，t）的插值转换矩阵.

考虑梁初始处于静平衡状态，将式（21）代入式（18），并两端同时取傅里叶变换可得

考虑点xs处横向振动响应v（xs，t）的自相关函数RS（t），由式（20）可得

由Wiener - Khinchin定理［19］，对响应的自相关函数RS（t）取傅里叶变换可得对应的功率谱密度函数

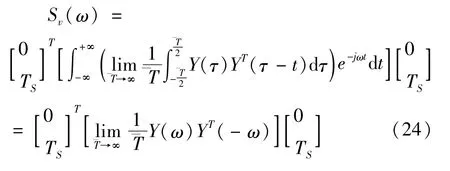
将式（22）代入式（24），可得

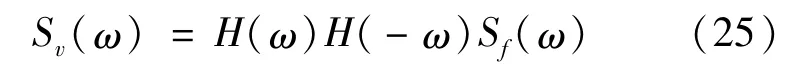
由式（25）易得

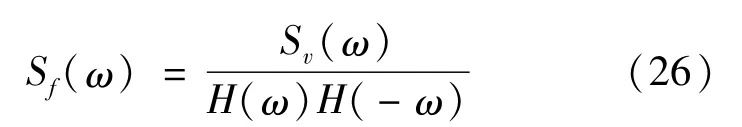
式（26）即为定点激励的功率谱辨识公式.

3 数值仿真

本节进行数值仿真以验证文中所给有限元方法的有效性.分别考虑两端固支和复杂边界条件下的轴向运动梁的横向振动问题.

首先考虑两端固支梁边界条件下的轴向运动梁的功率谱辨识，参考文献［15］设定如下参数：等截面均质钢材，长度l =2m，圆截面半径R =0. 05m，密度ρ=7850kg/ m3，弹性模量E =196GPa.考虑在梁上一定点施加集中力，梁的轴向运动速率为v =10m/ s，梁的轴向压力P = -10kN（负值表示处于轴向受压状态）.对其进行静力屈曲校核，9495kN，远未达到屈曲；参考文献［16］可得，在线性条件下的临界速度；因此，设定的条件下轴向运动梁的运动稳定.

考虑梁横向振动初始处于静止平衡位置，梁上xf=0. 4m处一定点施加集中力f（t），得出点xs= 1. 8m处响应，由此进行功率谱的辨识，Galerkin截断数值方法截断阶数n取为10.在xf处施加集中载荷f（t）=［13sin（7t）+ 11sin（19t）+ rand（t）］（N），其中rand（t）为取样时间内的随机激励，其方差为2.通过复模态分析法进行迭代求解得出的前三阶固有频率分别为111. 09Hz、306. 42Hz、600. 82Hz，通过Galerkin法与有限元方法计算得到的前三阶固有频率的与迭代解的相对误差在10-6以内；说明Galerkin法与有限元法的分析是有效的.图3为采用有限元模型进行响应与功率谱辨识的数值仿真结果，其中（a）为xs处的频响曲线；（b）为施加的激励的功率谱与辨识功率谱.由图中结果可以看出，本文的方法能够有效地进行定点随机外载荷的功率谱辨识.

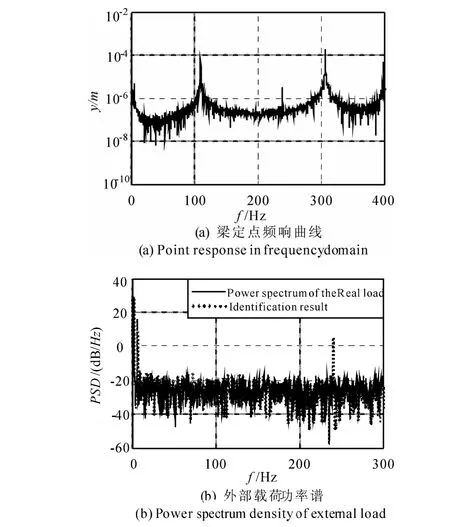
图3 两端固支梁的定点频响曲线与载荷功率谱辨识结果Fig. 3 Point response in frequency domain and PSD identification of the clamped axially moving beam

然后考虑复杂边界条件下的轴向运动梁的功率谱辨识，由于边界条件的复杂性，采用Galerkin方法很难找到一组适合的形函数，而有限元方法则能够较为容易的克服该困难.如图4所示，设定复杂条件下的轴向运动梁有如下参数：等截面均质钢材料，密度ρ= 7850kg/ m3，弹性模量E = 196GPa，长度l =2. 4m，横截面积A =0. 015m2，截面惯性矩I =1. 25×10-5m4.梁的轴向运动速率为v =15m/ s，轴向力P =0N.在l1=0. 4m与l3=1. 8m处施加简直边界；在l2=1. 4m处有集中质量m =60kg；在梁的两端分别施加有线弹簧，劲度系数分别为k1= 3. 5×104N/ m，k2=4. 5×104N/ m.

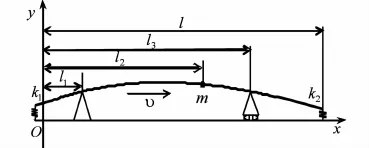
图4 复杂边界条件下的轴向运动梁Fig. 4 Model of an axially moving beam under complex boundaries

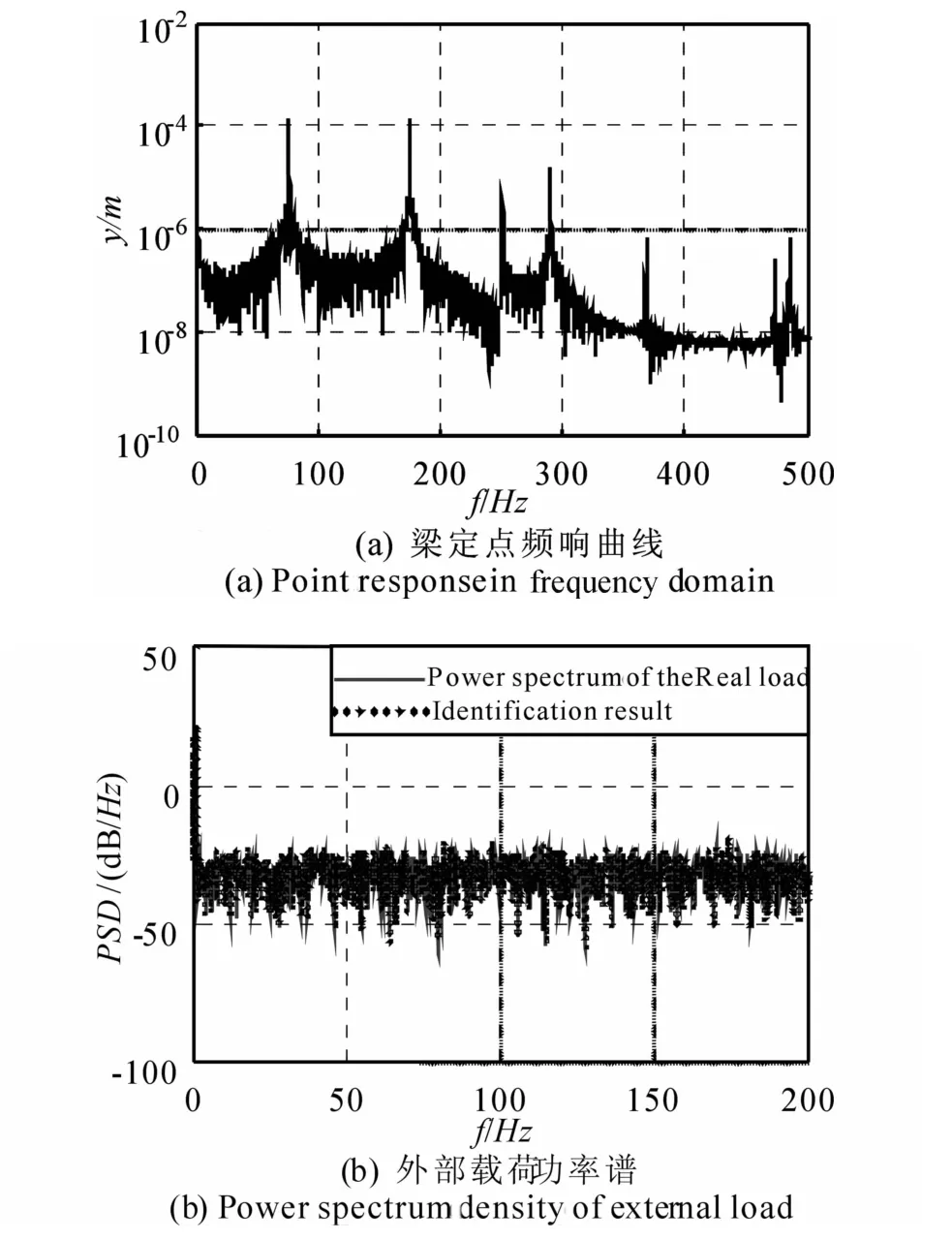
图5 复杂条件的定点频响曲线与载荷功率谱辨识结果Fig. 5 Point response in frequency domain and PSD identification of the axially moving beam under complex boundaries

考虑在梁上xf=0. 48m处施加集中力f（t），得出点xs=2. 16m处响应，考虑初始处于静止平衡位置.在xf处施加集中载荷f（t）=［13sin（7t）+11sin （19t）+ rand（t）］（N），其中rand（t）为取样时间内的随机激励，其方差为1.由有限元法计算得到系统的前三阶固有频率分别为75. 58Hz、174. 78Hz、291. 12Hz.由于边界条件复杂，不能直接计算出临界速度，但由前面的计算可知，固有频率大于零，因此在此条件下的轴向运动稳定.图5为有限元方法数值仿真的结果，其中（a）为xs处的频响曲线；（b）为施加的激励的功率谱与辨识功率谱.由图中结果可以看出，本文的方法能够有效地进行定点随机外载荷的功率谱辨识.

4 结束语

本文以轴向运动梁为研究对象，采用复模态分析方法建立了两端简支和固支梁的固有频率方程，采用Ritz法建立梁的运动有限元分析模型，并基于此导出了定点载荷的功率谱辨识方法.仿真结果表明，通过有限元方法能够有效地克服传统分析方法中形函数选取的困难，本文的方法能够有效地对定点随机外载荷进行功率谱辨识.

参 考 文 献

1 Mote Jr C D. A study of band saw vibrations. Journal of the Franklin Institute，1965，276（6）：430～444

2 Wicker J A，Mote Jr C D. Classical vibration analysis of axially moving continua. Journal of Applied Mechanics，1990，57（3）：738～744

3 Öz H R. On the vibrations of an axially traveling beam on fixed supports with variable velocity. Journal of Sound Vibration，2001，239（3）：556～564

4 Stylianou M，Tabarrok B. Finite element analysis of an axially moving beam，part I：time integration. Journal of Sound and Vibration，1994，178（4）：433～453

5 Stylianou M，Tabarrok B. Finite element analysis of an axially moving beam，part II：stability analysis. Journal of Sound and Vibration，1994，178（4）：455～481

6 Chen L Q，Yang X D. Vibration and stability of an axially moving viscoelastic beam with hybrid supports. European Journal of Mechanics A/ Solids，2006，25（6）：996～1008

7 Chang J R，Lin W J，Choi S T. Vibration and stability of an axially moving rayleigh beam over a stationary support with telescopic motion. In：24th National Conference on Mechanical Engineering of CSME. Taipei：Chinese Society of Mechanical Engineers，2007：CSME1648～1653

8 李德双，戈新生.轴向运动带的横向与纵向振动分析.北京机械工业学院学报，2008，23（1）：18～22（Li D S，Ge X S. Analyses of an axially moving belt with transverse and longitudinal vibrations. Journal of Beijing Institute of Machinery，2008，23（1）：18～22（in Chinese））

9 黄建亮，陈树辉.纵横向耦合轴向运动梁的自由振动响应研究.动力学与控制学报，2010，8（4）：316～321 （Huang J L，Chen S H. Study on vibration of an axially moving bean with coupled transverse and longitudinal motions. Journal of Dynamic and Control，2010，8（4）：316 ～321（in Chinese））

10 Wang L，Chen H H，He X D. Modal frequency characteristics of axially moving beam with supersonic/ hypersonic speed. Transactions of Nanjing University of Aeronautics & Astronautics，2011，28（2）：163～168

11 Li B，Tang Y Q，Chen L Q. Nonlinear free transverse vibrations of axially moving Timoshenko beams with two free ends. Science China Technological Sciences，2011，54 （8）：1966～1976

12 丁虎，陈立群，张国策.轴向运动梁横向非线性振动模型研究进展.动力学与控制学报，2013，11（1）：20～30（Ding H，Chen L Q，Zhang G C. Advances in nonlinear models for transverse vibration of axially moving beams. Journal of Dynamic and Control，2013，11（1）：20～30（in Chinese））

13 刘涛，吴炜，史济涛等.轴向运动梁的激励功率谱辨识.航空兵器，2014，4：45～48（Liu T，Wu W，Shi J T，etc. Identification of excitation power spectrum denstity of an axially moving beam. Aero Weaponry，2014，4：45～48（in Chinese））

14 李彪，丁虎，陈立群.两端受套筒约束轴向运动梁的横向振动固有频率和模态函数.振动与冲击，2010，29 （9）：55～57（Li B，Ding H，Chen L Q. Natural frequencies and modal functions of transverse vibration of axially moving beam constrained by rotating sleeves with rotational springs. Journal of Vibration and Shock，2010，29（9）：55～57.（in Chinese））

15 马国亮，陈立群.高速运动梁的临界速度、固有频率和模态函数.力学季刊，2013，34（4）：541～545（Ma G L，Chen L Q. Critical velocity，frequency，and modal functions of beam moving with high speed. Chinese Quarterly of Mechanics，2013，34（4）：541～545（in Chinese））

16 张国策，丁虎，陈立群.两端固定超临界轴向运动梁横向平衡位形与振动.振动工程学报，2011，24（1）：8～13（Zhang G C，Ding H，Chen L Q. Transverse equilibrium and vibration of axially moving beams with fixed boundaries in the supercritical regime. Journal of Vibration Engineering，2011，24（1）：8～13（in Chinese））

17 Meirovitch L. A modal analysis for the response of linear gyroscopic systems. Journal of Applied Mechanics，1975，42（2）：446～450.

18 钟万勰.应用力学对偶体系.北京：科学出版社，2002：101～106（Zhong W X. Duality system in applied mechanics. Beijing：Science Press，2002：101～106（in Chinese））

19 吴大正，杨林耀，张永瑞等.信号与线性系统分析（第4版）.北京：高等教育出版社，2005：162～166（Wu D Z，Yang L Y，Zhang Y R，et al. Signal and linear system analysis. Beijing：Higher Education Press（4thEdition）2005：162～166（in Chinese））

identification of power spectrum density

Received 26 September 2014，revised 20 December 2014.

* The project supported by National Natural Science Foundation of China（11132001，11272202），Aeronautical Science Foundation of China （20120157002），Innovation Program of Shanghai Municipal Education Commission（14ZZ021）

IDENTIFICATION OF EXCITATION POWER SPECTRUM DENSITY FOR AN AXIALLY MOVING BEAM USING FINITE ELEMENT METHOD*

Liu Tao1Luo Mengxiang1Wu Wei2Shi Jitao2Cai Guoping1†

（1. Department of Engineering Mechanics，State Key Laboratory of Ocean Engineering，Shanghai Jiaotong University，Shanghai 200240，China）（2. China Airborne Missile Academy，Luoyang 471009，China）

AbstractMany mechanical devices，such as spacecraft antennas，pipes conveying fluid and elevator cable，can be simplified as axially moving slender beams，since their main elastic deformation is taken as transverse bending. Based on the complex model analysis procedure，the formula of natural frequency for the simple - supported and fixed beams are firstly derived from the linear differential equations in this paper. Moreover，in terms of Ritz method，a finite element model of axially moving beams is constructed. The system response under external excitation and the transforming relationship of power spectrum density（PSD）between external excitation and system response in frequency domain are obtained. To this end，the PSD of external excitation through the transforming relationship is finally indentified. Importantly，it is shown from the comparison between the proposed FE model and the traditional Galerkin truncation method that the finite element method can solve the modeling problem of the analysis method，and it is more effective in identifying the PSD of external excitation for the axially moving beams with complex boundaries.

Key wordsaxially moving beam， complex modal analysis， finite element method， complex boundaries，

DOI：10. 6052/1672-6553-2015-014

通讯作者†E-mail：caigp@ sjtu. edu. cn

Corresponding author†E-mail：caigp@ sjtu. edu. cn