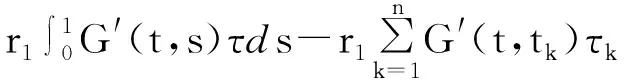Banach空间中一类二阶脉冲积分微分方程多点边值问题*

饶显波,韦煜明

(广西师范大学 数学与统计学院，广西 桂林 541004)

Banach空间中一类二阶脉冲积分微分方程多点边值问题*

饶显波,韦煜明

(广西师范大学 数学与统计学院，广西 桂林 541004)

研究Banach空间中二阶脉冲积分微分方程多点边值问题正解的存在性.在给定的条件下，运用锥拉伸与锥压缩不动点定理得出边值问题正解存在性的充分条件.

脉冲微分方程;边值问题;正解;不动点定理

0 引言

脉冲微分方程是研究一个过程突然发生变化的基本工具,能够充分体现瞬时突变现象对系统的影响,能更加真实的地描述自然界状态，脉冲系统在现代科学领域中是广泛存在的，它的理论在经济学、社会科学、生物学、物理学、工程学等有着广泛的运用,因此，对脉冲微分方程的研究已引起了国内外同行的广泛关注.近十年来，对脉冲微分方程一点、两点、多点边值问题的研究已经非常多,并且有大量的成果,[1-5]与此同时，脉冲积分微分方程作为一个重要的分支也得到了人们的关注，[6-9]然而，这些文章中很少有讨论带有一阶导数的二阶脉冲积分微分方程多点边值问题，因此，受上述文献的启发，笔者运用锥压缩与锥拉伸不动点定理证明了一类带有一阶导数的二阶脉冲积分微分方程多点边值问题正解的存在性.

文中，我们讨论了如下的一类二阶脉冲积分微分方程多点边值问题正解的存在性：

(1)

其中f∈C(J×P×P×P×P,P)，P是E中的一个锥，J=[0,1]，Ik∈C[P,P]

0<ε1<ε2<…<ε3<…<εm-2<1.εi≠tk(i=1,2,…,m-2,k=1,2,…,n),

θ为E中的零元素，

其中g∈C[D,R+]，h∈C[D,R+],D={(t,s)∈J×J:t≥s},R+是正实数集，

A0=max‖(Ax)(t)‖，B0=max‖(Bx)(t)‖

其中x(τ+)和x(τ-)分别叫作x(t)在t=tk处的右极限和左极限，

PC[J,P]={x∈PC[J,E]:x(t)≥0} 和PC1[J,P]={x∈PC1[J,E]:x(t)≥0,x′(t)≥0}

显然PC[J,P]是PC[J,E]中的一个锥，PC1[J,P]是PC1[J,E]中的一个锥.

PC1[J,E]在‖x‖1=max{‖x‖pc,‖x′‖pc}下构成一个Banach空间.

J′=J/{t1,t2,…,tk,…,tn}，x∈PC1[J,E]∩C2[J′,E]叫作边值问题(1)的正解当且仅当x(t)≥0,x′(t)≥0，x(t)满足方程(1)

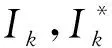
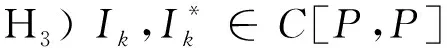
问题(1)是一类带二阶脉冲积分微分方程多点边值问题,本文运用锥拉伸与锥压缩不动点定理讨论了问题(1)存在正解的充分条件,获得了正解存在性的结果,在某种程度上改进和推广了前人的结果.

1 预备知识

在本节中，首先给出一些前提和主要引理.

定理1[7]若E为实Banach空间,P为E中的非空闭凸集，满足

1)au+bv∈P,u,v∈P.且a≥0,b≥0.

2)u,-u∈P,则u=θ.(θ为E中的零元)

则称P为E中的一个锥.

对给定的E中的一个锥P,可在E中引入半序：对任意的x,y∈E,x≤y当且仅当y-x∈P.

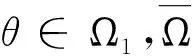
1)Tx≥x,∀x∈P∩∂Ω1,且Tx/≤x,∀x∈P∩∂Ω2,

2)Tx/≤x,∀x∈P∩∂Ω1,且Tx≥x,∀x∈P∩∂Ω2,

引理1 假设条件H1)～H2)全部成立，x∈PC1[J,E]∩C2(J′,E)叫作边值问题(1)的解当且仅当x∈PC1[J,E]是下面脉冲积分方程的解.

(2)

证明：设x是边值问题(1)的解，对(1)式两端积分很容易得到，

(3)

对(3)式积分，有

(4)

令t=1和t=εi，i=1,2,…,m-2，带入(3)式中，可以得到

(5)

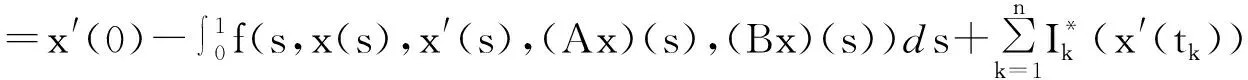
化简得

(6)

将(6)式带入(4)式中可以得到

反之，假设x∈PC1[J,E]是边值问题(2)的解.显然

x(0)=0,△x|t=tk=Ik(x(tk)),k=1,2,…,n

对(2)式微分可得，当t≠tk时，

再次微分上式，得到

x″(t)=-f(s,x(s),x′(s),(Ax)(s),(Bx)(s))

很容易可以得出

故，x∈PC1[J,E]∩C2[J′,E]

因此，引理1得证.

引理2 假设条件(H1～H3)都满足，则边值问题(1)的解x(t)满足x(t)≥0,x′(t)≥0,t∈[0,1].

证明：根据引理1可以得出，

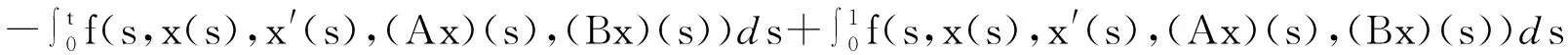
因此引理2 得证.

引理3[3]假设(H1～H3)成立，边值问题(1)有如下Green′的函数：

根据上面的Green′很容易可以得出，G(t,s)满足如下式子，

定义算子T：PC1[J,P]→PC1[J,P]:

由引理1和引理3可以得出：x∈Eθ是算子T的不动点，那么x是边值问题(1)的一个正解.

假设条件(H1～H3)全部成立，由引理2和引理3显然可以得出算子T

T(PC1[J,P])⊂PC1[J,P]，

由积分的绝对连续性和Arzela-Ascoli定理可以得到算子T是一个全连续算子.

2 主要结果

在本段中，将运用定理2证明边值问题(1)正解的存在性.

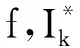
则边值问题(1)至少有一个正解x*(t)∈PC1[J,P]∩C2[J′,E].

证明： 假设H4)成立，则存在一个l>0，使得

和‖f(t,u1,u2,u3,u4)‖≤M，∀t∈J,ui∈P,‖ui‖≤l,i=1,2,3,4,都成立.

其中M=sup{‖f(t,u1,u2,u3,u4)‖,t∈J,ui∈P,‖ui‖≤l,i=1,2,3,4},

另一方面，假设条件H5)成立；则存在一个l1>0，使得

并且ε>0,εk>0，k=1,2,3,…,n,R>r0,t∈J,使得

其中r0=max{l,l1,A0,B0}，

接下来证明：Tx≥ x,x∈P,‖x‖=R>r0.

(7)

事实上，如果存在一个x1∈P,‖x1‖=R>r0，使得Tx1≥x1，则有

0≤x1(t)

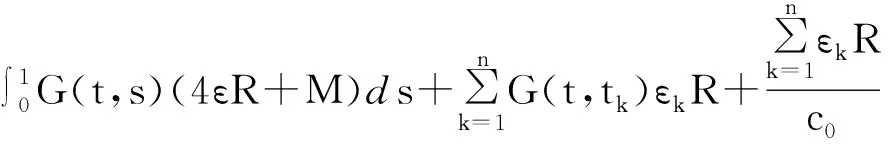
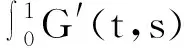
因此，得到‖x1‖<‖x1‖，这显然是矛盾的，故(7)式成立.

紧接着证明:存在0

(8)

事实上，如果存在x2∈P,‖x2‖=r1，使得Tx2≤x2，由条件H6)有，

因此得出，‖x2‖>‖x2‖，这显然是矛盾的，故(8)式成立.

因此，由定理2，T至少有一个不动点x*∈Pr1,R，Pr1,R={x|r1≤x≤R},再由引理1有边值问题(1)至少有一个正解.

故定理3得证.

[1] Liu B, Yu J S. Existence of solution for m-point boundary value problem of second-order impulsive differential equations[J].Apple Math.comput,2002,125(2-3):155-175.

[2] Zhao Y L, Chen H B. Existence of multiple positive solutions for m-point boundary value problems in Banach spaces[J].Apple Math.comput,2008,215(1):79-90.

[3] Jiang W H, Guo Y P. Multiple positive solutions for second-order m-point boundary value problems[J].Math.Anal.appl. ，2007 (327)：415-424.

[4] Feng M Q, Xie D X. Multiple positive solutions of multi-point boundary value problem for second-order impulsive differential equations[J].Apple Math.，2009 (223)：438-448.

[5] Feng M Q, Ge W G. Positive solutions for a class of m-point singular boundary value problems[J].Math.comput.Modeling ，2007 (46)：375-383.

[6] Feng M Q,Pang H H. A class of three-point boundary-value problems for second-order impulsive integro-differential equations in Banach spaces[J].Nonlinear. Ana.，2009 (70)：64-82.

[7] Zhang X M, Feng M Q, Ge W G. Existence of solutions of boundary value problems with integral boundary conditions for second-order impulsive integro-differential equations in Banach spaces[J].Apple Math.comput, 2010 (233)：1915-1926.

[8] Guo D J. Positive solutions of an infinite boundary value problem for nth-order nonlinear impulsive singular integro-differential equations in Banach spaces[J].Nonlinea Ana.，2009 (70)： 2078-2090.

[9] Guo D J.Lakshmikantham V.Nonlinear Problems in Abstract Cones[M].NewYork:Academic Press,1988.

[10]葛渭高.非线性常微分方程边值问题[M].北京：科学出版社，2007：63-64.

[责任编辑 苏 琴] [责任校对 黄招扬]

A Class of Multi-point Boundary-value Problems for Second-order Impulsive Integro-differential Equations in Banach Spaces

RAO Xian-bo，WEI Yu-ming

(SchoolofMathematicalScience,GuangxiNormalUniversity,Guilin541004,China)

This paper investigates the existence of solutions for a class of multi-point boundary-value problems for second-order impulsive integro-differential equations in Banach spaces，Under the given conditions, using the cone drawing a fixed point theorem in cone sufficient conditions for the existence of positive solutions are obtained.

Boundary value problem;Impulsive differential equations;Positive solution ;Fixed-point theorem

2016-10-10.

广西自然科学基金项目资助(2014GXNSFAA118002)；广西高等学校高水平创新团队及卓越学者计划资助；广西高等数学与统计模型重点实验室开放基金课题研究计划资助.

饶显波(1992-)，男，四川达州人，广西师范大学数学与统计学院硕士研究生，研究方向：微分方程.

O175.8

A

1673-8462(2016)04-0057-07