用几何画板探究阴影部分的面积

湖北省十堰市第二中学 黄承洪

先看下面的题目：如图1:

图1

扇形OAB中，∠AOB=90°，OA=2，C是线段OB上的动点（包括端点O，B），以AC为直径作半圆，设图中阴影部分的面积为S，则S的取值范围是。

这是在2014年中考复习备考期间我校举行的一次模拟测试中我校一位老师出的一道填空题，并给出了如下解答过程：

(1)当C运动到点O时（如图2），

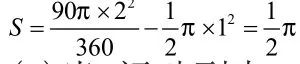
(2)当C运动到点B时（如图3），

∴S的取值范围为

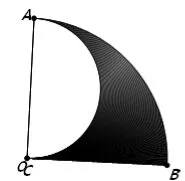
图2

图3

在改卷子的过程中有教师提出异议，认为除开端点外C点在移动过程中阴影部分由两部分组成，其中一部分减小时另一部分则增大，因此未必在端点处取得最大值和最小值，并试图通过设OC=x，建立S与x之间的函数关系式来说明，但最终却无功而返，只能按照所提供的答案进行试卷的批改和评讲。

为了探究题目的答案是否正确，我和其他老师一样也想从建立函数关系式的角度进行研究未果后，我想到几何画板除开具有画图功能外，还具有度量和计算的功能，那么能不能用几何画板来进行研究呢？下面就是我研究的过程。

一、先用几何画板画出图形，具体步骤如下

先作一个圆O，构造两条相互垂直的直径，得到圆上两点A，B，隐藏圆，依次选中O，A，B，构造圆上的弧，再依次作线段OA，OB得直角扇形OAB；

在线段OB上任意取点C，连结AC，构造AC中点，依次选中AC中点，C，A构造圆上的弧以OB为直径作半圆；（如图4）

图4

下面给需要的区域着色：

在半圆的上任取一点M，构造线段OM及与扇形OAB的的交点N，隐藏OM，构造线段MN，依次选中点M和线段MN，构造轨迹，最后隐藏点M、N和线段MN；

在上任取一点P，构造线段OP及与的交点Q，隐藏OQ，构造线段PQ，依次选中点P和线段PQ，构造轨迹，最后隐藏点P、Q和线段PQ；(如图5)

图5

此时我们移动点C，可以看到阴影部分的面积在变化

二、利用几何画板中的度量和计算功能探究阴影部分的面积

依次选中O、D、A，构造圆上的弧，再构造弓形内部，并度量面积；依次选中AC中点D、A，构造圆上的弧，再构造弓形内部，并度量面积；计算两个弓形的面积差；隐藏所作的弓形；

依次选中O、B、D，构造圆上的弧，再构造扇形内部，并度量面积；依次选中AC中点、C、D，构造圆上的弧，再构造弓形内部，并度量面积；选中O、C、D三点，构造三角形内部，并度量面积；计算扇形面积减去弓形的面积和三角形面积的差；隐藏所作的扇形、弓形和三角形；

计算1和2中的两个面积差的和；（如图6）

图6

此时我们运动点C，可以发现当点C运动到O时得图7：

图7

运动点C到点B得图8：

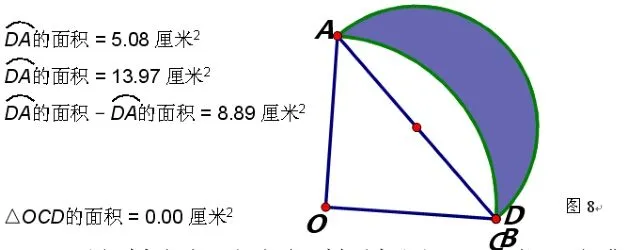
图8

比较图6和图7的结果，我们不难发现，当C点运动到O时阴影部分的面积并不是最小的。而运动点C可以发现当点C运动到点B是面积最大，至此我们可以确认该题提供的解法是没有依据的，答案也是错误的。而在运动点C的过程中，我们仔细观察可以发现当点C运动到OB中点时，面积似乎最小，但限于本人水平有限，无法从理论上加以说明，只能留着专家给予指正。