巧用课堂提问艺术培养学生思维能力

广东省信宜市教育城初级中学 梁恒华

一、创设激趣性提问，增强思维活动的愉悦氛围

有意识地提出问题，创造生动的愉悦情境让学生的思维拐个弯，问在此而意在彼，以激发学生的学习兴趣，而使学生带着浓厚的兴趣去积极思考。

例如，在学习“三角形的稳定性”时，可以这样提问：“为什么射击瞄准时，用手托住枪杆（此时枪杆、手臂与胸部构成三角形）能保持稳定？而能伸缩的铁门要做成平行四边形？”

又如，在学习“二元一次方程组”时，设置顺口溜提问：“鸡和狗99，300只脚满地走，问有几只鸡，几条狗？”问题一经提出，学生立即被这个有趣的提问所吸引。设置这样的提问，以“趣”引“思”，使学生处于兴奋状态和积极思维状态之中，诱发了学生主动学习的动机，增强了学生思维活动的愉悦氛围。再如，在学习“线段的垂直平分线”时，可这样设计课前提问：“如图，A、B、C三个村庄（呈三角形分布）合建一所学校，校址应选在何处才能使三个村庄到学校的距离相等呢？你能设计出一个方案吗？”问题一经提出，同学们马上想设计方案，从而激发学生的学习兴趣，思维处于愉悦状态，学生注意力非常集中。

二、迁移性提问，提供思维活动的导向

不少数学知识在内容和形式上有类似之处，它们之间存在着密切的联系。对于这种情况，教师可在复习旧知识的基础上有意识地设置提问，将学生已经掌握的知识和思维方法迁移到新知识的学习中去。

例如，教学一元一次不等式的解法时，教师首先提问：“解一元一次方程的步骤是什么?”然后再问：“同学们，你能用解一元一次方程的方法来解不等式

3x－5＜1和3(x－2)＞2(7－x)吗?”

如此设问，能使学生迫不及待地将已获得的知识和技能，从已知对象迁移到未知对象上去。

三、利用探索性提问，培养学生的创造思维

这种提问有利于培养学生创造思维，在学完一个数学问题后，再追问其思路是什么？是否能用其它方法去解决？引导学生的思维向深处和广处两方面发展。例如，证明方程（X－1）（X－2）=k2有两个不相等的实数根。此题的一般证法是：

∵已知方程为（X－1）（X－2）=k2方程变形得X2－3X＋（2－k2）=0其中a=1，b=－3，c=2－k2

∴b2－4ac=（－3）2－4×1×（2－k2）=1＋4k2

又∵k2≥0 ∴ 1＋4k2＞0即b2－4ac＞0

故问题得证。

问除此证法外，是否还有其它证法？此时学生就会发挥思维去另想新法。假设方程没有两个不相等的实数根，则已知方程有两个相等的实数根或没有实数根。

（1）若方程有两个相等的实数根

（2）若方程没有实数根，则b2－4ac＜0

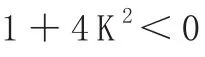
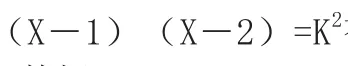
四、扩展性提问，培养思维活动的深刻性

思维活动的深刻性，体现在于善于深入地思考问题，找出客观事物的本质联系，揭示问题的本质。学生中有不良习惯的表征之一“眼高手低”，他们往往热衷于大题，难题的习作，疏忽对小题的思考与研究。作为教师适时地从小题入手，并进行扩展性提问设计，在师生互动中，让学生“小中见大”，揭示问题的本质规律，能培养学生思维活动的深刻性。

例如，在初三复习等腰三角形的性质时，

1.先出示一道题

已知等腰三角形的腰长为4，底边长为6，求周长。

2.然后由浅入深地进行扩展性提问

2．3 患儿治疗情况 在确诊的499例CH患儿中，1例非本病因死亡，其余498例均接受正规治疗和随防，诊治率为99．80%。329例在3岁时进行甲状腺功能、甲状腺B超复查、体格发育、智力发育等评估。其中有15例诊断为暂时性甲状腺功能减低症而永久停药，12例停药观察中，其余302例仍以药物治疗。31例PKU／BH4D中除5例因各种原因放弃治疗，其余的26例均接受规范的治疗和随防，诊治率为83．87%。串联质谱技术筛查出的11例遗传代谢病也得到及时治疗和随访。

变式提问1：已知等腰三角形的腰长为4，周长为14，求底边长。怎么办？

变式提问2：已知等腰三角形一边长为4，另一边长为6，求周长。怎么办？

变式提问3：已知等腰三角形一边长为3，另一边长为6，求周长。怎么办？

变式提问4：已知等腰三角形的腰长为x，求底边长y的取值范围。怎么办？

变式提问5：已知等腰三角形的腰长为x，底边长为y，周长为14。又怎么办？

请先写出二者的函数关系式，再在平面直角坐标系中画出它的图象。

通过这一组变式题组的扩展性提问及训练，对拓宽学生的“学习空间”，提高应变能力，培养思维的深刻性和灵活性有着重要的作用。

五、注意递进性提问，培养思维活动的连贯性

思维永远是由问题开始的，递进式巧妙地提问，往往能引起学生的强烈兴趣，一下子就把学生“抓”住。例如，在教“圆”这个概念时，一开始就问学生：“车轮是什么形状的？”这样，学生便不难地回答：“圆的。”又问：“为什么要造成圆形的呢？难道不能造成别的形状吗？比方说，造成三角形的、四边形的……”学生纷纷回答：“不能！”“它们无法滚动。”再问：“那就造成这样的形状吧（信手在黑板上画出一个椭圆和椭圆的中心），行吗？”学生始而茫然，继而大笑起来：“这样一来，车子前进时就会一忽儿高，一忽儿低。”然后紧接着进一步问:“为什么造成圆形就不会一忽儿高，一忽儿低呢?”最后学生终于找到答案:“因为圆形的车轮上一点到轴的距离是相等的。”至此，就自然引出圆的定义，这样的提问发人深思，趣味无穷，培养了学生思维活动的连贯性。

六、发散性提问，培养思维活动的灵活性

发散思维是一种创造思维，要引导学生多角度，多途径思考，纵横联想所学知识，以沟通不同部分的数学知识和方法，这对提高学生思维能力和探索能力是大有好处的。

例如，学习了全等三角形判定（边角边公理）的应用举例后，我进行发散性变式提问：

已知线段AD，AE⊥AD，DF⊥AD，垂足分别为A、D，且AE=DF，要在AD内取两点B，C，使EB=FC，应如何取？并加以证明。（即求证：EB=FC）。

学生议论，画图得出不同取法及证明途径

取法一、如图1、图2，取A B=D C，根据边角边公理可证△AEB≌△DFC，得EB=FC

取法二、如图3、图4，取AB=DC，可证△AEB≌△DFC得EB=FC我提问：图1-图4还有哪两条线段相等？（学生观察得，AC=DB）

图1、图2中的条件不变，还能引出什么结论？学生由已知知识自然地自编命题：（1）已知：AE⊥AD，DF⊥AD，AE=DF，AB=DC。求证：①∠E=∠F；②∠ABE=∠DCF（2）已知：如图1、图2中，AE⊥AD，DF⊥AD，AE=DF，AB=DC 求证：EB∥FC

如此进行发散性编题变式提问，学生从对公理的熟练掌握到知识的纵横联想应用自如了。学生思维的灵活性得到了培养。

七、铺垫性提问，扫除思维过程中的障碍

铺垫性提问就是对较为复杂的问题铺设“阶梯”，逐步深入，展开提问。把需要解决的问题分解成一系列子问题，通过解决子问题逐步消除初始状态与目标状态的之间的差异，从而使问题得到解决。因此，教师要围绕某个总问题的解决，而设计一些子问题作铺垫，来降低思维难度，扫除思维过程中的障碍。

例如，对于问题：在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，且，若关于x的方程有两个相等的实数根，又方程2x2－（10sinA）x＋5sinA＝0的两实数根的平方和为6，求△ABC的面积。

对于这个较为复杂的问题，可设计如下的问题链进行提问：

问题1：这道题要用到哪些知识？

问题2：在没有图形的情况下求三角形面积，猜想△ABC是什么三角形？

问题3：由哪个条件确定三角形的形状？

问题4：由哪个条件求出a、b边？

问题5：△ABC的面积可求了吗？怎样求？

这样来安排问题的提问，提问与思考同时进行，通过铺设问题“阶梯”，去层层深入，在学生积极思维的活动中让他们取得成功并饱尝“成功”的喜悦，能扫除思维过程中的障碍。

课堂提问是一门学问，更是一门艺术，提问不在于多，而在于问得奇、趣、妙；问得发人深思，引人入胜；问得难而有度，高而可攀。教师只要深入钻研教材，多联系实际，紧扣学生的求知心理，精心设计提问，就一定能优化课堂教学，培养学生思维能力，提高教学质量。