点云模型的五轴无干涉数控加工刀轨生成方法
张嘉炜,刘 威,袁铁军,张闯闯,谢竞尧
(1.苏州科技学院,苏州 215000;2.盐城工学院,盐城 224000)
点云模型的五轴无干涉数控加工刀轨生成方法
张嘉炜1,刘 威1,袁铁军2,张闯闯1,谢竞尧1
(1.苏州科技学院,苏州 215000;2.盐城工学院,盐城 224000)
摘 要:提出了一种对点云模型直接计算五轴数控加工刀轨的方法。所求出的刀轨无局部、全局干涉且具有较高的切削效率。首先将点云划分到立方体栅格中,对刀触点获取附近可能发生干涉的栅格,根据栅格中的点计算出无局部干涉的最小前倾角,基于此前倾角,再以迭代判断的方式计算出无全局干涉的最小旋转角,最后获得无干涉刀轴矢量。提出的方法避免了传统方法中曲面拟合这一复杂、耗时的过程,效率较高,对算例生成的无干涉刀轨验证了方法的可行性。
关键词:点云;五轴数控加工;无干涉;刀轨生成
0 引言
逆向工程中,点云模型通常由测量设备(如三坐标测量机、光学扫描仪)扫描实物获得,对点云生成数控加工刀轨,通常先对点云拟合曲面或者构造网格模型,再对曲面或网格生成加工刀轨,然而这是一个复杂、费时的过程。直接对点云生成数控加工刀轨,可以避免曲面重构,大幅减少计算数控加工刀轨的工作量[1~7]。
五轴数控加工与三轴相比,具有复杂零件加工能力强、加工效率高、表面质量好等优点。五轴加工由于两个偏转轴的加入,刀轴运动十分灵活,容易发生干涉。干涉主要有局部干涉和全局干涉两种,前者包括刀底干涉和曲率干涉,分别由于前倾角不足和曲率不匹配造成,会引起加工零件的过切,全局干涉是指加工零件、刀杆、夹具、机床之间的碰撞,容易造成零件、机床的损坏。五轴干涉处理较为复杂,许多学者对此进行了研究[8~15]。Kim[9]等针对NURBS曲面提出通过密切圆与曲面三阶相切来避免局部干涉,通过刀具和曲面双切触来避免全局干涉。Lin[10]假设连续相邻刀触点的无干涉区域是连续的并在其中取点进行3次B样条曲面插值,求出无全局干涉的刀轴区域,适用于干涉区域变化平缓的情况。梁全[12]针对闭式叶轮提出了一种干涉碰撞的避让规划算法。章永年[13]通过构建人工势场模型,将干涉处理转化为运动学中平衡位置的求取问题。以上是对曲面模型的研究,点云方面,谢叻等[14]通过计算点云的法矢量和曲率确定切削步长和行距,由刀触点计算刀位点并进行干涉检查,得到了无干涉的加工刀轨。孙殿柱等[15]根据点云型面特征规划驱动刀轨,获取瞬时加工区域中数据点计算刀位点,选取刀轴正向最高点作无干涉刀位点。
目前大部分研究都是针对曲面,由于点云离散的特点,曲面方法难以使用,本文提出一种对点云快速生成五轴刀轨的方法,以刀触点截面线法构造刀触点,对每个刀触点构造局部坐标系,获取可能发生干涉的点,然后分别计算无局部、全局干涉时的最小刀轴偏角,最后获得切削效率较高的无干涉刀轴矢量和刀位点。
1 无干涉刀轨生成
1.1数据预处理
点云模型由海量离散点组成,为了便于管理点和提高算法效率,本文将点云划分到立方体小栅格中。首先获取每个点的坐标,得到其最大、最小值(xmax、ymax、zmax、xmin、ymin、zmin)并以此构造长方体包围盒,设立方体栅格的长度为Lcell,可取点平均距离的3~5倍,栅格在X、Y、Z方向的个数可由式(1)求出。对于任意数据点P(px,py,pz),所在栅格的序号可由式(2)求出,i、j、k分别为该点所在立方体的X、Y、Z轴方向栅格的序号。对每个点计算出所在栅格的序号,并将点信息保存到所在栅格中。

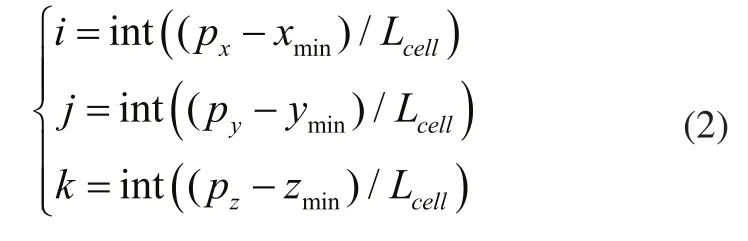
1.2局部干涉处理

图1 局部坐标系和局部干涉示意图
设刀具绕X和Z轴旋转的偏角分别为前倾角α和旋转角ω,进给、行距方向分别为X和Y轴的正方向,采用文献[5]中适用于点云的刀触点截面线法规划刀触点,获得第i行刀触点集合为第j个刀触点,本文以为例给出干涉处理方法,过程如下。

平底铣刀等效切削半径RE可由文献[16]中的式(4)求出,前倾角、旋转角越小,等效半径越大,切削效率越高。为了获得大的等效半径,前倾角、旋转角应取无干涉最小值。如图1(a)所示,PCr为刀具底面在ZL方向上的最高点,所有zL坐标小于PCr大于0的点都有可能与刀具发生局部干涉,根据此条件检查长方体内所有数据点的局部坐标(xL,yL,zL),将满足式(5)的所有数据点记为集合PL,其余所有点有可能发生全局干涉,记为集合PG。获取集合PL后,可按照以下流程计算无局部干涉最小前倾角αmin:

Step1:令α= α0,α0为用户允许的最小前倾角。


且满足式(8),即在刀具底面之上且到刀轴中心距离小于刀具半径,则发生干涉,运用式(9)计算出无干涉时的最小前倾角αi,其中点B是位于刀轴上的垂足,如图1(b)所示;否则点不会与刀具发生干涉,无干涉最小前倾角为α0,即αi= α0。


Step4:按照Step3遍历PL中的每一个点,所有点无干涉最小前倾角的最大值可满足所有点无局部干涉,即
通过以上流程即可获取无局部干涉时的最小前倾角αmin,刀轴矢量由前倾角和旋转角共同定义,下一节将给出根据αmin计算无全局干涉最小旋转角的过程。
1.3全局干涉处理
通过上节获得可能发生全局干涉的所有数据点集合PG和无局部干涉的最小前倾角αmin,本节以预设刀轴矢量初值、迭代旋转角并判断的方式计算无干涉的旋转角最小值,将α= αmin和ω=0代入式(6)构造初始刀轴矢量,通过逐渐增大旋转角的方式来调整刀轴矢量,直至与所有点都不发生全局干涉,计算流程如下:
Step2:令i=i+1,以α= αmin和ω=±i⋅∆ ω构造两个新的刀轴矢量
Step3:将集合PG中的点依次代入式(9),计算出点PGj到刀轴Ti1(或Ti2)的距离,若所有点到刀轴的距离都大于刀具半径R与安全距离ls之和,即则(或)就是要求的无干涉刀轴矢量,流程结束;否则转到Step2。

2 算例
所提出的方法已在Visual C++ 6.0和Opencascade 6.2.0平台上完成开发,为了验证其可行性,对图2所示的点云计算五轴刀轨。点云包含200631个点,尺寸为200mm×151mm×67mm,由1个长方体、两个球体组成的障碍物点云和加工表面点云组成,刀具选择直径16mm的平底铣刀进行计算刀轨,其中的两行刀轨如图3所示,从图3(a)可看出刀轨避开了障碍物,实现了无全局干涉,从图3(b)可看出点云无过切,实现了无局部干涉。

图2 点云模型

图3 算法求出的刀轨
3 结论
本文提出了一种对点云直接计算五轴无干涉刀轨的方法,此算法省去了构造曲面这一复杂的中间过程,可对刀触点快速求出无干涉刀位点和刀轴矢量,采用基于计算点到刀具距离的方法计算无干涉的最小前倾角和旋转角,并以此定义刀轴矢量和计算刀位点,以获得切削效率较高的加工刀轨。该方法所求出的刀轴矢量虽然满
【】【】足无干涉,但不一定是理论最优解,在未来的研究中,可对干涉问题作进一步研究,对每个刀触点计算出所有无干涉刀轴矢量(即刀轴矢量可行域)再进行优化,最终获得理想的刀轨。
参考文献:
[1] Lin AC, Liu HT.Automation generation of NC cutter path from massive data points [J].Computer-Aided Design,1998,30(1):77-90.
[2] Yau HT, Hsu CY. Generating NC tool paths from random scanned data using point-based models[J].The International Journal of Advanced Manufacturing Technology,2009,41(9-10):897-907.
[3] Park SC, Chung YC.Tool-path generation from measured data[J]. Computer Aided Design,2003,35(5):467-475.
[4] Feng HY,Teng Z. Iso-planar piecewise linear NC tool path generation from discrete measured data points[J].Computer-Aided Design,2005,37(1):55-64.
[5] 刘威,周来水,安鲁陵.截面线等误差步长法计算点云刀具路径规划 [J].机械科学与技术,2013,32(6):824-828.
[6] Liu W,Zhou LS,AN LL.Constant scallop-height tool path generation for three-axis discrete data points machining[J].The International Journal of Advanced Manufacturing Technology,2012,63(1-4):137-146.
[7] 吴福忠,华小洋,连晋毅.测量点数据等残留高度刀具路径规划[J].计算机辅助设计与图形学学报,2007,19(12):1618-1623.
[8] Tang TD. Algorithms for collision detection and avoidance for five-axis NC machining: A state of the art review[J].Computer-Aided Design,2014,51(6):1-47.
[9] Kim YJ, Elber G, Bartoň M,Pottmann H.Precise gouging-free tool orientations for 5-axis CNC machining[J].Computer-Aided Design,2015,58(1):220-229.
[10] Lin ZW,Shen HY, Gan WF. Approximate tool posture collisionfree area generation for five-axis CNC finishing process using admissible area interpolation[J].The International Journal of Advanced Manufacturing Technology,2012,62(9-12):1191-1203.
[11] Hu PC, Tang K, Lee CH. Global obstacle avoidance and minimum workpiece setups in five-axis machining[J].Computer-Aided Design,2013,45(10):1222-1237.
[12] 梁全.叶轮五坐标数控铣削CAM和CNC关键技术的研究[D].哈尔滨:哈尔滨工业大学,2009.
[13] 章永年.五轴数控加工中无碰刀具轨迹生成算法的研究[D].南京:南京航空航天大学,2012.
[14] 谢叻,魏安顺,周印.基于激光测量点云数据的五坐标加工刀轨生成[J].上海交通大学学报,2004,38(8):1378-1381.
[15] 孙殿柱,崔传辉,康新才,王超.基于散乱点云数据的五轴数控加工刀轨生成算法[J].农业机械学报,2012,43(5):226-229.
[16] Can A, Ünüvar A.A novel iso-scallop tool-path generation for efficient five-axis machining of free-form surfaces[J].The International Journal of Advanced Manufacturing Technology,2010,51(9):1083-1098.
5-axis collision-free NC tool path generation method for point clouds
ZHANG Jia-wei1, LIU Wei1, YUAN Tie-jun2, ZHANG Chuang-chuang1, XIE Jing-yao1
中图分类号:TP391.73
文献标识码:A
文章编号:1009-0134(2016)05-0158-04
收稿日期:2016-02-15
基金项目:江苏省高校自然科学研究面上项目(14KJB460027);江苏省科技计划项目(BY2015057-22);江苏省大学生创新项目(201410332032Y);苏州科技学院科研基金(青年项目)
作者简介:张嘉炜(1994 -),男,本科,主要研究方向为CAD/CAM和数控加工。

