主动四轮转向车辆的分数阶鲁棒控制研究

田 杰，李守泽，王 玉，陈 宁

（南京林业大学　汽车与交通工程学院，南京 210037）



主动四轮转向车辆的分数阶鲁棒控制研究

田 杰，李守泽，王 玉，陈 宁

（南京林业大学汽车与交通工程学院，南京 210037）

摘 要：首先对主动四轮转向车辆线性二自由度模型进行了输入输出解耦，分别得到了横摆角速度和质心侧偏角的传递函数，并构造了理想参考模型。为了减小系统性能受车辆参数的不确定性、未建模动态等因素的影响，在解耦的基础上引入了分数阶PIλDµ鲁棒控制方法，并通过优化得到了控制器的五个设计参数以保证该系统在要求的频域内具有很好的鲁棒性。通过MATLAB/ Simulink对线性和非线性系统进行了仿真分析，结果表明，基于解耦的分数阶鲁棒控制能使得主动四轮转向车辆很好地跟踪其参考性能，且具有良好的鲁棒性。

关键词：主动四轮转向；解耦；分数阶PIλDµ控制器；鲁棒性

0　引言

主动四轮转向（Active Four-Wheel-Steering，4WS）技术是主动底盘控制技术的重要组成部分，通过后轮直接参与对车辆侧向及横摆运动的控制，可有效改善车辆高速时的操纵稳定性和低速时的机动灵活性。在4WS车辆的控制方法上，先后出现了许多控制方法和控制策略，如前馈控制，前馈加反馈控制，μ综合反馈控制、最优线性二次调节器控制、滑模变结构控制、模糊控制以及解耦控制等［1］。相关研究证明，对车辆的转向特性进行解耦控制有利于提高车辆的安全性和行驶性。对横摆运动和侧向运动的单独控制可提高车辆的操纵稳定性，并保证驾驶的安全性和精确的轨迹跟踪性［2，3］。本课题在对主动四轮转向车辆模型进行解耦的基础上，设计了分数阶鲁棒控制器以达到改善车辆操纵稳定性的目的。

1　车辆模型

1.1四轮转向车辆的动力学模型

只考虑车辆沿y轴的侧向运动与绕z轴的横摆运动，可得车辆运动微分方程［1］：

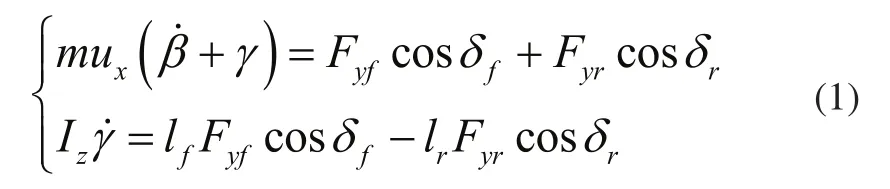
其中，m为汽车质量，Iz为车辆对Z轴的转动惯量，ux为汽车质心处的纵向速度，lf和lr分别为质心到前后轴的距离，δf和δr分别为前后轮转角，β为质心侧偏角，γ为横摆角速度，Fyi为前后轮胎的侧偏力（i=f，r）。采用魔术轮胎［4］得到的前后轮侧偏力如下：

则：

1.2参考模型

通常的做法是定义一阶系统作为参考模型［5］，且质心侧偏角为零。但研究发现，基于使汽车转弯时的质心侧偏角保持为零的4WS车辆具有过大的不足转向特性，并且零侧偏角会使驾驶员因与普通车辆驾驶感觉上的差异而引起不适应［1］。考虑到对于普通的前轮转向车辆而言，车辆在轮胎附着条件允许的情况下如果能按照线性二自由度车辆模型所描述的转向特性运动，汽车运动将是比较理想的，也是稳定的。因此，此处将具有理想匀速圆周运动的线性二自由度车辆特性作为参考模型。设则相应的状态方程表示为：

其中，lfd和lrd分别是质心到前后轴的距离，βd是质心侧偏角，γd是横摆角速度。

尽管具有中性转向特性的车辆在路径跟踪上优于具有适度不足转向特性的车辆，然而其质心侧偏角却偏大。同时，不同的驾驶员对质心侧偏角的期望值也各有不同。为此，本文在具有中性转向特性的线性二自由度车辆模型的基础上，对其输出的质心侧偏角进行降幅滤波以得到理想参考模型。而其降幅滤波的程度可依驾驶员的要求而实时调整。此处，降幅滤波器的传递函数为：

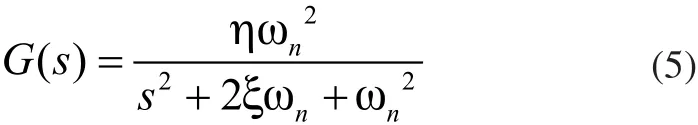
其中，η和ξ分别为系统的系数和阻尼系数，ωn为系统圆频率。通过调整ωn可以方便地调整质心侧偏角的幅值。

2　控制系统设计

此处主要研究两种控制策略，其中一种是基于参考模型的最优控制，另一种是基于理想参考模型的分数阶鲁棒控制。

2.1最优控制器设计

基于参考模型的最优控制的目标是寻求uc（t）使得性能指标J最小。

其中，权重系数Q≥0，输入权重系数R＞0。假设A和B是可控的，A和C是可观的，则（6）的控制输入uc=-Kcx，其中，Kc是最优反馈系数矩阵，且Kc=R-1BTP；P是如下所示黎卡提方程的解。

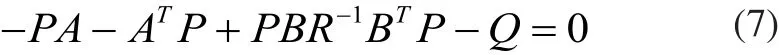
2.2分数阶鲁棒控制器设计

考虑到4WS系统受到诸如参数的不确定性、未建模动态等因素的影响，文中基于分数阶微积分理论，设计了一种新型的分数阶PIλDµ控制器，以实现4WS车辆跟踪理想模型的同时提高系统的鲁棒性。该控制策略主要是根据实际车辆模型和理想参考模型的状态变量差值来修正四轮转向系统的前轮和后轮转角，以确保实际车辆的质心侧偏角和横摆角速度能跟踪理想参考模型值，控制框图如图1所示。其中，输入输出解耦的目的是使得横摆角速度和质心侧偏角分别受控于两个新引入的输入变量u1和u2。

2.2.14WS线性车辆模型的解耦

由线性车辆模型（3）不难得出其传递函数为：

其中：

图1　4WS分数阶鲁棒控制框图

可见，汽车的横摆角速度γ和质心侧偏角β同时受控于前、后轮转角δf和δr。因此，非常有必要将汽车的横摆角速度和质心侧偏角解耦，以实现对理想参考模型的良好跟踪。

为了让横摆角速度和质心侧偏角分别受控于相互独立的两个输入变量，不妨引入u1和u2。从图3可以看出，前、后轮转角δf和δr与新引入变量u1和u2的关系如下：

其中：

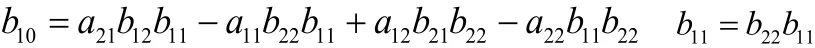
2.2.2分数阶鲁棒控制器设计

分数阶PIλDμ控制器对系统参数的不确定性不敏感，且比PID控制器多了两个控制参数，因此鲁棒性较好且设计较灵活。其传递函数通常表述如下［6］：

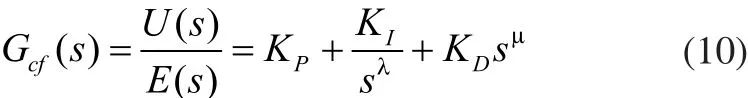
其中，KP、KI和KD分别为比例系数、积分系数和微分系数，λ和µ分别为积分阶次和微分阶次。

3　仿真结果分析

图2　四轮转向车辆的前轮转角输入信号

3.1线性模型的仿真分析

前轮转角输入相同的情况下，对于线性模型改变其车辆参数，分别采用最优控制和分数阶鲁棒控制所得到的仿真曲线如图3和图4所示。

图3　最优控制时线性车辆的响应曲线

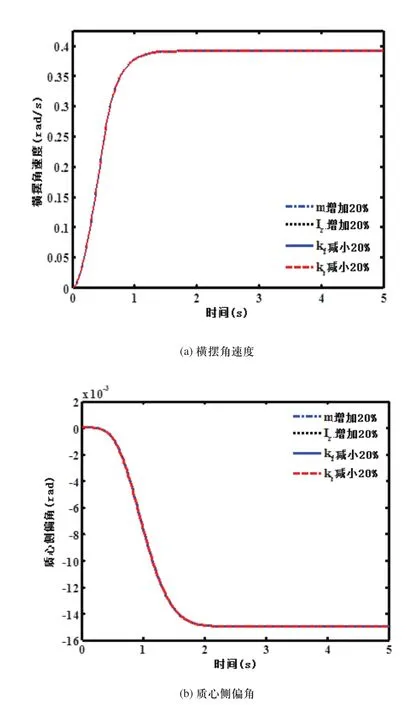
图4　分数阶鲁棒控制时线性车辆的响应曲线

从图3和图4可以看出，采用分数阶鲁棒控制的线性车辆的鲁棒性很好，而采用最优控制的线性车辆的横摆角速度曲线有小幅变化，尤其是质心侧偏角的变化幅值很明显。

3.2非线性模型的仿真分析

前轮转角输入相同的情况下，对于非线性模型改变其车辆参数，分别采用最优控制和分数阶鲁棒控制所得到的仿真曲线如图5和图6所示。

图5　最优控制时非线性车辆的响应曲线

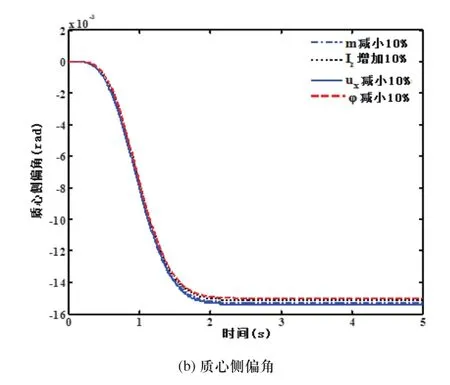
图6　分数阶鲁棒控制时非线性车辆的响应曲线

从图5和图6可以看出，非线性车辆采用最优控制时横摆角速度基本不随参数m、Iz和ux的变化而变化，而质心侧偏角却变化很大，尤其是附着系数ϕ的些微变化甚至导致了车辆的不稳定；而采用分数阶鲁棒控制的非线性车辆却表现出了良好的鲁棒性。

4　结论

通过仿真结果可知，基于解耦的主动四轮转向车辆分数阶鲁棒控制具有良好的鲁棒性，可有效地抑制系统参数的不确定性和未建模动态等因素对车辆性能的影响。

参考文献：

［1］ Chen N， Chen N，Chen YD.et al. On fractional control method for four-wheel-steering vehicle［J］.SCI China Ser E-Tech Sci， 2009，52（3）：603-609.

［2］ N. Matsumoto， M. Tomizuka.ehicle lateral velocity and yaw rate control with two independent control inputs［J］.ASME Trans. J. Dynamics， Measurement，Control，1992，114：606-613.

［3］ J. Ackermann. Robust decoupling， ideal steering dynamics and yaw stabilization of 4WS car［J］.Automatic，1994，30（11）：1761-1768.

［4］ Marino and Cinili， 2009 Marino， R.， and Cinili， F.. Input-Output decoupling control by measurement feedback in four-wheelsteering vehicles［A］.IEEE Transactions on Control Systems Technology［C］.2009，17（5）：1163-1172.

［5］ Canale M， Fagiano L.Stability control of 4WS vehicle using robust MC techniques［J］.Vehicle System Dynamics，2008，46（11）：991-1011.

［6］ Tian， J.， Wu，J.， Chen， N.， Luo， S.. Fractional PID Control for Steer-by-wire System［J］.Advanced Materials Research，2011，279：423-428.

Fractional robust control research of active 4WS vehicle

TIAN Jie， LI Shou-ze， WANG Yu， CHEN Ning

中图分类号：U463.4

文献标识码：A

文章编号：1009-0134（2016）05-0150-05

收稿日期：2016-02-04

基金项目：国家自然科学基金项目（11272159）；国家青年自然科学基金项目（51305207）；江苏省政府留学基金项目（JS-2014-014）

作者简介：田杰（1971 -），女，湖北人，副教授，博士，研究方向为车辆系统动力学及控制、汽车设计CAD/CAE。