一种新型连续可调光程发生系统安装误差研究

丁红昌，陈小杰，韦湘宜，曹国华

（长春理工大学　机电工程学院，长春 130022）



一种新型连续可调光程发生系统安装误差研究

丁红昌，陈小杰，韦湘宜，曹国华

（长春理工大学机电工程学院，长春 130022）

摘 要：针对传统的光程发生系统所具有的光程不可调、安装精度要求过高等问题。首先提出了一种光程连续可调的光程发生系统。该系统由3个反射镜片组所组成，光束从一端入射，经过3个镜片组的连续反射，从另一端出射。利用矩阵变换建立出射光线和入射光线的函数关系式，该表达式说明该系统具有连续可调、分辨率高等特点。在此基础上并进一步推导出总光程表达式opd= G（ h， R， d， ru， rsd ）。传统的光程发生系统所具有的安装精度要求过高问题，即必须保证上一个镜片的安装精度才能进行下一个镜片的装调，镜片的装配精度具有耦合性。为此首先解算出一个最佳入射角度，然后建立以3个镜片的平移、旋转的安装允许安装误差为目标函数的非线性有约束规划模型，利用遗传算法求出3个镜片单独的最佳容差范围，从而实现了镜片安装精度的解耦。实际装调中，只需分别保证3个镜片的装调精度在各自的允许安装误差带内即可保证总体的安装精度。该模型实现了镜片装调的解耦对于实际光学系统的安装调试具有很好的指导意义。

关键词：连续可调光程发生系统；安装误差；误差分析；优化规划；遗传算法

0　引言

光程发生系统在航空航天、环境监测、通信等到很多场合具有重要意义，传统的光程发生系统只能利用定长光线产生固定的光程［1］，其光程不可调节。同时镜片安装时耦合性过高，首先要保证上一个镜片的安装精度才能进行下一个镜片的安装。为了解决这两个问题，本文首先提出一种光程连续可调的光程发生系统。接着为了解决安装时过高的安装耦合性，首先解算出最佳的入射角度，接着建立了以3个镜片的位移、旋转安装允许公差为自变量，最佳容许安装误差为目标函数的约束规划模型。求解此模型得到3个镜片分别的最大安装容许公差，即实现了镜片安装精度要求的解耦。应用此模型，实际安装调试中只需分别保证单个镜片在允许内的安装容许公差带内，即可保证总体的安装精度。

1　连续可调光程发生系统模型建立

连续可调光程发生系统的主要由三个具有相同的曲率半径的反射镜组成。光线从一端射入，经过反射镜组的多次反射之后从另一端射出。其示意图如图1所示。通过调节右边两个镜片的垂直距离来改变光程。

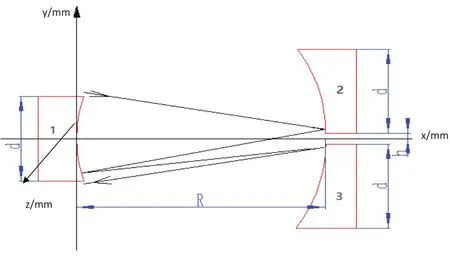
图1　光程发生系统示意图

1.1连续可调光程发生系统的模型建立

建立如图1所示的坐标系，入射光线（rux0，ruy0，ruz0）经过3个镜片组的连续反射得到出射光线（chux，chuy，chuz）。联立镜片方程与光线方程求解出入射光线与镜片的交点（xi，yi，zi）。

其中，i表示第i次入射，j取1、2、3分别表示1、2、3镜片。Hj（R，h，d）表示第j个镜片的方程。

由旋转变换矩阵可以求得入射光线（ruxi，ruyi，ruzi）经过镜片反射之后得到的新入射光线（ruxi+1，ruyi+1，ruzi+1）［2］。由欧式空间距离公式可得光程表达式为：

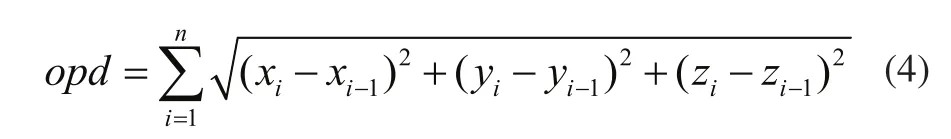
1.2连续可调光程发生系统的最佳入射方向向量

在理想情况下，镜片安装没有安装误差。可以求得容许入射光线变化最大的最佳入射角度。在此角度下，镜片的入射光线在容许的偏转范围内，出射光线都可以被接收器接收到。构造出以最佳接收效果为性能指标的约束优化模型，根据系统本身具有的物理特性列写约束方程。求解此优化模型即可得出最佳入射角度。

以最佳接受效果为性能指标的目标函数：

根据接收器接受范围，镜片尺寸参数列出约束条件：

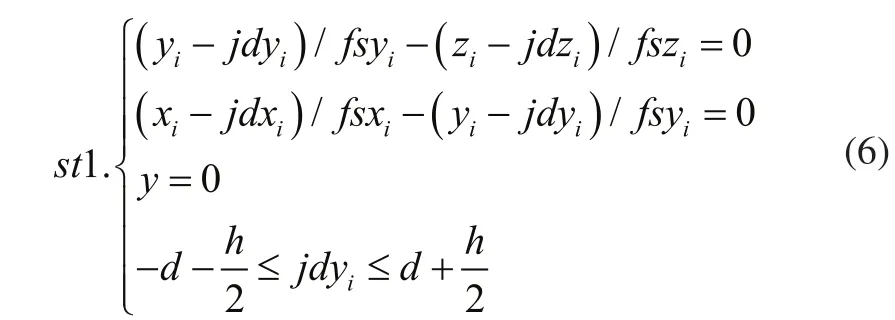
其中fs=（fsxi，fsyi，fszi）为方向向量，（jdxi，jdyi，jdzi）为第i次的入射向量与镜片的交点。即fs满足：

求解此非线性有约束优化模型即可求出最佳入射向量

2　镜片组实际安装最大容许误差研究

实际工程中，镜片安装总有安装误差。传统的镜片安装往往需要保证上个镜片的装配精度，才能装配调整下一个镜片，装配精度要求过高。本文建立的数学模型能够在保证总体安装精度要求下，求解出单个镜片能够达到的的最大容许误差。实际装调中，只需满足单个镜片的装配精度，即可满足总体装配精度。

仿照第一节最佳入射向量的求解，可以类似求解出在保证总体安装精度的前提下，3个镜片分别独立允许的最大安装允许误差［4］。

保证总体安装精度下，衡量3个镜片最佳独立安装允许误差目标函数：

目标函数分为两项，其中F1是用来衡量每个镜片安装误差分布的分散程度，F2是用来衡量其允许的安装误差的大小。其中（xi，yi，zi，rxi，ryi，rzi）为镜片i的最佳位置。定义（∆xi，∆yi，∆zi，∆rxi，∆ryi，∆rzi）为第i个镜片安装时所允许的最大误差。

约束条件：

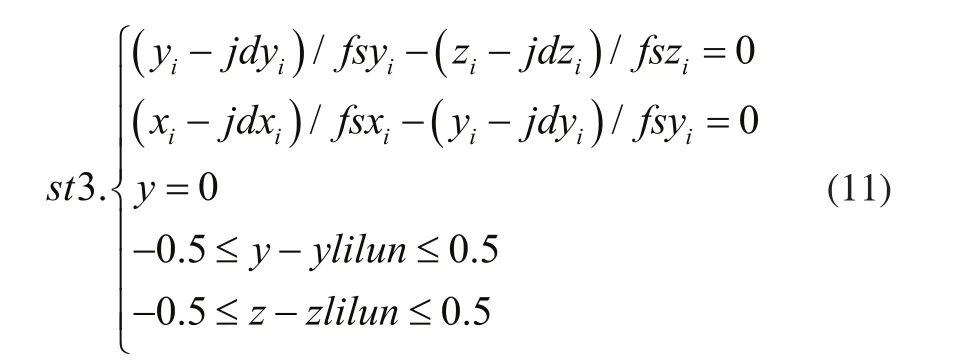
其中（xlilun，ylilun，zliun）为理想安装下的最佳位置出射光线与接收器所在平面的交点。

求解此优化模型即可得出单个镜片分别所允许的最大安装误差。应用此模型，只需保证每个镜片在所允许的安装误差带内，即可保证总体的安装精度，即实现了镜片安装精度的解耦。

3　实例验证和结果分析

以接收器半径大小为0.5mm对该模型进行验证，实例中的参数如表1所示。

表1　实例验证中参数

3.1光程表达式

联立方程（1）～（11）求出光程的表达式如下形式：

其中，（xi，yi，zi）为第i次入射光线与镜片的交点。显然（xi，yi，zi）与镜片间的距离h有关。图2是其MATLAB求解仿真示意图。

图2　MATLAB仿真求解示意图

3.2单个镜片的安装容许公差带

将参数代入第三节的优化模型即可求解出在保证总体安装精度下，3个镜片分别的安装容许公差带。由于本问题的约束函数较复杂，传统的优化算法在此不适用。为此采用遗传算法求解［6］。联立式（8）～式（10），利用MATLAB即可求解出3个镜片各自的安装容许公差带。黑色矩形区域内即为每个镜片的平移和旋转安装容许公差带。

图3　镜片1安装容差范围

图4　镜片2安装容差范围

图5　镜片3安装容差范围

3.3结论分析

由图（3）～图（5）可以清晰地看出在保证总体安装精度要求下每个镜片所允许的安装公差带。黑色矩形区域代表着每个镜片XYZ轴所允许的最大平移和旋转安装公差带。相对于传统的必须保证上一个镜片装调精度才能装调下一个镜片的装配方式，本文提出的装配方式，只需每个镜片的安装误差都在各自黑色矩形容许安装误差区域内，即可保证总的装配精度。显然后者装配简单，这对于实际装调具有重要指导意义。

4　结束语

为了解决传统光程发生系统具有的光程不可调和镜片安装调试困难两个问题。首先提出了一种连续可调光程发生系统，推导出光程和镜片组距离h的表达式。通过调整h的大小，即可改变光程的大小。接着为了解决传统的镜片安装调试困难，即必须保证上一个镜片的安装镜片，才能安装调试下一个镜片。本文提出的模型只需保证每个镜片在各自的允许公差带内，即可保证总的安装精度要求。最后通过仿真实验验证了该模型的实用性，实际应用中，只需保证每个镜片在各自的允许安装黑色矩形误差带内，即可保证总的安装精度要求。该模型对于实际的装配调试具有很好的指导意义。

参考文献：

［1］ 史洁琴，何珂，徐永.光纤基线标定激光测距仪方法研究［J］.南京航空航天大学学报，2002，（44）16：830-834.

［2］ 王卫东.计算机图形学基础［M］.西安电子科技大学出版社，2009（9）.

［3］ 乔达诺（Giordano，F.R.）等.数学建模［M］.北京：机械工业出版社， 2003.05.

［4］ Francis S Hill Jr， Stephen M Kelley. 计算机图形学（OpenGL版）［M］.胡事民，刘利刚，等译.3版.清华大学出版社，2009.

［5］ （日）玄光男，（日）遗传算法与工程优化［M］.程润伟，于歆杰，周根贵，译.北京：清华大学出版社，2004.01.

［6］ 黄席樾，向长城，殷礼胜，著.现代智能算法理论及应用（第2册）［M］.北京：科学出版社，2009.

Erection tolerance analysis of a new continuous and adjustable optical path system with high resolution

DING Hong-chang， CHEN Xiao-jie， WEI Xiang-yi， CAO Guo-hua

中图分类号：O439

文献标识码：A

文章编号：1009-0134（2016）05-0155-03

收稿日期：2016-02-15

基金项目：光频梳激光位移传感器设计开发（20140203017GX）

作者简介：丁红昌（1980 -），男，辽宁抚顺人，讲师，博士，主要从事光电在线检测技术方面的研究。