基于在线回声状态网络的变形数据预测分析

单　毅　杨建伟　王新志

1　南京信息工程大学数学与统计学院，南京市宁六路219号，210044 2　南京信息工程大学遥感学院，南京市宁六路219号，210044

基于在线回声状态网络的变形数据预测分析

单毅1杨建伟1王新志2

1南京信息工程大学数学与统计学院，南京市宁六路219号，210044 2南京信息工程大学遥感学院，南京市宁六路219号，210044

摘要：结合Kalman滤波与回声状态网络，将在线回声状态网络算法应用于变形数据预测。回声状态网络的输出权值通过Kalman滤波训练，直接对网络的输出权值进行在线更新，克服了传统递归网络需要收集大量样本后才能进行拟合预测的缺陷，同时也保证了预测精度。实例计算验证了该方法的有效性。

关键词：在线学习；变形观测数据；回声状态网络；Kalman滤波

神经网络以其强大的自适应性和联想记忆能力，广泛应用于变形数据的建模预测[1-4]。回声状态网络(ESN)是近年来兴起的一种非线性映射能力很强的神经网络，其采用求伪逆的训练方法，可避免基于梯度下降算法的一些缺陷[5-6]。目前包括ESN在内的传统神经网络大多采用离线学习方式，在大量样本提交后才会调整网络参数。然而变形数据在某些情况下不容易观测得到，导致没有足够的观测值供离线学习[1]，且离线学习需要占用大量的计算资源，不能实时调节相关参数[7]。此时，需要一种在线预测方法，在相对节省存储空间的前提下，对快时变的变形数据作出准确预报。Kalman滤波是一种在线预测算法，但其限制条件苛刻，要求系统模型精确且系统误差模型和观测误差模型已知[8]， 这在实际应用中很难满足。基于此，韩敏等[7]提出一种在线ESN。本文将这种在线ESN应用于变形数据的预测，采用Kalman滤波实时更新ESN的输出权值。相比基于求逆或者梯度下降的离线训练方式，该算法训练效率高，能动态调整网络权值，从而提高网络在线预测性能。对淮南市潘一东矿的地表沉降数据进行测试，实验结果证明了该算法的有效性。

1在线回声状态网络预测算法

1.1回声状态网络

ESN是一种新型递归网络[5-6]，包含输入层、输出层和储备池3个部分，各部分通过连接权值连接，其结构如图1所示。在n时刻向网络输入样本u(n)后，形成如下动态递归系统：

(1)

式中，Win是输入层与储备池的连接权值矩阵，W是储备池内部神经元之间的连接权值矩阵，Win和W都在训练前随机产生于(-1，1)之间并且之后不再变动。在离线学习的情况下，储备池与输出层之间的连接权值Wout需要根据求伪逆的方法得出[6]，这可能占用大量的存储空间和计算资源。本文使用在线ESN进行变形数据的实时预测。

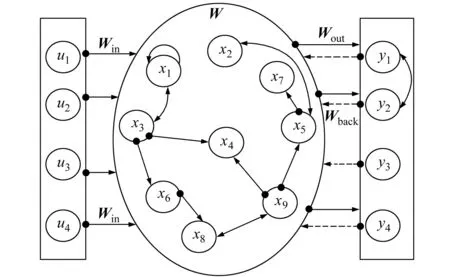
图1　回声状态网络基本结构图Fig.1　The structure of ESN

1.2基于Kalman滤波法的ESN输出权值训练

韩敏等[7]提出用Kalman滤波训练ESN的在线ESN算法，将ESN的状态空间转化为Kalman滤波的形式，即把输出权值Wout视为Kalman滤波状态值，根据ESN输出权值的变化特性，将状态转移矩阵设置为单位矩阵，则状态转移方程为：

(2)

(3)

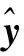
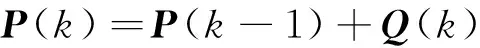
(4)

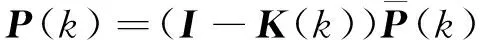
(5)

式中，R(k)、Q(k)分别为测量噪声和过程噪声的协方差矩阵，K(k)为Kalman滤波增益，A(k)是对增益矩阵的调整：

(6)

(7)

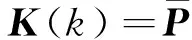
(8)

综上,可利用式(2)～(8)在线更新ESN的输出权值，并计算网络输出。

2工程实例分析

2.1工程概况与精度检验指标

潘一东矿位于淮南市北部，为掌握采矿期间地表沉降状况，对采矿区域地表布设CORS自动化监测系统。系统由1个基准站和6个监测站组成，采样间隔为30s，利用3G和无线网桥将数据实时传回数据中心。以6号监测站1个月数据为例进行分析，采用均方误差(MSE)评判预测模型的精度：

(9)

2.2实验验证及分析

在线ESN算法流程见图2。

图2　预测模型流程Fig.2　The flow chart of model predicting

创建网络后，设置输入层和输出层神经元个数为1，储备池神经元个数为600，W(储备池内部连接权值矩阵)谱半径小于1。

收集变形监测点1个月的原始监测数据，测量单位为m。在监测过程中发现，数据的整数部分没有变化，而小数部分变化剧烈，并呈现很强的非线性特征。从预测精度出发，将小数部分的变化作为重点研究对象。监测数据有x、y(水平)、z(高)3个维度方向，本文仅选z方向数据为例。由于该沉降数据变化范围在cm级且非线性特征较强，现有的算法模型很难将全部变形情况精确地预测出来[9-10]。根据该组数据的特点，设定其噪声误差服从均值为0、方差为0.001 m的高斯分布[11]，初始误差方差设定为0.001，状态转移矩阵和观测矩阵都设定为单位阵。

针对同一天的变形数据，分别使用在线ESN(图3)和Kalman滤波预测(图4)。从图3可以看出，由于在线ESN可以依据数据的实时变化作出预测，预测结果不易被异常点(图中第303个数据)干扰，较适合于短期预测。在线ESN的预测基本上遵循数据的变化情况，虽然在细节上不完全符合真实的振幅，但变化的方向基本吻合。图4中，Kalman滤波虽然也预测出了大致的变化趋势，但是没有描绘出变化细节。选用离线BP网络作为比较对象，使用同一天前600个观测数据作为训练集，预测后200个数据的变化情况，结果见图5。可以看出，BP网络虽然有时预测效果不错，但存在预测不稳定的情形，有时预测曲线的变化甚至与真实数据变化情况相反。

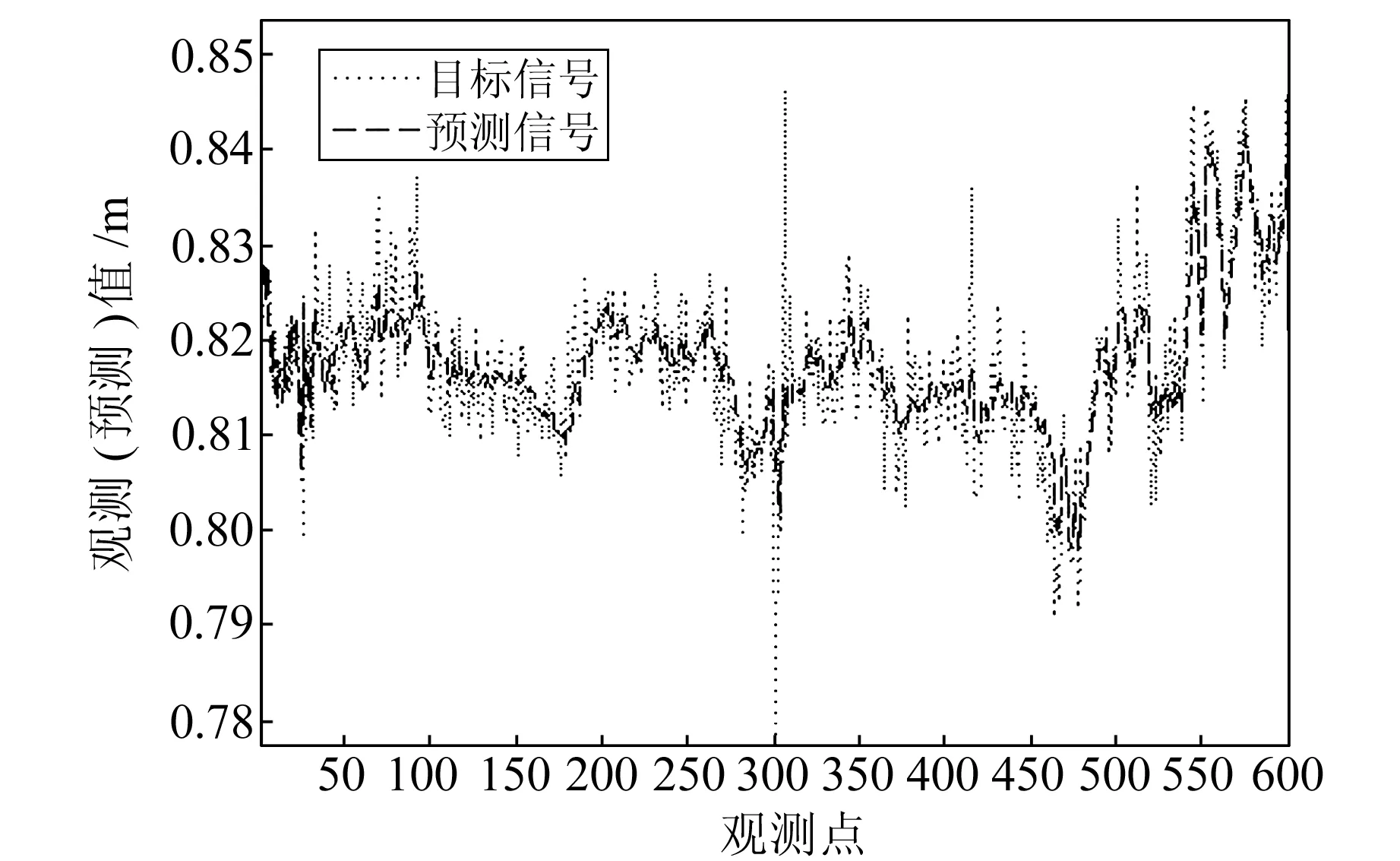
图3　在线ESN预测数据与实际数据对比Fig.3　Comparison between the predicted data by online-ESN and the actual data

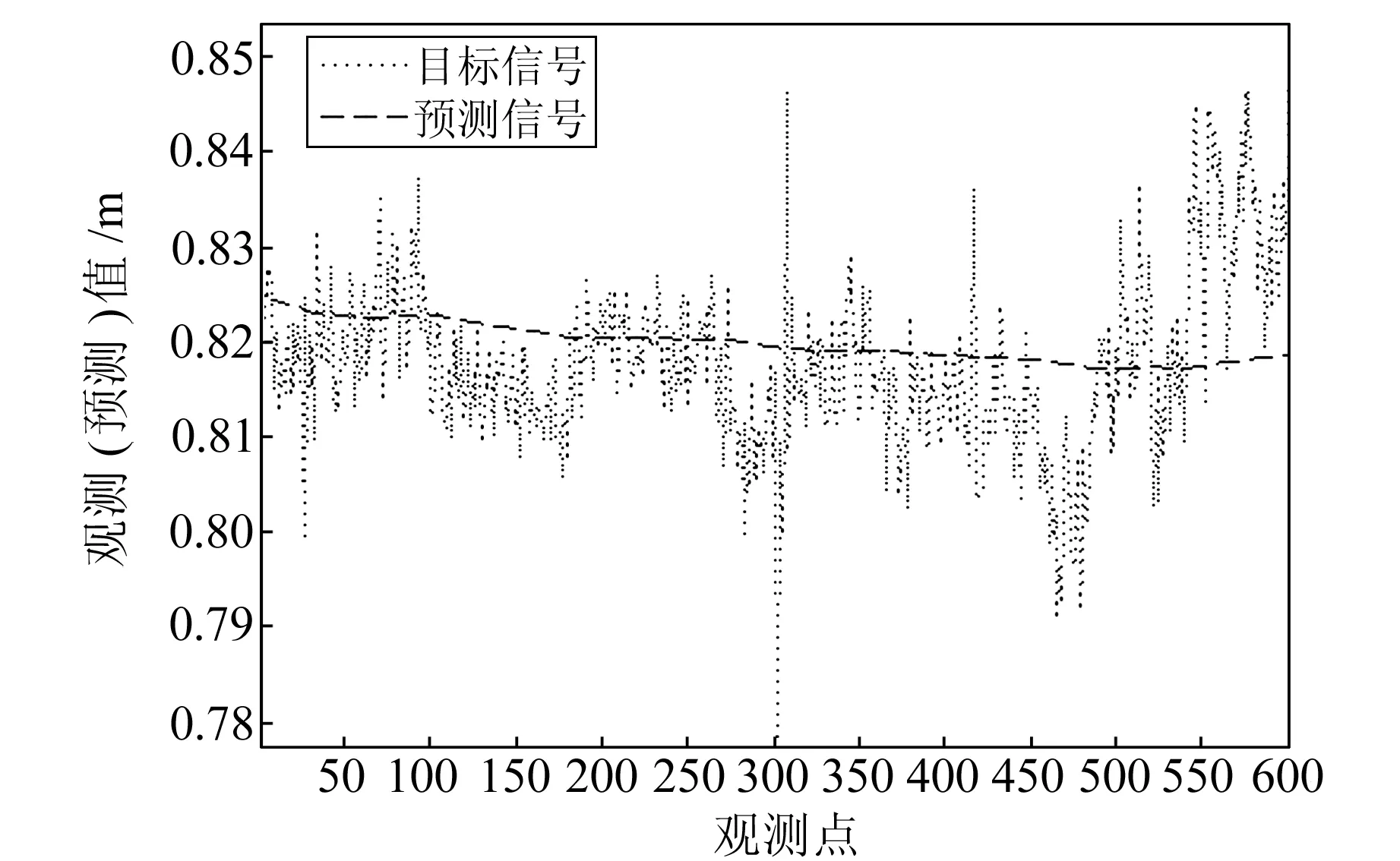
图4　Kalman滤波预测数据与实际数据对比Fig.4　Comparison between the predicted data by Kalman fliter and the actual data

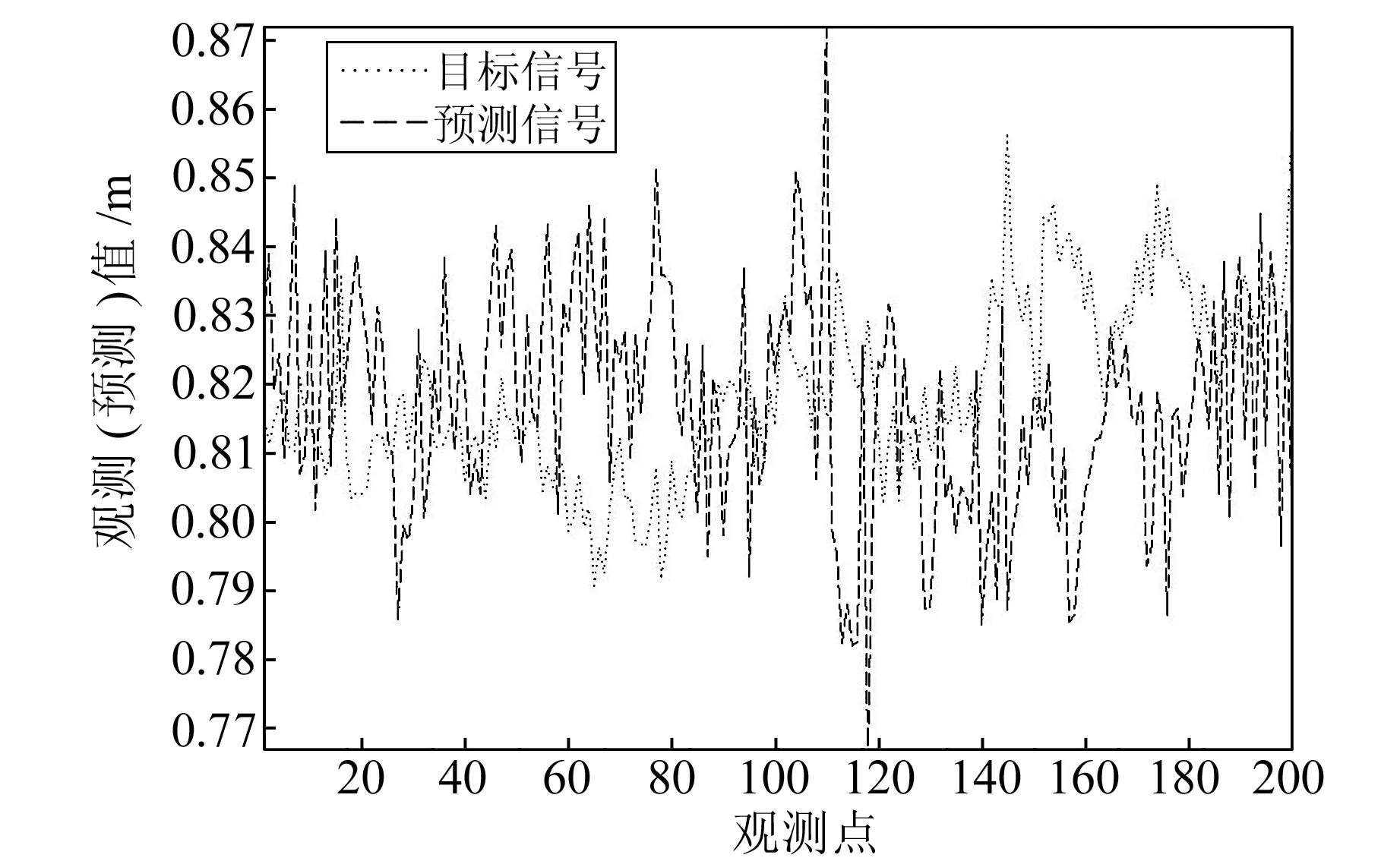
图5　BP网络预测数据与实际数据对比Fig.5　Comparison between the predicted data by BP and the actual data

计算3种算法对20 d数据的预测均方误差，结果见表1。从表1看出, 由于对数据作了预处理，使得该类型数据具有一定的平稳性，所以3种算法在预测此类型变形数据时效果都较好。然而，BP网络需要在预测前收集大量数据，在灵活性方面较差。在线ESN的预测精度几乎比Kalman滤波高一倍，且无需事先知道模型的状态转移矩阵和观测矩阵。

表1　3种算法20 d预测精度比较

3结语

本文将在线ESN用于沉降变形数据的预测，并以淮南市潘一东煤矿某月的数据进行实验。结果表明，采用在线ESN更加适合于不确定性很强并且变化范围有限的变形系统，其不需要记忆很多的训练样本，更具灵活性和便易性，预测精度与离线学习的BP网络相当。

参考文献

[1]盛守照，王道波，黄向华.限定记忆的前向神经网络在线学习算法研究[J]. 控制与决策，2005, 20(3)：304-307(Sheng Shouzhao，Wang Daobo，Huang Xianghua. Online Learning Algorithm for Feed Forward Neural Networks with Moving Range[J].Control and Decision,2005, 20(3)：304-307)

[2]朱玉，赵卿，梅艳.混沌免疫优化RBF网络在动态变形预测中的应用[J].大地测量与地球动力学,2012，32(5)：53-57(Zhu Yu，Zhao Qing，Mei Yan. Prediction of Dynamic Deformation Based on Chaotic Immune Optimization Algorithm RBF Nueral Network[J]. Journal of Geodesy and Geodynamics,2012，32(5)：53-57)

[3]潘国荣，谷川.GMDH神经网络算法在变形预测中的应用[J].大地测量与地球动力学，2008，28(3)：55-58(Pan Guorong,Gu Chuan. GMDH NN Algorithm and Its Application in Deformation Forecasting[J].Journal of Geodesy and Geodynamics,2008，28(3):55-58)

[4]彭祥国, 王坚, 孙丽红. BP网络最佳维数建模法在变形时序预测中的应用[J]. 大地测量与地球动力学, 2009, 29(6):113-117(Peng Xiangguo，Wang Jian,Sun Lihong. Application of Optimal Dimension Modeling for BP Network in Pridiction of Time Series of Derormation[J].Journal of Geodesy and Geodynamics， 2009， 29(6)：113-117)

[5]Jaeger H. The Echo State Approach to Analysing and Training Recurrent Neural Network[R].Fraunhofer，2001

[6]Jaeger H. Short Term Memory in Echo State Network[R]. Fraunhofer，2002

[7]韩敏，王亚楠. 基于Kalman 滤波的储备池多元时间序列在线预报器[J].自动化学报,2010, 36(1)：169-173(Han Min，Wang Ya’nan. Multivariate Time Series Online Predictor with Kalman Filter Trained Reservoir[J].Acta Automatica Sinica,2010, 36(1)：169-173)

[8]符拯，王书满，刘丙杰.自适应卡尔曼滤波的最新进展[J].战术导弹技术,2009(6)：62-66(Fu Zheng，Wang Shuman，Liu Bingjie. An Overview of the Development of Adaptive Kalman Filtering[J]. Tactical Missile Technology，2009(6)：62-66)

[9]涂克楠，高飞，黄芳伟.时间序列预测法在大坝变形监测数据处理中的应用[J].水科学与工程技术,2008(3)：65-67(Tu Ke’nan, Gao Fei, Huang Fangwei. The Application Time Series Forecasting Method in Data Processing of Dam Deformation Monitoring[J].Water sciences and Engineering Technology,2008(3)：65-67)

[10]张勇，田林亚，马丙浩，等.卡尔曼滤波在GPS 精密单点定位中的应用研究[J].测绘通报,2013(7)：8-11(Zhang Yong,Tian Linya,Ma Binghao,et al.Research on the Application of Kalman Filtering in GPS Precise Point Positioning[J].Bulletin of Surveying and Mapping,2013(7)：8-11)

[11]王新志，陈伟，祝明坤. 样本数据归一化方式对基于神经网络的GPS高程转换的影响[J].测绘科学,2013, 38(6):162-165(Wang Xinzhi,Chen Wei,Zhu Mingkun. Influence of Sample Data Normalization Ways on GPS Elevation Transforming Based on Neural Network[J]. Geomatics Science, 2013，38(6)：162-165)

Foundation support:National Natural Science Foundation of China, No.61572015.

About the first author:SHAN Yi, postgraduate, majors in pattern recognition and neural network, E-mail：15556530753@163.com.

Analysis and Prediction of Deformation Data Based on Online Echo State Network

SHANYi1YANGJianwei1WANGXinzhi2

1School of Mathematics and Statistics，Nanjing University of Information Science and Technology，219 Ningliu Road, Nanjing 210044, China 2School of Remote Sensing， Nanjing University of Information Science and Technology，219 Ningliu Road, Nanjing 210044, China

Abstract:A new kind of on-line predictor is constructed by combining Kalman filtering with the echo state network. The method of Kalman filtering is applied to the echo state network output weights training, directly on-line updating the network output weights, overcoming the defects in traditional recurrent neural network(RNN) which is needed to collect a large number of samples.The examples demonstrate the effectiveness of the proposed method.

Key words:on-line learning; observation of deformation data; echo state network; Kalman filtering

收稿日期：2015-06-25

第一作者简介：单毅，硕士生，主要研究方向为模式识别与神经网络，E-mail：15556530753@163.com。

DOI：10.14075/j.jgg.2016.07.013

文章编号：1671-5942(2016)07-0617-03

中图分类号：P258

文献标识码：A

项目来源：国家自然科学基金(61572015)。