基于微分形态学断面的机载LiDAR数据滤波新方法

孙　蒙　顾和和

1　中国矿业大学环境与测绘学院，徐州市大学路1号，221116

基于微分形态学断面的机载LiDAR数据滤波新方法

孙蒙1顾和和1

1中国矿业大学环境与测绘学院，徐州市大学路1号，221116

摘要：提出一种基于微分形态学断面的机载LiDAR点云数据滤波新方法。该方法由点云数据构建规则格网，去除粗差点；对构建的每一个格网进行多尺度分解，获取初始地面点及地物点；分别利用曲面逼近及微分形态学断面构建DTM(digital terrain model)，通过阈值函数判别二者之间的残差，确定最终地面点。使用国际摄影测量与遥感学会提供的测试数据进行实验，并与8种经典滤波算法比较分析，表明该方法能够有效去除地物点和保留地面点，并降低总误差。

关键词：微分形态学断面；多尺度分解；数学形态学；滤波；精度评定

LiDAR可低成本、快速、大范围、实时获取高精度三维点云[1]，被广泛应用到构建数字高程模(digital elevation model,DEM)及获取各种图像产品[2-3]。由于受建筑物、植被和车辆等地物的影响，原始三维点云中含有非地面点，为此需对其进行滤波处理[4]。经典滤波算法有基于内插[5-6]、坡度[7-8]和形态学的滤波[9]等。基于内插的滤波方法认定地球表面为连续变化的曲面，通过一个起始DEM逐步从备选点筛选并内插加密实现分类目的，易受初始DEM的影响且误差会随迭代过程积累。基于坡度的滤波方法需量测两点之间的高差或坡度，通过预设的坡度阈值完成分类，易受地形变化及阈值选取的影响，滤波方法自适应性不强。基于形态学的滤波方法仅考虑窗口内的地形特征，易受局部地形的影响，且滤波过程中参数需要用户根据不同地形设置，自适应性不强。针对数学形态学滤波算法存在的问题，本文提出一种基于微分形态学断面(differential morphological profiles, DMPs)的机载LiDAR数据滤波新方法。使用国际摄影测量与遥感学会(ISPRS)提供的样本数据进行实验表明，该算法可以得到较好的滤波结果并使总误差较小。

1DMPs滤波原理和步骤

为克服地形起伏的影响，考虑到滤波区域目标尺寸形状差异，本文在预估的粗糙近似曲面上基于微分形态学断面进行多尺度分解。算法主要流程分为点云格网化、DMPs构建和点云滤波3步(图1)。

图1　微分形态学断面滤波流程图Fig.1　The framework of the DMPs filter

1.1点云格网化

设原始LiDAR点云集合为L={li}，则预处理后构建的格网表示为E={gi}。其中E的范围由L的边界确定；gi不仅包含格网内所有的原始点云信息，同时特指该格网内最低点的三维坐标信息。规则格网化的步骤如下。

1)确定格网分辨率Rg。Rg取原始LiDAR点云密度DL的倒数，即

(1)

2)确定单元格值。若格网化后单元格内存在的原始最低点为p，则该单元格的值为p点高程值g[p]；对于空单元格，其值g[p*]由邻近的单元格内插得到。本文采用反距离加权法[10]，即

(2)

由于多路径效应及仪器误差的影响，原始点云中存在粗差点，本文通过构建格网剔除低位粗差点(远低于地面的点)。

1.2DMPs构建

通过多尺度格网分解方法对格网g中含有的特征进行映射分析，其决定了点云滤波后生成的DTM的精度。首先将预处理后获得的格网g分解为低频带g↓和高频带g↑，g↓通过高斯核函数G对格网g进行卷积运算得到，该卷积运算可剔除格网g中大部分的非地面特征；g↑为获取g↓后格网g的剩余部分，即

(3)

式中，*为卷积运算，G为高斯核函数。由于g↑为滤除大部分非地面特征的近似地面，接下来的处理主要是针对g↑。

设rωs(g↑)为对g↑进行数学形态学的开运算，ωs是大小为s的圆盘结构元素。通过一系列呈渐进变化的滤波窗口，采用形态学开运算粒度测试技术对g↑进行多尺度分解。这些滤波窗口集合为s={0,1,2,…,S}，其中S为所包含目标的最大尺寸。故格网g的微分形态学断面表示为[11]：

(4)

式中，i∈[1,I]，I为集合s的势减1。如图2所示，对于每一个特定点p，Δ(g↑)为g↑的分解，Δ(g↑)[p]为该处长度为I的响应矢量，该矢量包含与每一个rωsi有关的高差值。

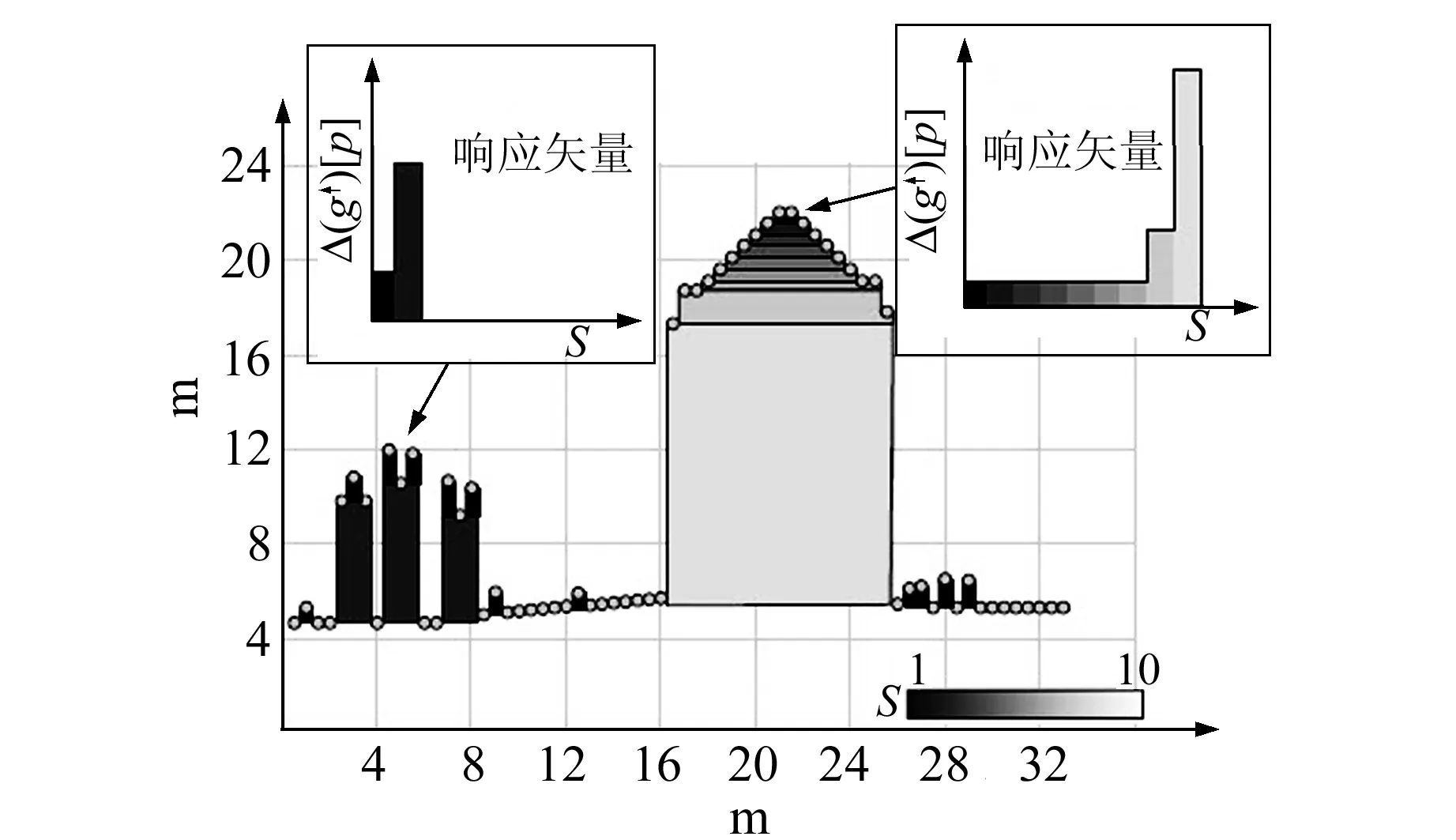
图2　格网分解过程Fig.2　Decomposition of a grid

对Δ(g↑)进行特征映射，可获得g′和g*。g′是表征每一点p处所获得的Δ(g↑)的最大相应函数；g*是在p点得到最大响应值时求取最小滤波窗口的函数。定义函数θws(g↑)用于求取p点处的g′和g*，即

(5)

式中，∨为上确界，∨为下确界。g′描述了目标特征与周边地形之间的高差，g*则是对目标特征大小的估计。

1.3点云滤波

尽管通过设置g′的阈值可以识别和移除不满足假设的目标，但是一些小块低矮地物会对g′的判别有影响，故应考虑将g*也作为判别准则。本文采用线性阈值函数T(g*)[p]，定义为：

(6)

式中，k和n为用户自定义常量，描述了特征尺寸与残差的相关系数，与地形环境及地物复杂程度有关。地面点集SG和非地面点集SNG表示为：

(7)

(8)

对于获取的地面点集SG，采用式(2)内插生成DTM。为此，可在阈值函数T(g*[p])基础上，采用外置形态学梯度阈值函数∂DTM,即∂DTM=δωi(DTM)-DTM。其中，δωi(DTM)为用最小尺寸的结构元素(如3×3)进行形态学膨胀运算得到的结果。则一系列地面点集LG可通过下式获取：

(9)

式中，dh(li)为原始点云L中某一点li与相应DTM之间的绝对高程差，b为用于定义DTM与地面点之间的最大高差。

2实验与结果分析

2.1实验数据

本文用来测试的数据为ISPRS第Ⅲ小组2003年采集的一组数据集。该数据集位于德国南部的Vaihingen/Enz和Stuttgart市中心，包含多种特征目标(植被、建筑物、道路、铁路、河流、桥梁、电力线、水面等)，由Optech公司的ALTM机载LiDAR测量系统获取，其首末次回波皆可用。数据集由15个样本组成，其中包含平均点间距为1～1.5 m的城区(samp11～42)及平均点间距为2～3.5 m的山区(samp51～71)。每个样本都由测试数据与参考数据2个部分组成，参考数据通过半自动滤波及结合影像的人工识别进行地面点与非地面点的精确区分。

2.2实验参数选取

本文方法需要用户自定义4个常量，而其中常量S一般指滤波区域内的最大地物尺寸，决定着算法的运行效率；常量b为高差阈值，与初始地面点生成的DTM精度有关；常量k、n的取值受地形环境的复杂程度影响，本文采取单一变量法，k与n在0～1之间呈线性递增取值，通过比较滤波后生成的DTM确定最优值。

2.3实验结果分析

通过C++编程实现该算法，并对这15个样本进行滤波处理。实验所用最优参数、滤波所用时间及结果见表1。可以看出，滤波过程所耗时间皆在0.3 s以内，算法每s可处理百余万点云，说明该算法运行效率高。由滤波结果中存在的Ⅱ类误差可以看出，无论在山区还是城区，其结果都能满足实际需求，证明该算法滤波自适应强。

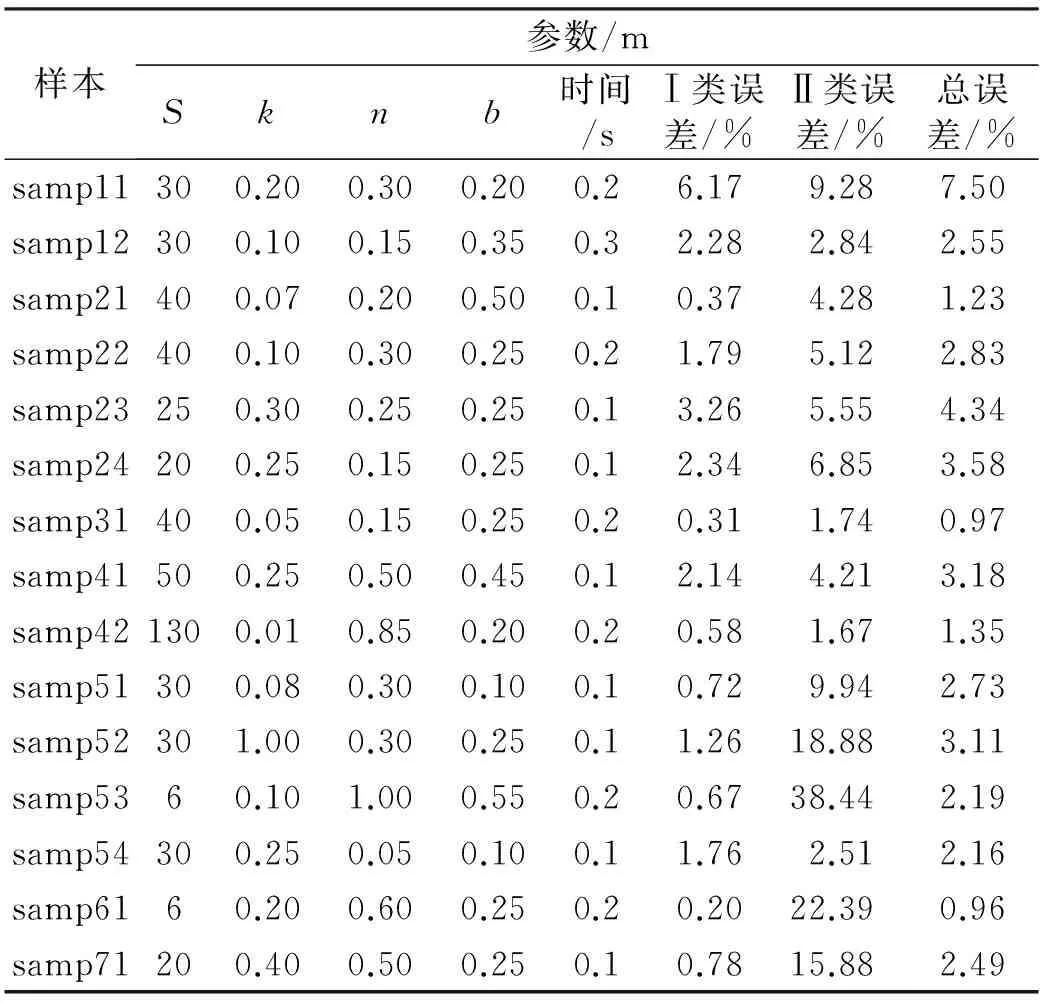
表1　实验参数值

2.3.1定性比较

通过表1，分别从城区和山区样本中选择总误差最大的样本samp11及内插生成的DTM平均误差最大的样本samp53进行定性比较，图3显示了每一个样本的原始DSM、滤波后DTM以及滤波后Ⅰ类和Ⅱ类误差的空间分布。从图3(a)可以看出，由于陡坡上建筑物多、目标复杂以及裸露梯田的存在，导致建筑多的地方滤波后Ⅰ类误差明显增大。Ⅱ类误差主要受低矮植被的影响(图3(c))。从图3(d)可以看出，由于存在粗糙狭窄的褶皱与陡崖，导致滤波后Ⅰ类误差主要分布在陡崖处及褶皱地带(图3(f))。

图3　样本滤波前后的DTM及Ⅰ类、Ⅱ类误差空间分布Fig.3　The DTM before and after filtering and type Ⅰ errors and type Ⅱ errors of samples

2.3.2定量分析

将15个样本经DMPs滤波后与ISPRS提供的8种经典滤波算法进行对比分析，结果如表2所示。表中黑色加粗字体即为每一行的最小值，表示相对应的滤波方法在该样本中滤波效果最好。通过表2可以看出，本文提出的算法在样本samp11、samp12、samp21、samp22、samp24、samp31、samp41、samp42、samp53、samp54、samp61及总平均误差上优于8种经典算法。因为以上这些样本区域内无复杂建筑物、地表连续变化，故通过DMPs构建生成的初始DTM精度高，能滤除大部分的非地面点，保证后续滤波精度。在样本samp11、samp41及samp53中虽然总误差比较小，但是由于非地面点数远小于地面点数，错分类的非地面点会使Ⅱ类误差明显增大。在剩余样本中本文算法滤波结果与最优滤波算法Axelsson结果相差不大。剩余的样本特征为复杂建筑物或低矮植被，如在样本samp51与samp52中，由于区域内低矮的植被点较多，根据生成的形态学梯度阈值函数进行判别时，结构元素内最低的植被点会被保留下来，使总误差及Ⅱ类误差增大。而Axelsson算法假设地形局部区域是平坦的，然后选择局部区域内的最低点作为种子点来构建初始稀疏三角网，并依据三角网内随机点距离三角形最近顶点的高度夹角和垂距来判断该点是否为地面点。如果是地面点，则加密TIN模型，依次迭代直到没有新的地面点为止。该算法比较适用于建筑物密集的城区以及地形不连续的区域，故在剩余样本中该方法的滤波结果较好。

表2　MHC与8种经典滤波算法总误差比较

3结语

本文借鉴微分形态学断面在遥感影像处理方面的应用，提出了一种新的形态学滤波策略。该方法对点云数据进行规则格网化、滤除粗差点；对构建的每一个格网进行多尺度分解，获取初始地面点及地物点；分别利用曲面逼近及微分形态学断面构建DTM，通过阈值函数判别二者之间的残差，确定最终地面点。该方法解决了数学形态学滤波算法中存在的两个问题:局部地形不连续对分类的影响以及坡度或高差阈值的人工选取。但是在建筑物复杂的城区以及低矮植被较多的区域，该方法不能很好地克服因形态学梯度误差引起的误分类。比较实验结果可知，该方法能快速有效地识别地面点和地物点，并且保留地形的细节信息，满足精度需求。

参考文献

[1]Yun J, Gao C X, Zhu S L, et al. High-Peak-Power,Single-Mode,Nanosecond Pulsed,All-Fiber Laser for High Resolution 3D Imaging LiDAR System[J]. Chinese Optics Letters, 2012, 10(12):39-41

[2]Lai X D,Han Z J. Hige Fidelity DEM Generation Based on LiDAR Data[J].Journal of Computers,2012,7(8):2 071-2 077

[3]范士俊，张爱武，胡少兴，等．基于随机森林的机载激光全波形点云数据分类方法[J].中国激光，2013，40(9)：216-222(Fan Shijun,Zhang Aiwu,Hu Shaoxing, et al. A Method of Classification for Aribone Full Waveform LiDAR Data Based on Random Forest[J].Chinese Journal of Lasers, 2013,40(9)：216-222)

[4]刘凯斯．机载激光LiDAR点云数据滤波和分类算法研究[D]．北京：首都师范大学， 2014(Liu Kaisi. The Research of Airborne Laser LiDAR Point Cloud Data Filtering and Classification Algorithm[D]. Beijing: Capital Normal University, 2014)

[5]Vosselman G. Slope Based Filtering of Laser Altimetry Data[J]. International Archives of Photogrammetry and Remote Sensing and Spatial Information Sciences, 2000,33(B3): 935-942

[6]Mongus D, Zalik B.Parameter-Free Ground Filtering of LiDAR Data for Automatic DTM Generation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012,67(1):1-12

[7]Filin S, Pfeifer N. Segmentation of Airborne Laser Scanning Data Using a Slope Adaptive Neighborhood[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006,60(2),71-80

[8]Tovari D,Pfeifer N. Segmentation Based Robust Interpolation a New Approach to Laser Data Filtering[J].International Archives of Photogrammetry and Remote Sensing and Spatial Information Sciences,2005,36(19),79-84

[9]罗伊萍,姜挺,龚志辉. 基于自适应和多尺度数学形态学的点云数据滤波方法[J]. 测绘科学技术学报,2009,26(6):426-429(Luo Yiping, Jiang Ting ,Gong Zhihui.An Adaptive and Muli-Scale Mathematic Morph-ological Filter for Point Cloud Data Filtering[J]. Journal of Geomatics Science and Technology,2009,26(6):426-429)

[10]Chaplot V, Darboux F, Bourennane H, et al. Accuracy of Interpolation Techniques for the Derivation of Digital Elevation Models in Relation to Landform Types and Data Density[J].Geomorphology,2006,77(1-2):126-141

[11]Pesaresi M, Benediktsson J A. A New Approach for the Morphological Segmentation of High-Resolution SatelliteImagery[J]. IEEE Transactions on Geoscience and Remote Sensing,2001, 39(2): 309-320

Foundation support:Commonweal Research Project on Land and Resources,No.201111013; Priority Academic Program Development of Jiangsu Higher Education Institutions,No.SZBF2011-6-B35.

About the first author:SUN Meng, postgraduate, majors in airborne LiDAR point cloud data processing，E-mail：519282720@qq.com.

A New Filtering Method for Aribone LiDAR Data Based on Differential Morphological Profiles

SUNMeng1GUHehe1

1School of Environment Science and Spatial Informatics, China University of Mining and Technology,1 Daxue Road, Xuzhou 221116, China

Abstract:This paper proposes a new filtering method for LiDAR Data. The proposed approach constructs the connectivity of a grid over the LiDAR point-cloud in order to perform multi-scale data decomposition. This is realized by forming a top-hat scale-space using differential morphological profiles (DMPs) on points’ residuals from the approximated surface. The International Society for Photogrammetry and Remote Sensing (ISPRS) reference dataset is used to test the method. The experimental results show that the proposed method can effectively remove non-ground points, keep the ground points, and is effective at minimizing total error rates.

Key words:differential morphological profiles；multi-scale data decomposition；mathematical morphology；filtering；accuracy assessment

收稿日期：2015-07-08

第一作者简介：孙蒙，硕士生，主要研究方向为机载LiDAR点云数据处理，E-mail：519282720@qq.com。 通讯作者：顾和和，教授，主要研究方向为测量数据处理、地籍测量，E-mail：guhh@263.net。

DOI：10.14075/j.jgg.2016.07.007

文章编号：1671-5942(2016)07-0591-04

中图分类号：P237

文献标识码：A

Corresponding author:GU Hehe, professor, majors in surveying data processing and cadastral surveying, E-mail：guhh@263.net.

项目来源：国土资源公益性行业科研专项(201111013)；江苏省高校优势学科建设工程(SZBF2011-6-B35)。