数学中的对称美
●龚利娜
数学中的对称美
●龚利娜
对称美是美的一种重要形式,一种特殊形式,它能给予人们一种圆满、均匀、协调和平衡的美感,让每一个人看到它,心情都会变得轻松、舒坦起来。下面,笔者就结合自己的教学实践,从四个方面来阐述数学中的对称美。
一、几何图形的对称美
几何图形中,有许多的图案都具有对称性,具有对称美,其中,圆形就是一个很好的例子。我们都知道,圆形就是一个轴对称图形,有无数条对称轴,任意沿着它的一条对称轴折一折,两边分成的图形就会完全重合在一起。另外,圆形给人的感觉就是一个非常漂亮的物体,因为它有很完美的闭合曲线,所以,世界上许多的经典建筑,都有圆形的影子,正如毕达哥拉斯所说:“一切平面图形中最美的是圆形。”
再比如,有些对称图形经过动手操作后,可以变成更漂亮的图形。下面的图1是一个正三角形,笔者让学生把该三角形的每条边平均三等分,以每条边中间的三分之一为边向外再作一个小正三角形,可得图2的六角星形,它也是一个对称图形;然后,让学生在该六角星形的每条边上用同样的办法向外再作一个更小的正三角形,可得图3的雪花形多边形,也就是数学家科赫雪花的科赫曲线……以此步骤继续操作可得到一系列边数越来越多的多边形。它们虽然面积不大,但是无论你怎么去重复操作,无论怎么变化,最后呈现的图形还是对称图形,这些图形变得越来越好看,越来越有规律,这就体现了对称图形的神秘之处。
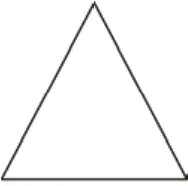
图1

图2

图3
二、数与式的对称美
对称美不仅表现在几何图形中,数与式子也具有对称性,主要表现在一些运算中。
如在进行珠心算加法练习的时候,笔者先让学生在算盘上拨入对称数112211,先加112211,算盘上得到了224422,再让学生加112211,算盘上的结果是336633,这样连续操作11次,算盘上的结果却变成了另外的一个数字:1234321,它是一个对称数,这让学生大吃一惊。这样教学,既调动了课堂的气氛,又激发了学生学习珠心算的兴趣。课后,有学生指出:“以前,我对算盘一点也不感兴趣,可今天通过老师的教学,我感觉算盘太奇妙了,现在,我不仅愿意学珠心算,而且更愿意学习数学了。”
比如,以1为例,将它进行乘法计算,就会出现一些对称的结果:
1×1=1
11×11=121
111×111=12321
1111×1111=1234321
11111×11111=123454321
……
这样的乘法计算,让学生一眼就能看出其中的规律,也就能很快写出所要得到的答案。通过这样的教学,学生不仅获得了有关的数学知识,而且受到了美的熏陶。
三、解题过程的对称美
几何图形不仅具有对称美,在解题的过程中,巧妙地运用对称性质进行适当增补,有利于发现解决问题的突破口,训练解题的技巧,简化解题过程。
如要求图4阴影部分的面积,此题按照常规的方法去求,阴影部分的面积应该等于扇形面积减去三角形的面积。在教学的过程中,学生可以发现三角形的面积一时无法去求,他们无法下手,这就使得解题陷入了困境。

图4
这个时候,教师就要及时点拨学生,让他们从对称的角度去思考,也就是作一个对称图形,形成图5,再做适当的提醒,学生就会发现:图5中阴影部分的面积等于圆面积的四分之一减去等腰直角三角形的面积,而图4中阴影部分的面积等于图5中阴影部分面积的一半。这种解法学生即容易理解又能够牢记,都感叹此种解法的精妙。

图5
(作者单位:鄂州市梁子湖区徐连小学)
实习编辑孙爱蓉
责任编辑刘玉琴

