车辆主动悬架的最优控制研究

米磊，李国峰，于翠

（华晨汽车工程研究院，辽宁 沈阳 110141）



车辆主动悬架的最优控制研究

米磊，李国峰，于翠

（华晨汽车工程研究院，辽宁 沈阳 110141）

摘 要：在建立主动悬架二自由度动力学模型的基础上，运用最优控制理论求解目标性能函数并进行最优控制器的设计，利用Matlab/Simulink进行了模型建立与仿真分析。仿真结果表明，运用最优控制的主动悬架各项性能对比被动悬架均得到了明显改善。

关键词：主动悬架；动力学模型；最优控制

10.16638/j.cnki.1671-7988.2016.04.011

CLC NO.: U462.1Document Code: AArticle ID: 1671-7988(2016)04-29-03

前言

被动悬架系统主要由弹性元件和被动阻尼元件组成，系统的刚度和阻尼固定不变[1]。然而，车辆在实际的行驶过程中，受载荷、行驶速度以及路面不平度变化等因素的影响，悬架系统的参数偏离了最初设计的折衷方案而不再表现为最优。因此，被动悬架难以满足各工况下不同的性能要求。

主动悬架主要由控制系统和替代了弹性元件和被动阻尼元件的执行机构组成。相比于被动悬架，主动悬架能够根据当前车辆的运行状态及路面输入激励的变化，实时地将主动控制力作用于悬挂质量与非悬挂质量之间，使系统性能始终处于最佳。描述悬架系统性能的指标包括车身加速度、轮胎动位移以及悬架动挠度，其中前两者分别反映了车辆的乘坐舒适性和操作稳定性。同时，应使悬架系统达到目标性能所需的控制能量最小。因此，对于主动悬架的控制，可将这四个性能指标加权后的二次函数作为控制策略的目标函数，采用最优控制算法来综合考虑悬架系统中的各种因素，从而达到对系统性能的全面改善。

1、车辆悬架动力学模型

通常车辆行驶的左右路面统计特性近似一致，且认为在纵向轴线上，车身只进行小幅度的摆动，忽略侧倾和横摆运动。本文为了简化控制模型，突出研究问题的主要方面，将主动悬架系统简化为图1所示的二自由度1/4车模型。

由图1得悬架系统的动力学方程：

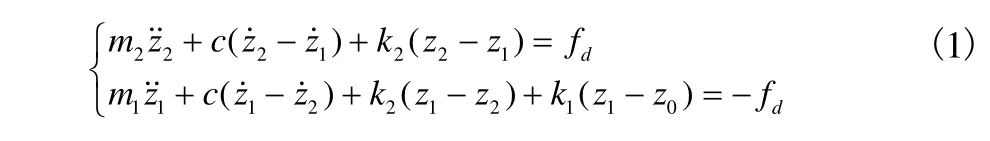
式中，m2、m1分别为悬挂质量和非悬挂质量；z2、z1分别为其对应的位移；k2为悬架刚度系数；k1为轮胎径向刚度系数；c为悬架线性阻尼系数；fd为主动控制力；z0为随机路面激励。

图1　二自由度主动悬架模型

2、最优控制器的设计

将最优控制应用于主动悬架系统，满足车辆行驶平顺性和操纵稳定性的要求。此外，从实现控制的角度，应使所需的控制能量较小，因此悬架的性能指标可具体写为[2]：

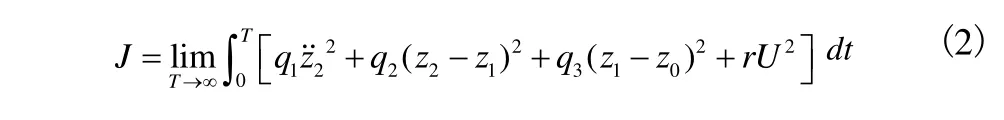
其中，q1，q2，q3分别为车身加速度、悬架动挠度以及轮胎动位移的加权系数，r为约束系数。当其中某个性能指标的分量较为重要时，可以将此分量的权系数增大；若此分量对研究的问题无关紧要时，则可将其权系数设为零。因此，根据研究的侧重点合理的选取加权矩阵是尤为重要的，加权系数的不同致使系统的性能也会完全不同。本节选取加权系数矩阵Q的原则为：在满足车身垂向加速度最小的前提下，同时能够保证悬架工作在合理的行程范围及车轮与路面保持良好的附着。

将式（2）转换为标准二次型的形式：

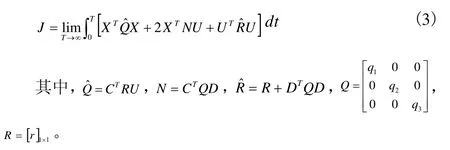
由最优控制理论可知，若控制作用：

则性能指标J最小，其中K为下列黎卡提方程的解：

根据任意时刻的状态反馈变量X(t)，可得出t时刻的最优控制力u(t) 。

根据图1建立主动悬架模型，选取状态变量X =

由状态方程：

得到系统矩阵A、控制矩阵B、输出矩阵C及传递矩阵D分别为：

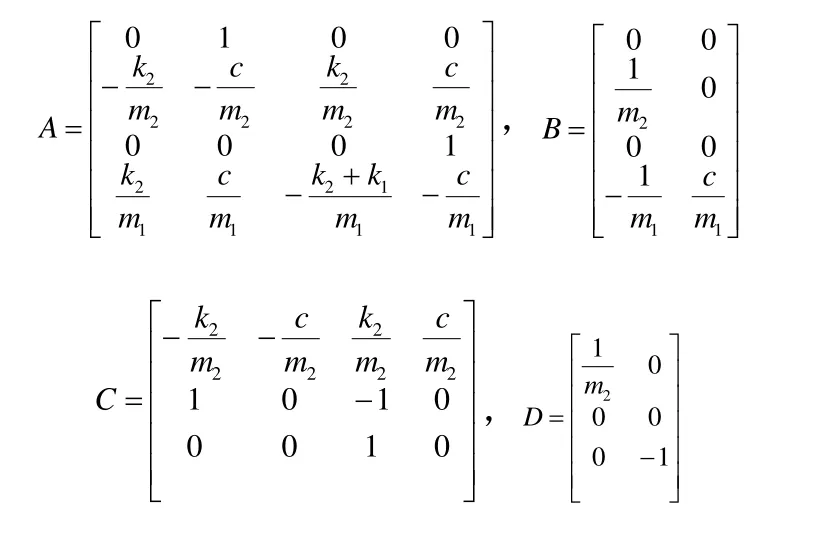
3、仿真分析

3.1 时域仿真分析

车轮受到路面激励[3]可以用微分方程表示为：

式中，f0为路面输入的下截止频率；G0为路面不平度系数；v为车速；w(t)为输入白噪声。

主动悬架系统的仿真参数如表1所示。同时，调用Matlab软件中的LQR函数[K,S,E] =LQR(A,B,Qˆ,N,Rˆ)完成最优控制器的设计，其中K为最优控制反馈增益矩阵，S为黎卡提方程的解，E为系统闭环特征根，求得最优反馈增益矩阵K=[2045-267452-2542925166]。

表1　主动悬架仿真参数表

为更好地分析基于最优控制的主动悬架的控制效果，将其与被动悬架进行比较。图3为车身垂向加速度、悬架动挠度以及轮胎动载荷的仿真结果对比，根据图可知，基于最优控制的主动悬架相比于被动悬架各项性能均有明显的改善。表2为不同性能指标相对应的均方根值。由表2可知基于最优控制的主动悬架的车身垂向加速度较被动悬架下降了20.72%，悬架动挠度下降18.11%，轮胎动载荷下降了10.14%，有效地提高了车辆的乘坐舒适性和操纵稳定性。

图2　系统的Simulink仿真模型图

图3　仿真结果

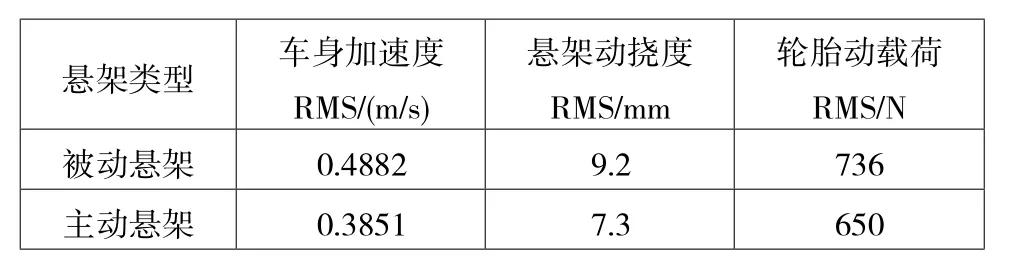
表2　不同悬架系统性能指标均方根值的对比分析

3.2 频域仿真分析

影响车辆行驶过程中平顺性和操纵稳定性的几个主要共振频段为[4]：（1）车身共振频率一般在1~2Hz之间；（2）人体的主要共振频率一般在4~8Hz之间；（3）轮胎跳动频率分布在8~18Hz之间。将评价悬架系统性能的关键指标垂向振动加速度的功率谱密度进行低频放大（20Hz），如图4所示，从图中可以看出，在人体垂向较为敏感（4~8Hz）的低频段，相比于被动悬架，基于最优控制的主动悬架更能够有效地抑制垂向加速度的波动，改善了乘坐的舒适性。

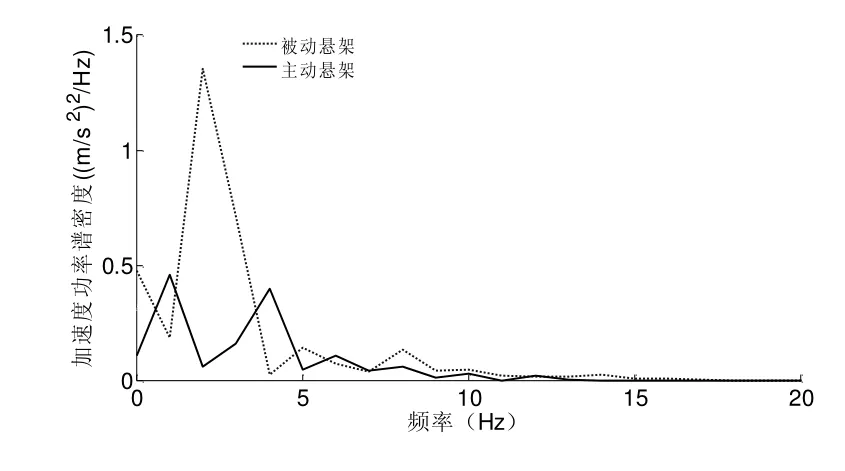
图4　车身加速度功率谱密度低频放大图

4、结论

（1）仿真结果表明：在主动悬架的设计中,采用最优控制理论来设计控制器可有效的改善车辆悬架系统的性能。

（2）在悬架系统性能的评价方面加入了特定频率段内车身加速度的功率谱密度分析，使仿真结果更具说服力。

参考文献

[1] 臧杰,阎岩.汽车构造(下册)[M].北京:机械工业出版社,2011, 2:127-133.

[2] 兰波,俞凡,刘娇蛟.主动悬架LQG控制器的设计[J].系统仿真学报,2003,15(1):138-140.

[3] 余志生.汽车理论(第3版)[M].北京机械工业出版社, 2000, 10:170-213.

[4] 俞凡,林逸.汽车系统动力学[M].北京:机械工业出版社,2005: 78-79.

中图分类号：U462.1

文献标识码：A

文章编号：1671-7988(2016)04-29-03

作者简介：米磊, 就职于华晨汽车工程研究院。

Research on optimal control of active suspension

Mi Lei, Li Guofeng, Yu Cui
( Brilliance Auto Engineering Research Institute, Liaoning Shenyang 110141 )

Abstract:Based on the two freedom dynamic model of active suspension, an optimal controller was designed by utilizing the method of optimal control theory for solving the objective performance function. The simulation analysis was carried out in the Matlab/simulink. The results of simulation showed that the vibration reduction effect of active suspension was obviously improved compared with the passive suspension.

Keywords:active suspension; dynamic model; optimal control