用于水泥熟料fCaO预测的多核最小二乘支持向量机模型

赵朋程，刘彬，高伟，赵志彪，王美琪（燕山大学信息科学与工程学院，河北 秦皇岛 066004；河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004；燕山大学电气工程学院，河北 秦皇岛 066004）



用于水泥熟料fCaO预测的多核最小二乘支持向量机模型

赵朋程1,2，刘彬1,2，高伟3，赵志彪1,2，王美琪1,2
（1燕山大学信息科学与工程学院，河北 秦皇岛 066004；2河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004；3燕山大学电气工程学院，河北 秦皇岛 066004）

摘要：针对水泥熟料游离氧化钙（fCaO）含量预测模型辨识的问题，考虑到单一核函数无法显著提高模型精度，采用多项式核函数、指数径向基核函数和高斯径向基核函数组合构建等价核的方法，建立了多核最小二乘支持向量机水泥熟料fCaO预测模型。同时，利用改进的粒子群优化算法对多核最小二乘支持向量机模型的6个待确定参数进行迭代寻优，避免了模型参数人工选取的盲目性。最后将基于改进粒子群的多核最小二乘支持向量机模型应用于熟料fCaO含量的实例仿真。结果表明，建立的水泥熟料fCaO含量预测模型精度高、泛化能力强。

关键词：多核学习；最小二乘支持向量机；模型；优化；算法；随机扰动

2015-10-21收到初稿，2016-03-01收到修改稿。

联系人：刘彬。第一作者：赵朋程（1990—），男，博士研究生。

Received date: 2015-10-21.

Foundation item: supported by the Natural Science Foundation of Hebei Province (F2016203354).

引　言

在水泥生产过程中，水泥熟料游离氧化钙（free calcium oxide in cement clinker，fCaO）是熟料质量的一项重要指标[1-2]，其含量的高低直接影响水泥的安定性以及生产能耗。目前，国外部分水泥生产企业使用在线分析仪测量水泥熟料fCaO含量，但设备维护成本较大，并且测量结果的准确性受到现场烟尘和工况的影响。国内大部分水泥生产企业的熟料fCaO值仍需每隔1～2 h现场取样离线化验得到，由于生料加工成熟料过程具有较大延时，离线获得的测量结果对于烧成系统的生产指导具有一定滞后性[3]。随着模型辨识技术的兴起，水泥熟料fCaO含量预测模型辨识方法的研究成为一个重要课题。

由于神经网络训练遵循经验最小化原则[4]，存在过拟合现象，并且网络训练复杂度随着样本数目的增加而增加。因此，Vapnik[5]基于统计理论提出了支持向量机（support vector machine，SVM）方法，但SVM的训练需要求解二次规划问题，影响了SVM的求解速度。Suykens等[6-7]提出了最小二乘支持向量机（least square support vector machine，LSSVM）的方法，利用最小二乘的方法将SVM的学习转化为求解线性方程组问题。近来，LSSVM及其改进形式被用于建立回归模型中[8-11]。但是，单一核函数LSSVM方法无法显著提高所建模型的精度，并且非线性学习能力有限。因此，文献[12-13]提出了多核学习的思想，为解决单一核函数对模型精度影响的问题提供了解决方向；文献[14-15]将多核学习的思想分别用于支持向量机和极端学习机中，提高了模型的精度，然而文献中模型的精度仍依赖于核参数的人工选取。为了避免模型参数的选取对模型精度的影响，粒子群(particle swarm optimization，PSO)算法被应用到模型参数寻优过程中[16-18]。

为了降低单一核函数及其参数选择对SVM建模精度的影响，本文首先结合不同核函数性质选取3种核函数构建等价核，用构建的等价核代替传统单一核函数，建立多核最小二乘支持向量机（multiple kernel least square support vector machine，MKLSSVM）模型；然后针对PSO算法搜索精度低、全局搜索能力差的缺点进行改进，提出一种带随机扰动的混沌粒子群（random perturbed chaos particle swarm optimization，RPCPSO）算法，并给出了RPCPSO算法优化MKLSSVM模型参数的步骤；最后将建立的MKLSSVM模型应用于水泥熟料fCaO含量预测建模中进行仿真实验。

1　多核最小二乘支持向量机

1.1MKLSSVM建模

MKLSSVM的核函数是通过G个不同类型的核函数线性加权组合得到的。假设训练样本数据集为，其中，N为训练样本数；xi∈ RN为输入矢量，RN为输入空间；yi∈ R为相应的期望输出，R为实数集，i=1,2, L ,N 。RN通过非线性函数ϕ( xi)被映射到高维特征空间Z，高维特征空间采用式（1）来估计未知非线性函数。

式中，wk∈Z 为ϕk(⋅)的权值，λk≥0为第k个核函数的系数，k=1,2, L ,G，b∈R为常值偏差矩阵。

根据结构风险最小化原则，将求解式（1）转化为求解如下最小值优化问题，其目标函数为

上述目标函数满足约束条件

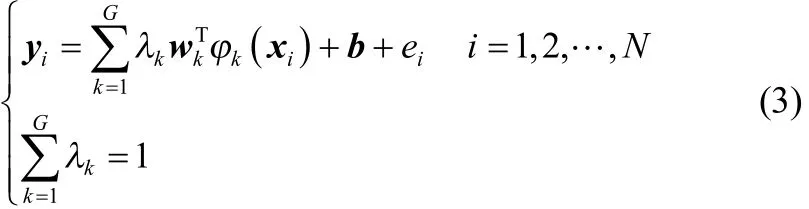
式（2）中正则化系数γ代表模型泛化能力及精度间的匹配参数，ei为第i个数据实际输出和期望输出间的误差。

采用Lagrange乘子法建立式（2）Lagrange函数

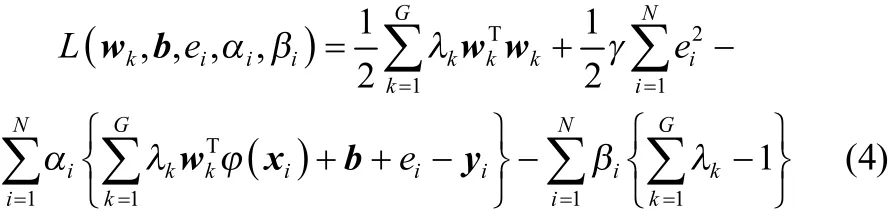
式中，αi∈ R和βi∈ R为Lagrange因子。

分别求取式（4）关于各变量的偏微分

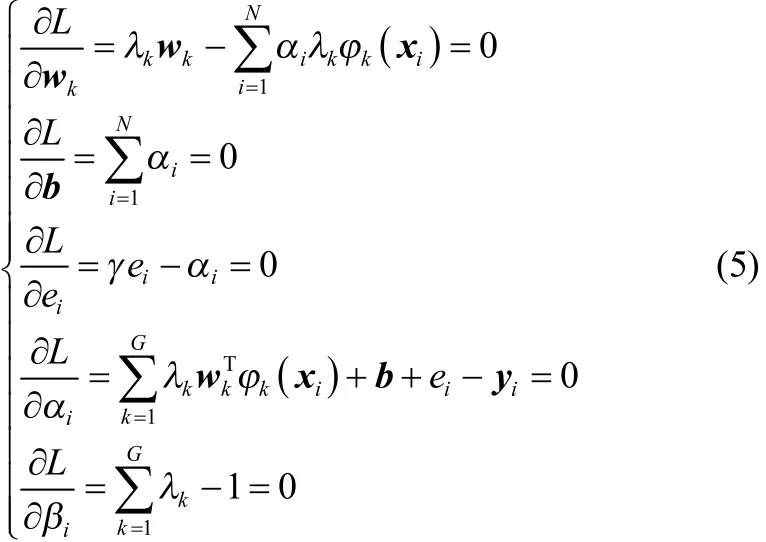
因此，消去变量wk、ei和iβ，得yi表达式为

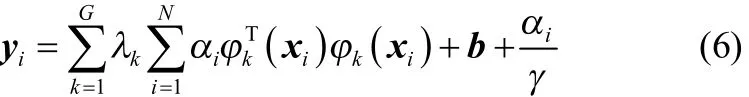
式（6）矩阵表达式为

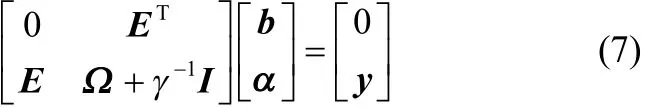
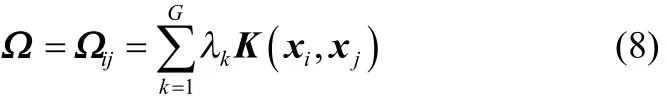
因此，将式（5）中wk表达式代入式（1），化简得到MKLSSVM对偶空间的表达式为

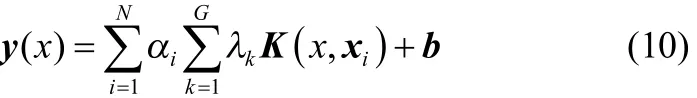
另，由于MKLSSVM的非线性映射能力是由核函数决定的[19]，因此选取合适的核函数将提高所建立模型的精度和泛化能力。

1.2核函数选取及待优化参数确定

在综合常用核函数特性并权衡模型精度与计算复杂度的基础上，选用三阶多项式、指数型径向基和高斯径向基3种核函数进行加权组合，构建等价核。三阶多项式核函数常用来表示非线性特征映射，C为其参数；指数型径向基核函数应用于离散回归问题时可产生线性分段解，参数σ′为其核宽度；高斯径向基核函数常用来表示非线性特性，参数σ为其核宽度。因此，用于MKLSSVM中的等价核函数可表示为

式中，1λ、2λ、3λ分别为其对应核函数系数，表示各个核函数所占比重。

根据式（3）的约束条件知λ3=1− λ1− λ2，另将所选3种核函数表达式代入式（10），MKLSSVM对偶空间的可表示为

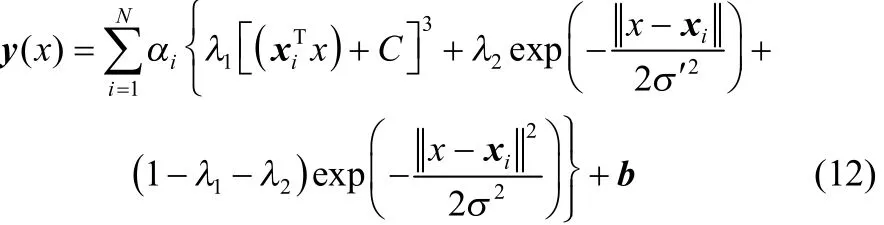
参数b及α是关于γ、C、σ′、σ、λ的参量，由式（9）求解得出。因此，上述包含3种核函数的MKLSSVM精度受到参数γ、1λ、2λ、C、σ′以及σ共计6个参数的影响。为避免人工选择参数的盲目性，本文利用带随机扰动的混沌粒子群算法对MKLSSVM待确定参数进行迭代寻优。

2　基于RPCPSO算法的MKLSSVM参数寻优

2.1RPCPSO算法建立

针对传统PSO算法收敛速度慢、全局寻优能力差以及搜索精度低的缺点，提出采用混沌映射保持粒子种群多样性，并且当寻优过程后期出现“聚集”现象时，在粒子速度更新公式加随机扰动的方法，既增加了粒子发现更优解的概率，又避免了算法后期陷入局部最优解，增加了搜索精度。

在RPCPSO算法中，假设搜索空间为D维，粒子个数为M，每个粒子被视为搜索空间中一点，并以一定速度飞行，则为粒子当前位置，为粒子当前速度，个体极值为，种群全局极值为。首先根据混沌序列初始化xi，先随机产生一个各分量在[0,1]之间的D维向量，由任意初值z1∈ [0,1]根据式（13）所示的Logistic混沌系统经过M−1次迭代产生一个混沌序列。

式中，i=1,2,L ,M− 1，取µ=4时，式（13）所示的系统处于完全混沌状态。

将各个分量根据式（14）载波到待优化变量的取值范围，得到RPCPSO算法的初始位置。

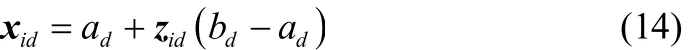
式中，i=1,2, L ,M ，d=1,2, L ,D ，xid∈(ad, bd)，ad和bd为待优化变量的取值范围。

当寻优过程后期出现“聚集”现象时，在粒子的速度更新公式中对个体极值iP和全局极值Pg加随机扰动，使所有粒子分散飞向不同的新的位置，经历新的搜索路径，增加粒子发现更优解的概率。以进化代数作为扰动的触发条件，设定随机扰动触发条件为Lt。

当进化代数l＜ Lt时，RPCPSO算法按照式（15）和式（16）更新粒子速度和位置。

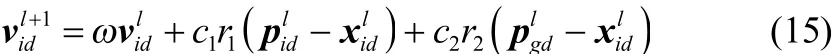
式中，l表示当前迭代次数，ω称为惯性权重，c1和c2为学习因子，1r和r2为分布于[0,1]之间的随机数。

当进化代数l≥ Lt时，RPCPSO就分别按照式（17）和式（18）更新速度和位置

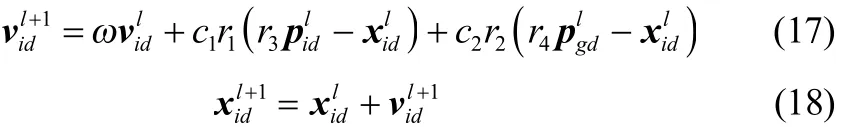
式中，r3和r4是在[α , β ]间的随机数，[α , β ]⊆ [0,1]为用户根据具体问题设置的随机扰动范围。

2.2RPCPSO优化MKLSSVM参数

采用RPCPSO算法对MKLSSVM模型待确定参数进行迭代寻优，避免模型参数选择的盲目性，减少其对建模精度的影响。根据式(12)可将MKLSSVM建模过程的寻优问题表示为

下面结合寻优问题式（19）给出RPCPSO算法优化MKLSSVM参数寻优步骤。

（1）初始化算法参数：维数D、粒子总数M、学习因子c1和c2、惯性权重ωmax、ωmin、最大迭代次数lmax、随机扰动触发迭代次数Lt等。

（2）根据混沌序列初始化粒子群位置，随机初始化粒子速度。

（3）MKLSSVM模型辨识，计算每个粒子的适应度值Fit，全局极值点pg和个体极值点pi为

（4）检查是否满足结束条件：l≥ lmax，如果满足则跳转到步骤（10），否则运行步骤（5）。

（5）由式（21）计算惯性权重，判断l＞ Lt是否成立，否则跳转至步骤（6）；是则跳转至步骤（7）。

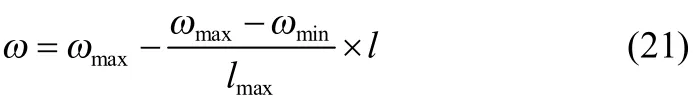
（8）计算混沌变量每一个可行解的适应度值Fit，并根据以下规则更新粒子全局极值点pg和个体极值点pi：若Fit(xi)＜ Fit( pi)，则pi= xi，否则pi不变；若Fit(pi)＜ Fit( pg)，则pg= pi，否则pg不变。

（9）迭代次数加1，跳转到步骤（4）。

（10）输出全局最优位置pg，pg为待寻优参数γ，C，σ′，σ，1λ，2λ组成的向量。

（11）采用已优化的参数γ，C，σ′，σ，1λ，2λ建立MKLSSVM模型，算法结束。

3　仿真分析

3.1RPCPSO算法验证

为了验证所提出的RPCPSO算法的有效性，选取Sphere(f1)、Ackley(f2)和Rastrigin(f3)3个常用Benchmark函数[20]进行算法性能测试，并将其与CPSO[21]、QPSO[22]以及PSO 3种算法进行对比。相关参数的设置情况为：Benchmark函数的维数D分别设置为10和20，其搜索范围和表达式如表1所示；CPSO和QPSO算法除了种群规模和最大迭代次数，其他参数设置同原文献；PSO中惯性权重设为0.9；RPCPSO中惯性权重ωmax= 0.9、ωmin= 0.2，随机扰动触发的迭代次数Lt设为800；种群规模M依次为50、100，最大迭代次数lmax均设置为2000。为了消除随机性的影响，每个算法均独立重复运行50次，其最优适应度函数平均值（mean fitness function value，MFFV）以及达到指定寻优精度所需的迭代次数平均值（mean iterations requested，MIR）分别如表2和表3所示。

表1　标准Benchmark测试函数Table 1　Benchmark test functions

由表2中MFFV数据比较可知，对于不同维度的测试函数，RPCPSO算法寻优精度均高于对比算法。比较表3中MIR数据可知，在函数f1和f2维数为10时，RPCPSO收敛速度不如QPSO算法；其他情况下，RPCPSO算法收敛速度均优于对比算法。因此，RPCPSO算法在求解高维复杂优化问题时具有较高的搜索精度以及较快的收敛速度。

表2　对3种Benchmark函数寻优结果的MFFVTable 2　MFFV of optimization result on three Benchmark functions

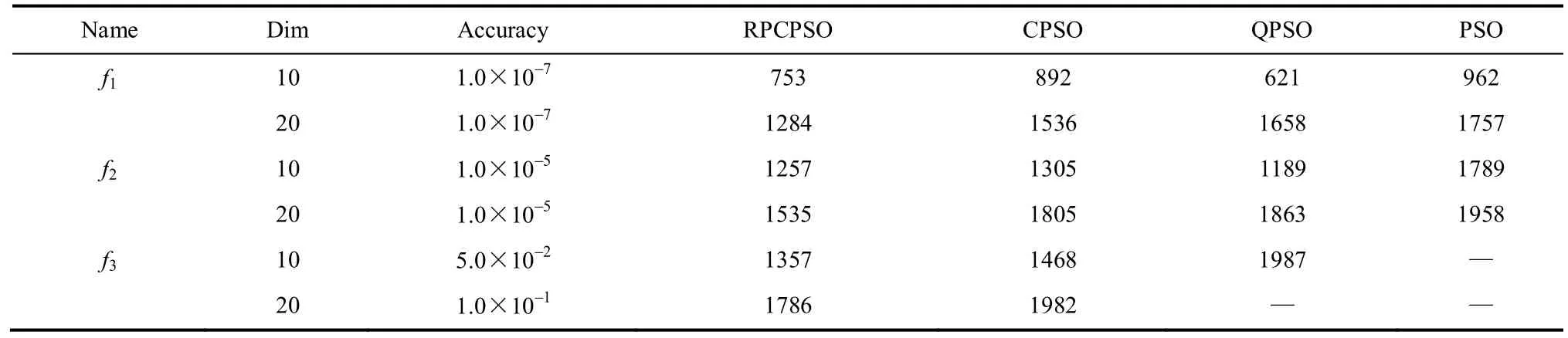
表3　对3种Benchmark函数寻优结果的MIRTable 3　MIR of optimization result on three Benchmark functions

3.2应用实例

由水泥生产机理可知，熟料fCaO含量高低主c1= c2= 2、惯性权重ωmax= 0.9、ωmin= 0.2、最大迭代次数lmax= 85、随机扰动触发迭代次数Lt=50。

LSSVM和MKLSSVM的模型参数在式(19)的约束范围内人工选取确定；PSO-MKLSSVM和要取决于生料的组成成分和生料的煅烧情况。在新型干法水泥生产工艺中，生料是经过成分配比、粉磨和均化后再进入煅烧系统，生料的组成成分相对稳定。因此，本应用实例建立的水泥熟料fCaO含量预测模型输入变量不考虑生料的组成成分的变化，只选取反映生料煅烧情况的相关变量作为模型的输入，包括分解炉出口温度、烟室NOx含量、窑主机电流、烟室温度和二次风温，选取水泥熟料fCaO含量化验室测量值作为模型输出。

从某水泥厂生产线DCS系统和化验室历史记录中共获得样本数据165组，随机选择其中的100组数据作为训练样本，其余的65组数据作为测试样本。为对比验证本文提出建模方法的有效性，分别采用LSSVM、MKLSSVM、PSO-MKLSSVM和RPCPSO-MKLSSVM 4种方法建立水泥熟料fCaO含量预测模型，其中LSSVM使用高斯径向基核函数，MKLSSVM均采用形如式（12）的等价核函数。

优化算法初始化参数如下：PSO算法中维数D =6，粒子总数为M =30，学习因子c1= c2= 2，惯性权重ω=0.9，最大迭代次数lmax= 85；RPCPSO算法中维数D =6、粒子总数M =30、学习因子RPCPSO-MKLSSVM的模型参数分别采用PSO算法和RPCPSO算法在式（19）的约束范围内寻优。表4为4种方法获得的模型参数。

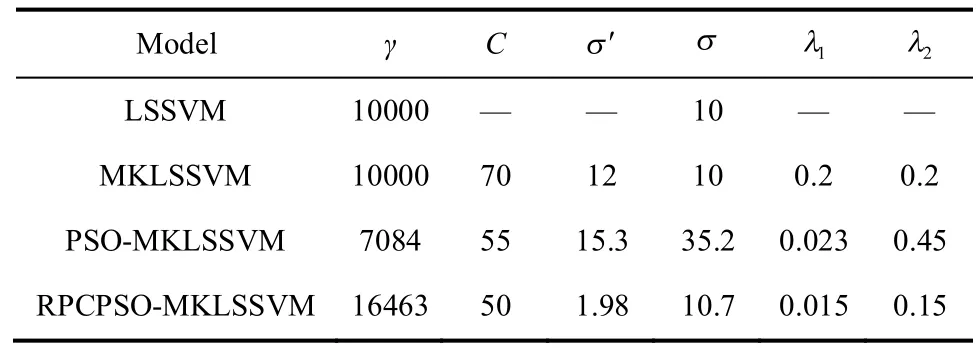
表4　4种方法建立的水泥熟料fCaO模型参数Table 4　Parameters of cement clinker fCaO models

由图1可以看出，采用RPCPSO算法训练过程中MSE达到1.37×10−4时，迭代次数为18次，并且当迭代次数达到随机扰动触发迭代次数后，算法跳出局部最优点，使均方误差降低为1.30×10−4，而采用标准PSO算法经过41次训练，均方误差只达到1.73×10−4并保持不变。仿真结果表明RPCPSO算法的收敛速度和精度均优于标准PSO算法。

图1　PSO和RPCPSO算法均方误差比较曲线Fig.1　MSE curve of PSO and RPCPSO algorithm

仿真实验所用的4种建模方法预测熟料fCaO含量仿真结果对比如图2所示。

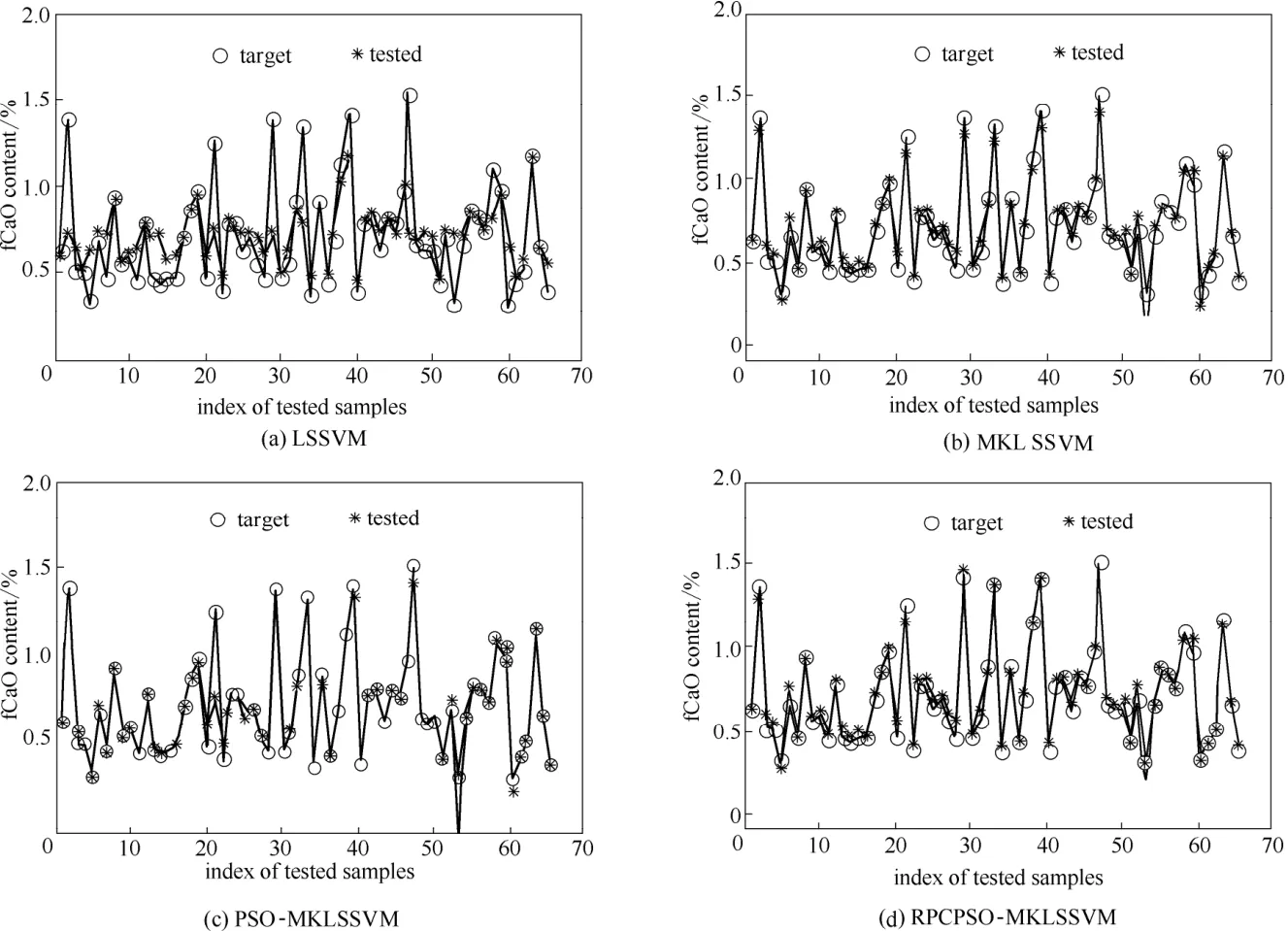
图2　4种方法预测水泥熟料fCaO含量仿真效果Fig.2　Simulation results of prediction cement clinker fCaO content by four methods

比较4种方法水泥熟料fCaO含量预测效果图可知，无参数优化的LSSVM和MKLSSVM方法建立的水泥熟料fCaO含量模型中真实值和预测值拟合程度相对有参数优化建立的模型较差，而且MKLSSVM方法建立的模型真实值和预测值拟合度强于单一核函数LSSVM方法建立的模型拟合度，表明本文给出的组合核函数MKLSSVM方法的建立的模型精度较高。另外比较PSO算法和RPCPSO算法优化的MKLSSVM仿真结果，RPCPSO算法优化MKLSSVM的仿真曲线拟合度比PSO算法优化MKLSSVM的曲线拟合度好，表明改进的RPCPSO算法具有更强的寻优能力。

为进一步比较本仿真实验所使用的4种方法建立的模型质量，采用可表示模型质量指标的最大绝对误差、平均绝对误差以及均方误差MSE作为评判指标。4种方法建立的水泥熟料fCaO含量预测模型性能指标如表5所示。

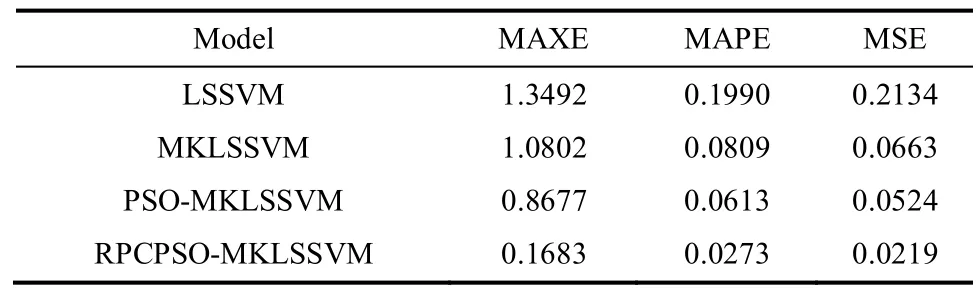
表5　4种模型性能统计Table 5　Performance comparison of four models

通过比较表5中数据可知，手动选取参数建立的LSSVM和MKLSSVM模型各项性能指标较差，模型精度较低，但MKLSSVM模型性能比LSSVM模型较好。通过比较寻优方法得到参数的两种建模方法可知，RPCPSO-MKLSSVM模型的各项性能指标均优于PSO-MKLSSVM模型，说明本文通过RPCPSO算法优化MKLSSVM模型参数建立的模型精度更高、泛化能力更强。

由表6[1]中fCaO含量与水泥安定性的关系可知，当fCaO含量超过一定值后，水泥安定性不合格，使用安定性不合格的水泥对建筑物寿命有较大影响。另外，由熟料fCaO的产生机理[3,8]可知，过低的fCaO值需要消耗大量的能源。因此，可采用本文提出的模型对熟料fCaO进行预测，使现场操作人员及工程师可根据fCaO值结合安定性和能耗对生产过程参数进行调整，以达到在保证安定性合格的基础上尽可能降低生产能耗的目的。由此可见，水泥熟料fCaO预测模型的研究对于水泥生产具有较大的指导意义。

表6　fCaO含量与水泥安定性的关系[1]Table 6　Relationship between cement soundness and fCaO content[1]

4　结　论

本文采用3种不同类型的核函数线性加权构建等价核，给出了一种MKLSSVM建模方法，并利用改进的RPCPSO算法针对MKLSSVM的6个待确定参数进行迭代寻优，提高了模型精度，避免了参数选取的盲目性。仿真分析结果表明，提出的RPCPSO算法搜索精度和收敛速度均优于对比算法，采用RPCPSO-MKLSSVM方法建立的水泥熟料fCaO预测模型的精度和泛化能力均高于其他3种对比方法。准确地预测熟料fCaO含量值不仅可以使操作人员和工程师根据fCaO值调整生产参数，为水泥生产提供指导，也为后续水泥生产过程优化操作以及智能控制提供了先决条件。

符号说明

b——MKLSSVM算法中常值偏差矩阵

C——多项式核函数参数

c——RPCPSO算法中学习因子

D——RPCPSO算法中待优化问题维度

ei——MKLSSVM算法的误差项

Lt——RPCPSO算法随机扰动触发条件

l——RPCPSO算法的进化代数

M——RPCPSO算法的粒子数量

pg，pi——分别为RPCPSO算法搜寻到的种群最优解和个体最优解

v——RPCPSO算法的粒子飞行速度

w——MKLSSVM算法中权值矩阵

z——一个混沌时间序列

αi，βi——MKLSSVM算法的拉格朗日乘子

γ——MKLSSVM算法中正则化系数

λ——MKLSSVM算法中核函数系数

σ——高斯径向基核函数核宽度参数

σ′——指数型核函数核宽度参数

ω——RPCPSO算法中惯性权重

下角标

i——输入、输出样本所属类别标记

References

[1]KAEWMANEE K, KRAMMART P, SUMRANWANICH T, et al. Effect of free lime content on properties of cement-fly ash mixtures [J]. Construction and Building Materials, 2013, 38: 829-836. DOI: 10.1016/j.conbuildmat.2012.09.035.

[2]王秀莲, 孙旭晨, 王卓, 等. 基于局部PSO-LSSVM的水泥f-CaO测量方法研究 [J]. 控制工程, 2014, 21 (6): 807-811. DOI: 10.3969/j.issn.1671-7848.2014.06.003. WANG X L, SUN X C, WANG Z, et al. Measurement method research for cement f-CaO based on local PSO-LSSVM [J]. Contorl Engineering of China, 2014, 21 (6): 807-811. DOI: 10.3969/j.issn.1671-7848.2014.06.003.

[3]LI W T, WANG D H, ZHOU X J, et al. An improved multi-source based soft sensor for measuring cement free lime content [J]. Information Sciences, 2015, 323: 94-105. DOI: 10.1016/j.ins.2015.06.035.

[4]李大字, 刘方, 靳其兵. 自增长混合神经网络及其在燃料电池建模中的应用 [J]. 化工学报, 2015, 66 (1): 333-337. DOI: 10.11949/j.issn.0438-1157.20141431. LI D Z, LIU F, JIN Q B. Self-growing hybrid neural network and its application for fuel cell modelling [J]. CIESC Journal, 2015, 66 (1): 333-337. DOI: 10.11949/j.issn.0438-1157.20141431.

[5]VAPNIK V N. An overview of statistical learning theory [J]. IEEE Trans. on Neural Networks, 1999, 10 (5): 988-999. DOI: 10.1109/72.788640.

[6]SUYKENS J A K, VANDEWALLE J. Least squares support vector machines classifiers [J]. Neural Network Letters, 1999, 19 (3): 293-300. DOI: 10.1023/A:1018628609742.

[7]SUYKENS J A K, VANDEWALLE J. Recurrent least squares support vector machines [J]. IEEE Trans. on Circuits and Systems, 2000, 47 (7): 1109-1114. DOI: 10.1109/81.855471.

[8]ZHENG P P, FENG J, LI Z, et al. A novel SVD and LS-SVM combination algorithm for blind watermarking [J]. Neurocomputing, 2014, 142: 520-528. DOI: 10.1016/j.neucom.2014.04.005.

[9]冯凯, 卢建刚, 陈金水. 基于最小二乘支持向量机的MIMO线性参数变化模型辨识及预测控制 [J]. 化工学报, 2015, 66 (1): 197-205. DOI: 10.11949/j.issn.0438-1157.20141636. FENG K, LU J G, CHEN J S. Identification and model predictive control of LPV models based on LS-SVM for MIMO system [J]. CIESC Journal, 2015, 66 (1): 197-205. DOI: 10.11949/j.issn.0438-1157.20141636.

[10]CHEN T T, LEE S J. A weighted LS-SVM based learning system for time series forecasting [J]. Information Sciences, 2015, 299: 99-116. DOI: 10.1016/j.ins.2014.12.031.

[11]刘瑞兰, 徐艳, 戎舟. 基于稀疏最小二乘支持向量机的软测量建模 [J]. 化工学报, 2015, 66 (4): 1402-1406. DOI: 10.11949/j.issn.0438-1157.20141392. LIU R L, XU Y, RONG Z. Modeling soft sensor based on sparse least square support vector machine [J]. CIESC Journal, 2015, 66 (4): 1402-1406. DOI: 10.11949/j.issn.0438-1157.20141392.

[12]AIOLLI F, DONINI M. EasyMKL: a scalable multiple kernel learning algorithm [J]. Neurocomputing, 2015, 169: 215-224. DOI: 10.1016/ j.neucom.2014.11.078.

[13]汪洪桥, 孙富春, 蔡艳宁, 等. 多核学习方法 [J]. 自动化学报, 2010, 36 (8): 1037-1050. DOI: 10.3724/SP.J.1004.2010.01037. WANG H Q, SUN F C, CAI Y N, et al. On multiple kernel learning methods [J]. Acta Automatica Sinica, 2010, 36 (8): 1037-1050. DOI: 10.3724/SP.J.1004.2010.01037.

[14]陈强, 任雪梅. 基于多核最小二乘支持向量机的永磁同步电机混沌建模及其实时在线预测 [J]. 物理学报, 2010, 59 (4): 2310-2318. DOI: 10.7498/aps.59.2310. CHEN Q, REN X M. Chaos modeling and real-time online prediction of permanent magnet synchronous motor based on multiple kernel least squares support vector machine [J]. Acta Physica Sinica, 2010, 59 (4): 2310-2318. DOI: 10.7498/aps.59.2310.

[15]FOSSACECA J M, MAZZUCHI T A, SARKANI S. MARK-ELM: application of a novel multiple kernel learning framework for improving the robustness of network intrusion detection [J]. Expert Systems with Applications, 2015, 42 (8): 4062-4080. DOI: 10.1016/ j.eswa.2014.12.040.

[16]安剑奇, 陈易斐, 吴敏. 基于改进支持向量机的高炉一氧化碳利用率预测方法 [J]. 化工学报, 2015, 66 (1): 206-214. DOI: 10.11949/j.issn.0438-1157.20141482. AN J Q, CHEN Y F, WU M. A prediction method for carbon monoxide utilization ratio of blast furnace based on improved support vector regression [J]. CIESC Journal, 2015, 66 (1): 206-214. DOI: 10.11949/j.issn.0438-1157.20141482.

[17]何巧乐, 崔国民, 许海珠. 基于新策略粒子群算法优化换热网络[J]. 化工学报, 2014, 65 (S1): 391-397. DOI: 10.3939/j.issn.0438-1157.2014.zl.063. HE Q L, CUI G M, XU H Z. Particle swarm optimization with two new strategies for heat exchangers network synthesis [J]. CIESC Journal, 2014, 65 (S1): 391-397. DOI: 10.3939/j.issn.0438-1157.2014.zl.063.

[18]NICKABADI A, EBADZADEH M M, SAFABAKHSH R. A novel particle swarm optimization algorithm with adaptive inertia weight [J]. Applied Soft Computing, 2011, 11 (4): 3658-3670. DOI: 10.1016/j.asoc.2011.01.037.

[19]田中大, 高宪文, 石彤. 用于混沌时间序列预测的组合核函数最小二乘支持向量机 [J]. 物理学报, 2014, 63 (16): 70-80. DOI: 10.7498/aps.64.030506. TIAN Z D, GAO X W, SHI T. Combination kernel function least squares support vector machine for chaotic time series prediction [J]. Acta Physica Sinica, 2014, 63 (16): 70-80. DOI: 10.7498/aps.64.030506.

[20]YAO X, LIU Y, LIN G M. Evolutionary programming made faster [J]. IEEE Trans. on Evolutionary Computation, 1999, 3 (2): 82-102. DOI: 10.1109/4235.771163.

[21]YANG C H, TSAI S W, CHUANG L Y, et al. An improved particle swarm optimization with double-bottom chaotic maps for numerical optimization [J]. Applied Mathematics and Computation, 2012, 219 (1): 260-279. DOI: 10.1016/j.amc.2012.06.015.

[22]SUN J, FANG W, PALADE V, et al. Quantum-behaved particle swarm optimization with Gaussian distributed local attractor point [J]. Applied Mathematics and Computation, 2011, 218 (7): 3763-3775. DOI: 10.1016/j.amc.2011.09.021.

Multiple kernel least square support vector machine model for prediction of cement clinker lime content

ZHAO Pengcheng1,2, LIU Bin1,2, GAO Wei3, ZHAO Zhibiao1,2, WANG Meiqi1,2
(1Institute of Information Science and Engineering, Yanshan University, Qinhuangdao 066004, Hebei, China;2Key Laboratory for Special Fiber and Fiber Sensor of Hebei Province, Qinhuangdao 066004, Hebei, China;3Institute of Electrical Engineering, Yanshan University, Qinhuangdao 066004, Hebei, China)

Abstract:Aiming at the problem of how to accurately predict the cement clinker fCaO content, the traditional single kernel least squares support vector machine (LSSVM) is difficult to show the complex non-linear relation between the clinker fCaO content and corresponding variables exactly. Thus, the multiple kernel least square support vector machine (MKLSSVM) containing three kernel function is presented based on multiple kernel learning to avoid the influence of the single kernel function on the model accuracy. As a result of artificial selection the parameters of MKLSSVM is blindness and uncertainty. The random perturbation chaos particle swarm optimization (RPCPSO) algorithm is presented to get the best parameters of MKLSSVM. The cement clinker fCaO content model is built by using the RPCPSO algorithm to optimize the parameters of MKLSSVM. Simulation results indicated that the RPCPSO algorithm had a fast convergence speed, and the model had high precision and strong ability of power generalization. Thus, the model was valuable for practical application.

Key words:multiple kernel learning; least square support vector machine; model; optimization; algorithm; random perturbation

中图分类号：TP 183

文献标志码：A

文章编号：0438—1157（2016）06—2480—08

DOI：10.11949/j.issn.0438-1157.20151598

基金项目：河北省自然科学基金项目（F2016203354）。

Corresponding author:Prof. LIU Bin, liubin@ysu.edu.cn