基于调制理论的24脉波整流机组直流侧谐波分析
陈 欢,宋平岗,罗 剑,戈 旺,朱维昌
(华东交通大学电气与电子工程学院,江西南昌330013)
基于调制理论的24脉波整流机组直流侧谐波分析
陈欢,宋平岗,罗剑,戈旺,朱维昌
(华东交通大学电气与电子工程学院,江西南昌330013)
摘要:目前国内大部分的城市轨道交通牵引变电所是采用24脉波整流机组对从降压变电所中所引入的交流电源进行整流。分析了24脉波整流机组的工作机理并对调制理论的基本原理作了简要阐述;从三相全桥6脉波整流电路出发,逐步推导出了不考虑换相角时的24脉波整流机组电压电流开关函数;在此基础上基于调制理论和时域FFT分析方法对理想状态下的24脉波整流机组的直流侧特征谐波进行了理论分析;最后在Matlab/Simulink中建立了仿真模型,验证了基于调制理论分析的直流侧特征谐波分布的正确性和有效性,从而为24脉波整流机组的交直流谐波分析提供了一种新的途径。
关键词:24脉波整流机组;开关函数;调制理论;FFT;特征谐波
1 引言
为减小三相整流器输入的总谐波含量,提高整体系统的电磁兼容性,采用将整流电路进行移相多重联结的方法得到了普遍采用。在一个电源周期中,整流装置输出的电压脉波数越多,则输出电压中的最小谐波阶次越高,其幅值也越小;同时流入整流装置的交流电流中的谐波频率越高,谐波电流幅值越小[1]。在城市轨道交通牵引供电系统领域,越来越多的牵引变电所是采用24脉波整流机组取代以前的6脉波或12脉波整流机组,以减少网侧输入电流的谐波含量,降低高次谐波对电网及其它设备的影响。当由24脉波整流机组构成的直流牵引供电系统处于理想稳态对称运行情况下时,整流机组的交流侧和直流侧均只产生特征谐波。
谐波分析的方法主要有时域法和频域法两种。文献[2]采用基于Newton-Raphson法对电压的基波和谐波潮流同时进行计算,但该策略存在以下缺点:(1)需要同时已知谐波源的电压和电流;(2)采用Newton-Raphson法分析计算时所列的方程组中Jacobi矩阵比较复杂,计算量繁重;(3)相类似的问题采用该分析方式时需要建立新的方程,可移植性差。文献[3]提出了一种谐波导纳矩阵法,其采用某一频域耦合导纳矩阵来模拟谐波所产生的相应特性。该方法考虑谐波之间的互相耦合,对谐波产生机理进行展现,相比其他频域方法,其具有模型准确、无需重复迭代等优点。但由于该频域耦合导纳矩阵中各元素取决于系统的运行参数和电路参数,在直流供电系统中运行的参数通常都是时变的,使得每次使用模型矩阵时需要重复进行计算,导致工作量也偏大。基于开关函数定义的适用于二极管不控整流电路和晶闸管相控整流电路的调制理论具有概念清晰、计算量小等优点,已经被广泛用于各种电力电子电路的建模和分析。基于此,本文采用调制理论和时域FFT分析方法对理想状态下的24脉波整流机组的直流侧谐波特性进行分析研究。
2 24脉波整流机组工作原理
如图1所示为24脉波整流机组的拓扑图。
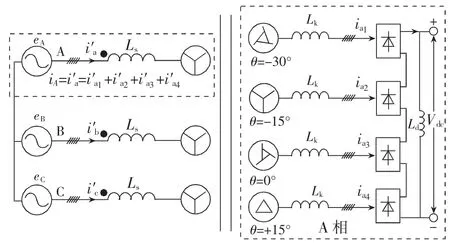
图1 24脉波整流机组拓扑图
城轨交通牵引变电所中的24脉波整流机组主要由2台相同容量的12脉波轴向双分裂式牵引移相整流变压器和4组由三相全波整流桥构成的整流器两部分共同组成。机组中的两台整流变压器阀侧均有两套低压绕组分别采用Y型接线和△型接线,使得两套绕组的线电天然形成30°的相位角。网侧绕组采用两种不同的延边三角形接线方式进行移相,左延△接法实现移相+7.5°,右延△接法实现移相-7.5°[4]。通过移相处理,得到的4套阀侧绕组的线电压就互差15°的相位角。它们各自经过由三相全波整流桥构成的整流器整流,在4组整流器的直流侧并联运行,组成2*12脉波整流系统,从而向牵引网输出24脉波的直流电源,为城轨列车提供牵引动力。
3 调制理论简介
以图(2)所示的典型的三相全桥六脉波整流电路为例,简要阐述调制理论的基本原理。
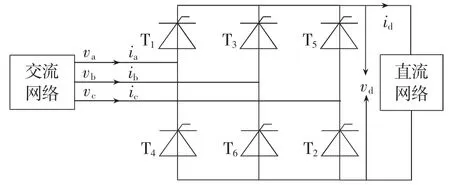
图2 三相全桥六脉波整流电路拓扑图
根据调制理论,整流电路中输出直流侧电压vd可以看作是输入的交流侧电压va、vb、vc被调制后的结果,输入的交流电源侧的三相相电流ia、ib、ic可以看作是输出直流侧电流id被调制后的结果,即vd以及相电流ia、ib、ic可表示为:

式中:Sva、Svb、Svc为交流侧三相电压va、vb、vc的开关函数,Sia、Sib、Sic为交流侧三相相电流ia、ib、ic的开关函数。
简单来讲,开关函数可以表示成变流器中电力电子器件的开或关的状态,但电路结构、电压和电流参考方向等因素会决定着其实际取值[5]。
对于图2中的三相全桥6脉波整流电路,交流侧A相电压的开关函数Sva定义如下:

同理可以得到B相电压和C相电压的开关函数Svb、Svc。
理想状态下,开关器件瞬时完成换相,不存在换相重叠角。对于A、B、C三相,其电压开关函数和电流开关函数完全相同[6]。应用调制理论对二极管不可控以及晶闸管相控整流电路进行谐波分析时,应按照交流侧相电压→直流侧电压、直流侧电流→交流侧相电流的次序依次进行[7]。
4 24脉波整流机组直流侧特征谐波分析
4.1 24脉波整流机组电压电流开关函数
在图2所示三相全桥6脉波整流电路中,利用时域FFT分析方法将其电压、电流的开关函数分解为Fourier级数的形式,如下所示:
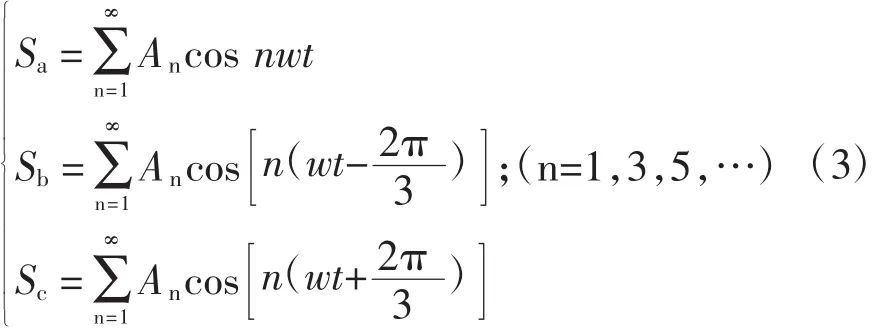
式中:An为各开关函数的系数;w为角频率。
本文将从三相全桥6脉波整流电路的电压电流开关函数出发,逐步推导出24脉波整流机组的电压电流开关函数。图3所示的(a)、(b)分别为不考虑换相角δ时和考虑换相角δ时的三相全桥6脉波整流电路a相电压开关函数Sva以及电流开关函数Sia的图形。
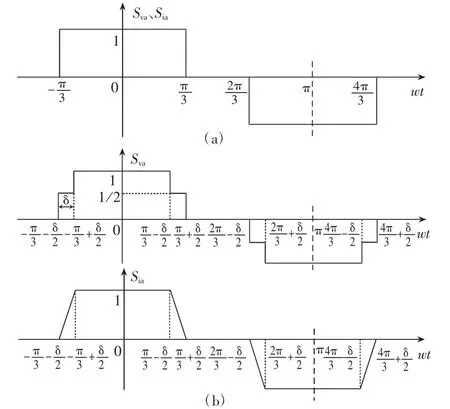
图3 三相全桥6脉波整流电路a相电压和电流开关函数
对于图3(a)中,由于不考虑换相角δ,根据基于开关函数定义调制理论的基本原理,可知电压开关函数Sva和电流开关函数Sia完全相等。根据图3所示的波形,两开关函数的系数An的计算式为:

对于图3(b)中,考虑换相角δ时,电压、电流开关函数Sva、Sia的系数Anu、Ani的计算式分别如下:

对于12脉波整流电路,它由2组6脉波整流电路并联或者串联所组成,其变压器的一、二次侧接线方式分别采用Y/Y形接线和Y/△形接线。由叠加原理,不考虑换相角δ时,12脉波整流电路开关函数为6脉波整流电路Y/Y接线和Y/△形接线各自的开关函数相叠加[8-10],其a相电压、电流的开关函数图形如图4所示。
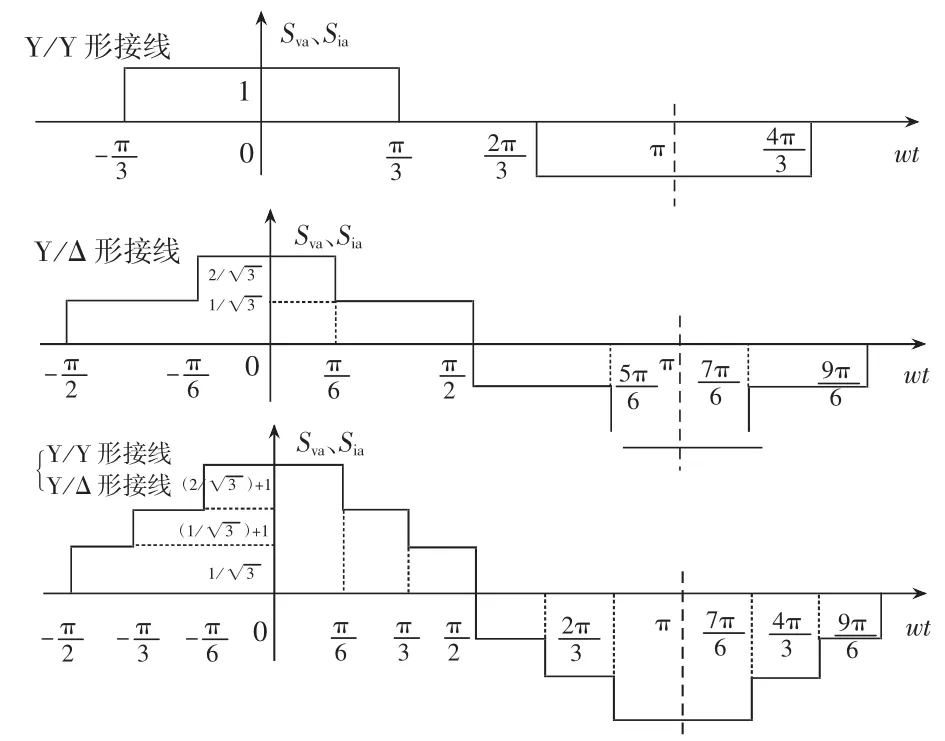
图4 12脉波整流电路a相电压和电流开关函数
根据图4所示开关函数波形,电压、电流开关函数的系数Bn的计算式为:
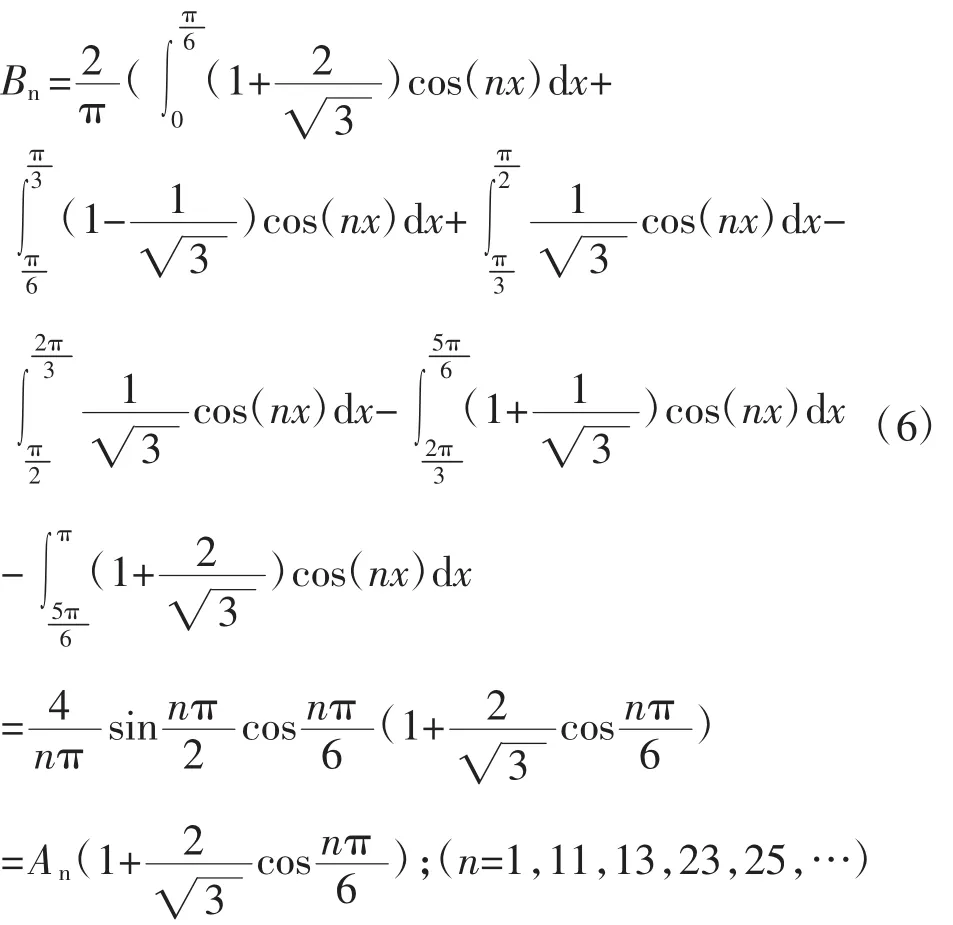
考虑换相角δ时,12脉波整流电路a相的电压、电流开关函数的系数Bnu、Bni分别为:
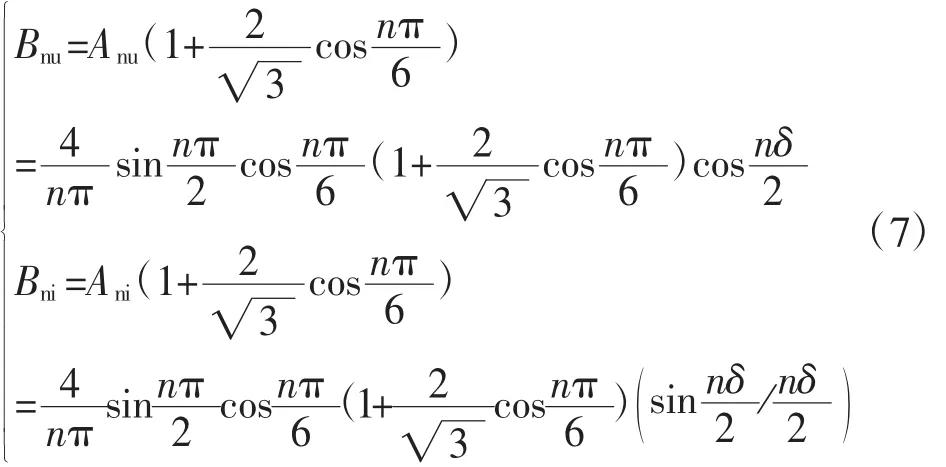
由叠加原理,不考虑换相角δ时,24脉波整流机组的a相电压、电流开关函数如图5所示。

图5 24脉波整流机组a相电压和电流开关函数
根据相类似的计算方法,不考虑换相角时24脉波整流机组电压、电流开关函数的系数Cn的计算式为:
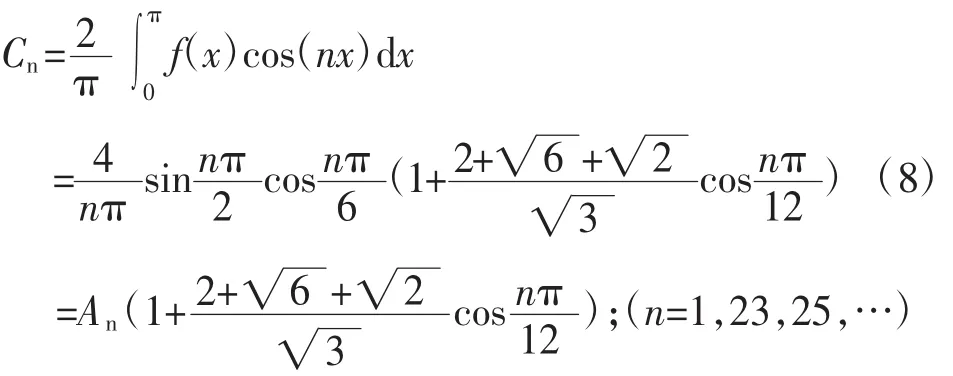
4.2直流侧谐波分析
设整流机组输入的三相电压为:

式中:Em为三相相电压的幅值;w为电网电压的角频率。
根据调制理论,输出直流电压Vdc可表示为:

公式(10)中S(vwt)为电压开关函数[Sv(awt),Svb(wt),Sv(cwt)]的向量表示形式。
根据式(3)可知,此时不考虑换相角δ时24脉波整流机组的电压电流开关函数为:
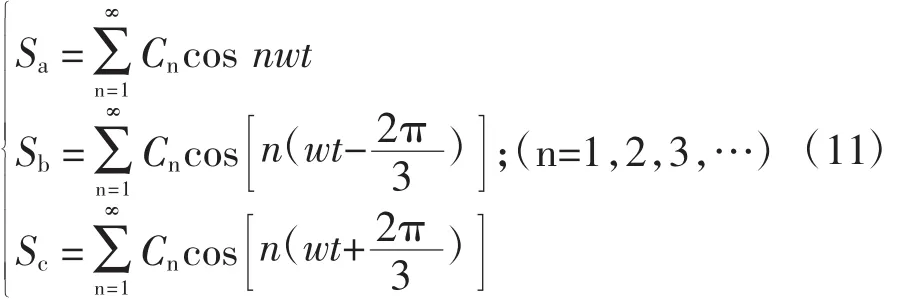
根据调制理论,整流机组输出的直流电压Vdc是输入侧的三相电压Es经过电压开关函数Sv调制后所得,此时:

假定24脉波整流机组所带负载为阻感性负载,由电路理论,可得24脉波整流机组输出侧的直流电流Idc为:
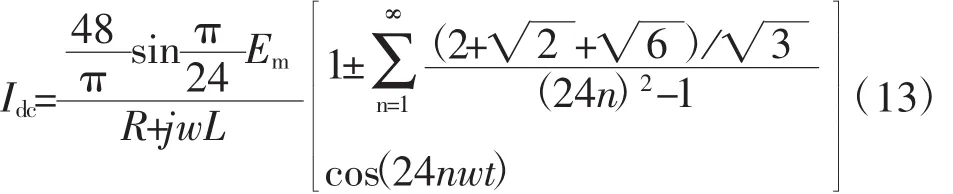
由公式(13)可知,在理想状态下,城轨24脉波整流机组的直流侧的输出电流仅含有24n (n=1,2,3,…)次谐波分量,各谐波分量的幅值也随着频率的不断增大而以1/(24n)2的速度逐渐衰减。
5 仿真验证
本文基于Matlab/Simulink平台构建24脉波整流机组模型进行仿真。仿真模型主要参数设定如下:三相电压源Uabc为工频50Hz,线电压有效值为35kV;单台整流变压器的额定容量S为1000kVA;整流变压器一、二次侧的电压变比为:33000:180:1180;负载电阻R为20Ω,负载电感L 为1e-8H,仿真时间为0.06s,仿真波形及其频谱图如图6所示。
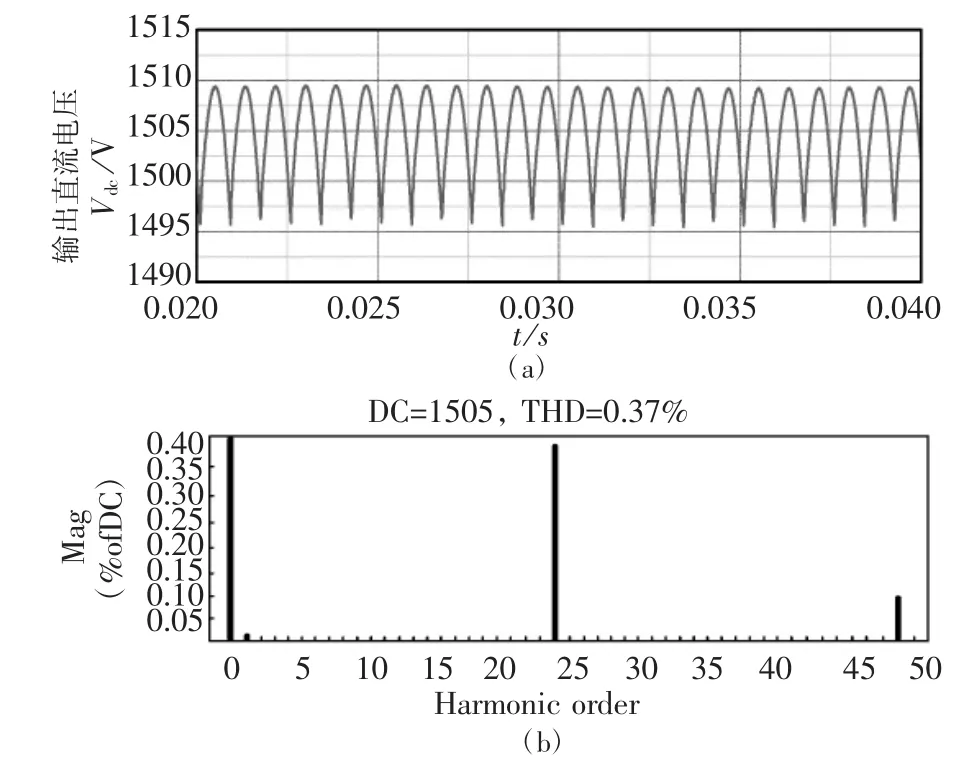

图6直流侧电压电流波形图及其频谱图
图6中,图(a)、(c)分别为24脉波整流机组输出直流电压和电流的波形图。电压电流波形在一个交流周期0.02s之内脉动24次,每个脉动的角度间隔为15°,脉动较为平稳,输出的直流电压存在一定的电压纹波。图(b)和图(d)为输出直流电压和电流的谐波频谱图,由频谱图可知:在不考虑换相角时,24脉波整流机组的直流侧电压、电流谐波只含有24n(n=1,2,3,…)次谐波分量,且谐波分量的幅值随着谐波频率的不断增大而逐渐衰减,从而验证了不考虑换相角时基于调制理论所分析24脉波整流机组直流侧特征谐波分布的正确性和有效性。
6 结束语
以三相全桥6脉波整流电路开关函数为基础,逐步推导出不考虑换相角时的24脉波整流机组电压、电流的开关函数。根据调制理论的基本原理,将24脉波整流机组输出直流侧电压和电流分别用整流机组输入侧正弦电压和电压开关函数来表示,从而对不考虑换相角时的24脉波整流机组直流侧的特征谐波分布进行分析,并得出其分布规律:在理想状态下,24脉波整流机组的直流侧谐波只含有24n(n=1,2,3,…)次谐波分量,且谐波分量的幅值也随着频率的不断增大而逐渐衰减。在Matlab/Simulink平台建立仿真模型,仿真结果验证了基于调制理论的直流侧谐波分析的正确性和有效性,这为二极管不可控及晶闸管相控整流电路的交直流侧谐波分析提供了一种新途径。
参考文献:
[1]秦萌涛,宋文武,黄琛.舰用12脉波整流器直流侧谐波分析[J].舰船科学技术,2015,37(2).
[2]张大海,毕艳冰,毕研秋,等.电力逆变器调制理论的扩展研究[J].电网技术,2010,34(12):63-67.
[3]李琼林,刘会金,张振环,等.基于互调制原理的交直交变流系统中的谐波分析[J].中国电机工程学报,2007,27 (34):107-114.
[4]全恒立,刘志刚,张钢,等.地铁24脉波整流器空载直流侧谐波特性分析[J].铁道学报,2012,34(3):28-33.
[5]杨小兵,李兴源,金小明,等.基于调制理论的换流变压器铁芯饱和及不稳定分析[J].电网技术,2009,33(20):49-53.
[6]梁继云,康积涛.调制理论在交直流输电系统谐波分析中的运用[J].华电技术,2011,33(11):52-53.
[7]肖超,刘跃,张仁红.HVDC中调制理论谐波研究[J].现代机械,2013,12(4):86-89.
[8]Wang Y,Joos G,Jin H.DC-side shunt-active power filter for phase-controlled magnet-load power supplies[J].IEEE Trans on Power Electronics,1997,12(5):765-771.
[9]余瑜,刘开培,陈俊,等.基于调制理论的高压直流输电系统混合谐振型谐波不稳定判据[J].高电压技术,2014,40(5):1582-1589.
[10]杜登明,罗隆福,雷园园,等.基于开关函数法的新型换流变压器谐波分析[J].电气传动,2010,40(2):52-56.
Harmonic analysis of 24-pulse rectifier unit at the DC side based on modulation theory
CHEN Huan,SONG Ping-gang,LUO Jian,GE Wang,ZHU Wei-chang
(College of Electrical and Electronic Engineering,East China Jiaotong University,Nanchang 330013,China)
Abstract:At present,most of the domestic urban rail transit traction substations adopt the 24-pulse rectifier unit to rectify the AC power from the step-down transformer substations.The working mechanism of 24 pulse rectifier and the basic principle of the modulation theory are presented.Started from the three-phase full-bridge 6-pulse rectifier circuit,the voltage and current switching functions of the 24-pulse rectifier unit without considering the commutation angle are derived gradually.Based on the modulation theory and time-domain FFT analysis method,the harmonic characteristics of 24-pulse rectifier unit at the DC side under the ideal state are analyzed in theory;The simulation model is established with Matlab/Simulink software to verify the correctness and the validity of the harmonics distribution at the DC side under the ideal state based on the modulation theory,which provides a new way for the harmonic analysis of 24-pulse rectifier unit both at the AC side and the DC side.
Key words:24-pulse rectifier unit;characteristic harmonic;switching function;modulation theory;FFT
中图分类号:TM922
文献标识码:A
文章编号:1005—7277(2016)02—0028—06
作者简介:
陈欢(1991-),男,硕士研究生,研究方向为电力电子与电力传动。
宋平岗(1965-),男,教授,博士,博士生导师,研究方向为电力电子与再生能源系统以及电力电子与电力传动。
收稿日期:2015-10-30

