基于方差分析对《概率论与数理统计》的教学思考

赵彩霞 席冬冬 陈英 王太荣

【摘要】引入统计软件，培养学生的应用能力是《概率论与数理统计》课程改革的必然趋势.本文选取同一专业的2个班级进行对比试验，利用单因素方差分析对两种教学方法进行了深入对比研究.

【關键词】方差分析；概率论；数理统计

一、引 言

《概率论与数理统计》是一门研究随机现象及其规律的数学基础学科，有着很强的理论性和应用性.目前很多高校在此门课程上只重视数学理论知识的学习，忽视学生应用能力的培养.为此，现抽取同一专业2个班级进行对比试验，假设两个班级学生的基础相当，同一授课教师在两个班级中分别使用不同的教学方法：1班使用传统教学方法，2班使用引入统计软件的教学方法.其他条件例如教学内容、考试内容等基本一致，学期后通过期末概率论与数理统计成绩进行比较分析，主要分析方法为单因素方差分析.

二、单因素方差分析基本原理

方差分析可分为单因素方差分析、多因素方差分析，以及协方差分析.

（一）单因素方差分析的基本思想

单因素方差分析用来研究一个控制变量的不同水平是否对观测变量产生了影响.这里将“概率论与数理统计成绩”作为观测变量，“教学手段” 作为控制变量.单因素方差分析的思想重在剖析观测变量的方差，认为观测变量值的变动受到控制变量和随机变量两方面的影响.将观测变量总的离差平方和（SST）分解成组间离差平方和SSA和组内离差平方和SSE，其数学表述为：SST=SSA+SSE.通过比较观测变量总离差平方和中各部分所占的比例，推断控制变量是否对观测变量带来了显著影响.

（二）单因素方差分析的数学模型

三、实证分析

现利用SPSS 17.0软件分析不同教学方法对学生概率论与数理统计期末成绩的影响.选择菜单“分析→均值比较→单因素ANOVA”，将“概率论与数理统计成绩”作为观测变量，“教学手段” 作为控制变量进行单因素方差分析.

（一）方差齐性检验结果

不同教学方法下期末成绩的方差齐性检验值为2.243，其相伴概率为Sig.=0.137，如果显著性水平设为0.05，由于相伴概率大于显著性水平，认为不同教学方法下期末成绩的总体方差是相等的，满足了方差分析的前提条件.

（二）不同教学方法的方差检验结果

观测变量期末成绩的总离差平方和为11847.873，可解释的变差为2897.507，自由度为1，均方为2897.507；抽样误差引起的变差为8950.366，自由度为124，均方为72.180；相除所得的F 统计量的观测值为40.143.1其相伴概率Sig.=0.000<显著性水平0.05，认为不同教学方法对概率论与数理统计期末成绩产生了显著影响.

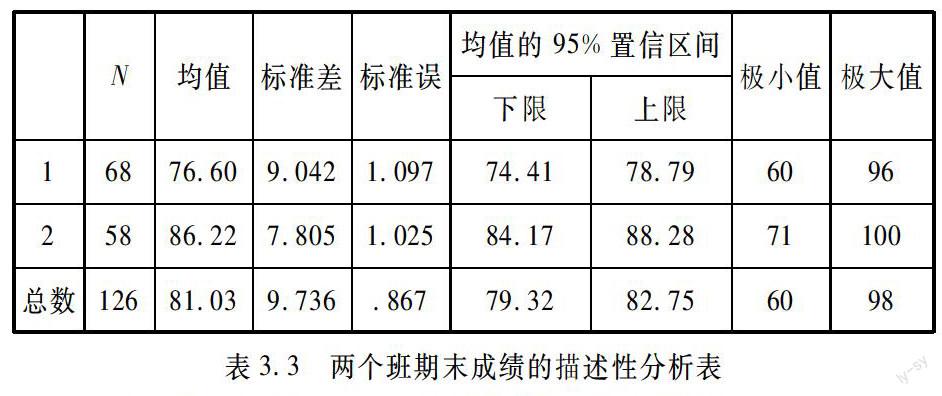
（三）表3.3表明，2班的平均成绩明显高于1班，即引入统计软件的教学方法优于传统教学方法

四、对《概率论与数理统计》课程的教学思考

通过两个班级的期末成绩进行实证分析，得知引入统计软件的教学方法优于传统教学方法.建议在以后的课堂上可以将理论知识与实际背景相结合，引入SPSS等统计软件，更好的培养学生分析和解决实际问题的能力.加强SPSS等软件的介绍，使学生了解和熟悉运用软件进行数据分析，提高学生的学习兴趣，培养学生的动手能力.

【参考文献】

薛薇.SPSS统计分析方法及应用[M].北京：电子工业出版社，2013.