基于博弈模型的PPP项目共担风险损失分配的研究

刘涛　　赖应良

[摘要]风险分担是PPP项目融资模式需要解决的核心问题之一，不合理的风险分担不仅增加投资成本，甚至将造成项目融资的失败。文章基于博弈理论，构建了公共部门与私人部门在风险损失分配谈判中所需的轮流出价的讨价还价博弈模型。以期得到较为合理的PPP项目中共担风险损失分配的方案，并提出有利于公私双方的合理化建议。

[关键词]PPP；博弈模型；共担风险

[DOI]1013939/jcnkizgsc201625165

PPP（Public-Private-Partnership）是指公共部门和私人部门通过建立合作伙伴关系来提供公共产品或服务的一种融资和项目管理模式。该模式可以解决公共基础设施建设中资金需求量大、融资困难、风险多且难以控制等问题，可以发挥私营部门技术雄厚、管理经验丰富的优势，有效改善资源配置，提高企业的生产效率，实现公共部门和私人部门的利益共享机制，为双方的“双赢”提供良好的合作基础[1]。PPP项目融资模式兼具基础设施和公用事业的特殊性质。投资规模大、建设和运营周期长、项目参与方众多、风险因素多等特征，使得 PPP 模式较传统的融资模式面临着更大的风险，如何合理分担风险是此类项目取得成功的关键因素。

本文在此背景下，在分析和归纳总结相关文献中共担风险的承担原则的基础上，构建了一套基于博弈模型的PPP项目共担风险损失分配体系，以期得到较为合理的PPP项目中共担风险损失分配的方案，并提出有利于公私双方的合理化建议。

1博弈论的基本概念

博弈论是关于策略决策制定的科学，是对两个或多个理性、智能的参与人之间相互影响的冲突与合作行为的研究。其核心问题在于，各方参与人如何在“策略互动”的局势中做出最佳决策，获得最大收益。博弈论的基本概念包括参与人、信息、战略、支付（或效用）和均衡。

参与人：是指在博弈中独立决策、独立承担后果的个人或组织。一个博弈模型中至少会有两个参与人。

信息：是博弈参与人掌握的各方互相影响博弈策略选择的实际信息。信息使某些情况得以排除，同时，在给定的信息范围内又有一些情况不能区分。

战略：是博弈参与方在给定信息集的情况下的博弈行为。在参与人同时一次行动博弈问题中，战略与行动是直接对应的。在有先有后的多次行动的博弈问题中，参与人将依据已经观察到其他参与人如何行动的信息来制定战略。

支付（或效用）：是在一个特定的策略组合下参与人得到的期望支付水平或效用水平。是参与人对战略实施时所产生结果的评价。

均衡：是指按特定的规则求得的博弈模型的最优解。

2共担风险损失分配的博弈分析

在风险损失分配谈判中最常见的谈判方式是轮流出价的讨价还价博弈模型。纳什对讨价还价问题做了深入地分析和探讨，并得出了纳什讨价还价解是一个合作博弈模型解，它是由帕累托有效性、效用测度的无关性、无关选择的独立性和对称性等公理推导出来的结果。在实际的讨价还价中，这些公理都是在背后起作用，但讨价还价通常是一个不断的“接受—不接受”过程。由于谈判成本的存在，讨价还价不会无限进行下去，谈判过程中的一方可能因无法承受谈判成本而接受报价。

假设公共部门和私人部门共同分担一块大小为π（π>0）的风险损失，双方出价在不连续的时点上进行。在奇数时点上，公共部门提出自己不需要承担的风险损失份额为X，则私人部门不需要承担的风险损失份额为1-X，私人部门可以接受，否则在偶数时点上提出新的公共部门风险损失分担份额。如此反复进行，当且仅当其中的一个参与人接受了出价则谈判结束[2]。

3博弈模型的建立和求解

在建立公私双方轮流出价的讨价还价博弈模型之前，需要结合项目的实际情况，提出如下合理的假设条件：

假设一：谈判中只有两个参与人，分别是公共部门G和私人部门S，且它们都希望谈判最终达成一致协议；

假设二：参与人G和S处于相互平等的地位，但公共部门G作为招标方先行出价；

假设三：分别用δ1和δ2表示公共部门G和私人部门S的谈判损耗系数，δ1∈（0，1]，δ2∈（0，1]。

假设四：博弈双方均知道谈判损耗系数的大小。

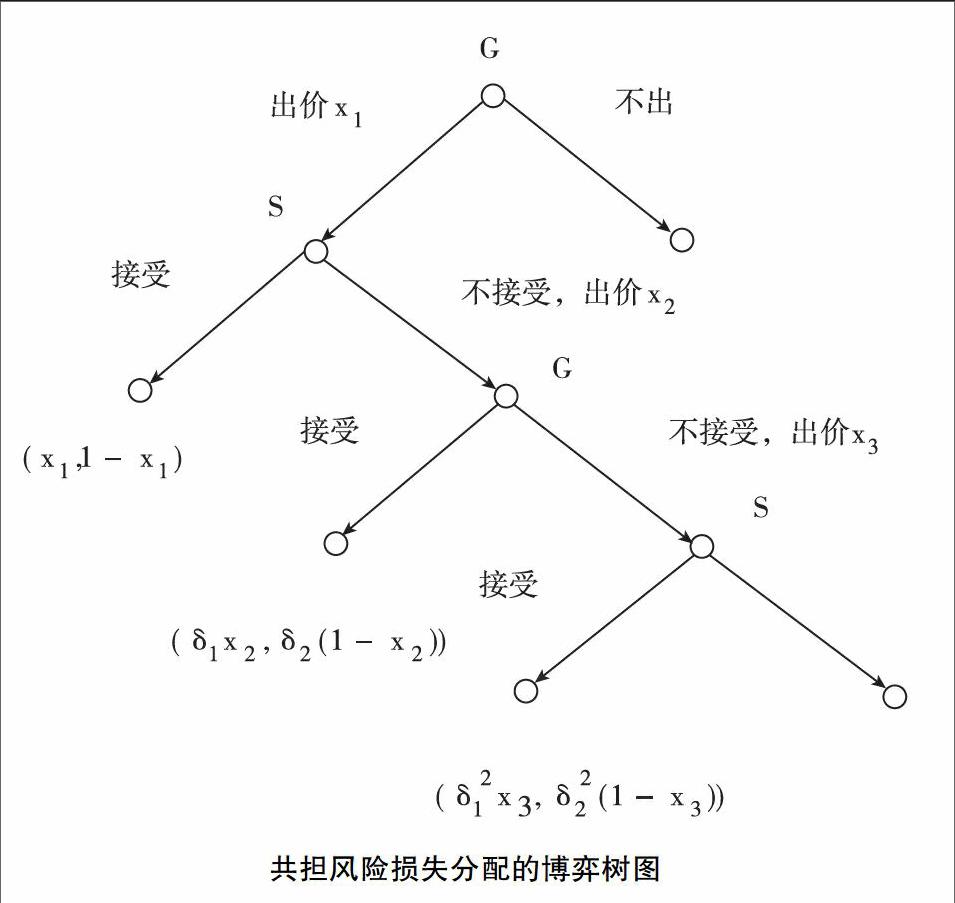
共担风险损失分配的博弈树下图所示。

共担风险损失分配的博弈树图

罗宾斯经过研究得出，无限期轮流出价模型存在唯一的子博弈精炼纳什均衡[3]，可以通过逆推得出此均衡解。本文选择有限期中的三阶段讨价还价作为无限期讨价还价逆推的起始节点。

第一回合：公共部门提出自己不需要承担的风险损失份额为X1，则私人部门不需要承担的风险损失份额为1-X1即：

公共部门：G1=X1（1）

私人部门：S1=1-X1（2）

其中，G1表示公共部门在第一回合不需要承担的风险损失比例，S1表示私人部门在第一回合不需要承担的风险损失比例。如果私人部门拒绝，则博弈进入第二回合。

第二回合：私人部门提出公共部门不需要承担的风险损失份额为X2，则自己不需要承担的风险损失份额为1-X2。但因为进入第二回合谈判会增加双方的谈判成本，因此公私双方不需要承担的风险损失比例要开始考虑谈判损耗系数：

公共部门：G2=δ1X2（3）

私人部门：S2=δ2（1-X2）（4）

如果公共部门拒绝，则谈判进入第三回合。

第三回合：公共部门提出自己不需要承担的风险损失份额为X3，则私人部门不需要承担的风险损失份额为1-X3，同时考虑谈判损失系数，得到公私双方在第三回合不需要承担的风险损失比例：

公共部门：G3=δ21X3（5）

私人部门：S3=δ22（1-X3）（6）

再往回看第二回合，如果私人部门提出的方案使得公共部门不需要承担的风险损失比例G2小于第三回合中公共部门不需要承担的风险损失比例G3，则公共部门肯定不会同意该回合的谈判结果，谈判不得不拖入第三回合。所以为了避免谈判进入到第三回合以产生不必要的损耗，且使得自己不需要承担的风险也最大化，私人部门最优战略是：

G2=G3（7）

即，δ1X2=δ21X3（8）

X2=δ1X3（9）

此时，私人部门不需要承担的风险损失比例S2为：

S2=δ2（1-δ1X3）（10）

又可知S3=δ22（1-X3），故把S2与S3比较可知S2>S3，即在第二回合的谈判中，公共部门和私人部门都不会把谈判拖入第三回合中。

再看第一回合，为了避免谈判进入到第二回合以产生不必要的损耗，且使得自己不需要承担的风险也最大化，公共部门最优战略是：

S1=S2（11）

将式（2）和式（10）代入式（11）得：

1-X1=δ2（1-δ1X3）（12）

即有：

X1=1-δ2（1-δ1X3）=1-δ2+δ1δ2X3（13）

又因为从第一回合开始的无限讨价还价博弈等于三回合博弈[4]，因此，公共部门在第三回合的出价具有强制性，即为最终的出价。即有：

X3=X1=1-δ2+δ1δ2X3（14）

得到，X*=（1-δ2）/（1-δ1δ2）（15）

则1-X*=δ1（1-δ2）/（1-δ1δ2）（16）

即为公私双方讨价还价模型的子博弈精炼纳什均衡解。

4结论

由式（15）可以看到，公共部门和私人部门需要承担的风险比例取决于（1-δ2）/（1-δ1δ2）的大小，（1-δ2）/（1-δ1δ2）越大，公共部门承担的风险损失比例越小，私人部门则越大。

公共部门应采取的战略是：在自己出价时，总是要求（1-δ2）/（1-δ1δ2）的不承担风险损失比例；在私人部门出价时，只接受任何大于或等于（1-δ2）/（1-δ1δ2）的不承担风险损失比例。同理，私人部门应采取的战略是，在公共部门出价时，只接受任何小于或等于δ1（1-δ2）/（1-δ1δ2）的不承担风险损失比例；在自己出价时，总是要求δ1（1-δ2）/（1-δ1δ2）的不承担风险损失比例。

参考文献：

[1]元霞，柯永建，王守清基于案例的中国PPP项目的主要风险因素分析[J].中国软科学，2009（5）：107-113

[2]阿伯西内，穆素讨价还价理论及其应用[M].上海：上海财经大学出版社，2005

[3]Rubinstein APerfect Equilibrium in a Bargaining Model[J].Econometrica，1982（50）：97-109

[4]谢识予经济博弈论[M].2版上海：复旦大学出版社，2002，146-165