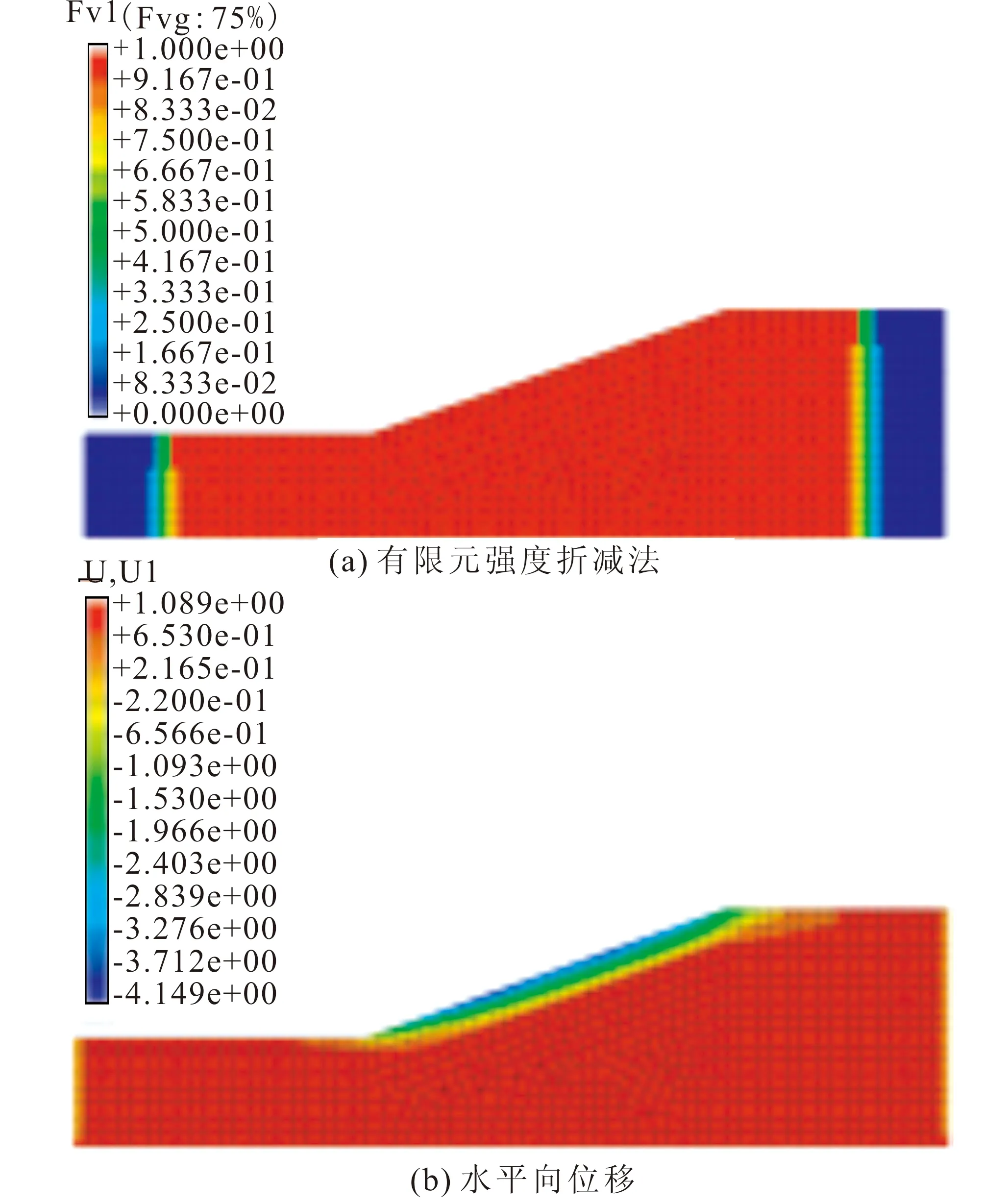
黏性土坡地震失稳机制及其在黄土斜坡地震稳定性分析中的应用①

赵文琛， 吴志坚,2， 陈豫津

(1.中国地震局兰州地震研究所 黄土地震工程重点实验室，甘肃 兰州 730000；2.甘肃省岩土防灾工程技术研究中心，甘肃 兰州 730000)

黏性土坡地震失稳机制及其在黄土斜坡地震稳定性分析中的应用①

赵文琛1， 吴志坚1,2， 陈豫津1

(1.中国地震局兰州地震研究所 黄土地震工程重点实验室，甘肃 兰州 730000；2.甘肃省岩土防灾工程技术研究中心，甘肃 兰州 730000)

摘要：基于地震作用下黏性土坡失稳滑动特点，以土体应力状态及其变化分析边坡失稳过程。通过分析地震作用下边坡不同部位土体应力状态和剪应力变化，结合实际地震边坡失稳破坏特征，提出黏性土坡地震三段式滑动失稳机制。在分析该滑动失稳机制与有限元强度折减法之间应力关联的基础上，将两者结合应用于实际黄土地震滑坡动力稳定性分析。依据此考虑得到的动力安全系数相比较其他方法，与极限平衡法得到的结果更为接近。

关键词：黏性土坡滑动失稳机制； 边坡地震稳定性分析； 有限元强度折减法

0引言

地震边坡失稳机理和边坡地震稳定性分析是构成边坡地震稳定性研究的两大主要内容。随着室内外土体测试技术与土工数值分析方法的进步，两者都得到了长足的发展并形成了各自的理论体系[1-8]。然而，目前对于边坡地震失稳机理与稳定性分析的研究少有交叉和融合，将二者综合考虑用于边坡稳定性研究的理论和方法为数更少。

地震边坡失稳机理往往偏重于以地震惯性力和孔隙水压力为根本诱因进行定性分析[1-4]，对坡体应力分布及变化特征关注较少，导致大多数的地震边坡失稳机理很难与目前边坡地震稳定性分析法中较为成熟的有限元方法相结合。

以极限平衡法和有限元法为代表的边坡地震稳定性分析方法大都专注于给出边坡动力安全系数和动力响应特征，而忽视对地震边坡失稳机理的研究[5-8]。因此，探寻合适的地震边坡失稳机理，发掘其与边坡地震稳定性分析方法间的内在联系，提出考虑地震边坡失稳机理的边坡地震稳定性分析方法，具有重要的理论意义和应用价值。

1反映边坡土体应力变化特征的地震边坡失稳机制

边坡土体应力是地震边坡失稳机理与边坡地震稳定性分析方法的重要联系，要将两者结合应用于分析边坡地震稳定性，则需分析边坡失稳过程中土体应力变化特征。

1.1地震作用下黏性土坡的受力特点及滑动模式

由于黏聚力的存在，黏性土坡不会像无黏性土坡一样沿坡面滑动[9]，在地震作用下其滑动面多表现为上陡下缓，破坏和滑动通常呈现出滑裂面高于坡脚、滑裂面穿过坡脚和滑裂面低于坡脚三种类型(图1)。

图1　地震作用下黏性土坡滑动示意图Fig.1　Sliding diagram of cohesive soil slope under earthquake

与静力作用下不同，处在地震作用下的土体，其应力状态是由地震形成的动应力和自重形成的静应力的叠加，且动应力的大小和方向时刻都在变化。地震作用下的垂直动应力σn和水平动应力σs定义为[10]：

(1)

(2)

(3)

(4)

式中:ρ为土体密度；vn、vs分别为土体中质点的竖向及水平向振动速度；cn为纵波波速；cs为剪切波速；K为体积变形模量；G为剪切模量。

取动应力最大值和最不利于稳定的方向，则边坡一点土体应力状态如图2所示[10]。一般认为地震以横向作用为主，故取σs>σn[8]。

图2　地震作用下土体应力状态Fig.2　Stress state of soil under earthquake

任意的黏性土坡都能简化为图3所示的平面斜坡形式。借鉴王恭先[11]提出的滑坡三段式滑动模式，以斜坡不同位置土体应力状态及变化来描述斜坡失稳状态，将地震作用以上述动应力的形式引入，按几何形态特征将黏性土边坡划分为坡底、坡面、坡顶三段，分别分析地震作用下黏性土坡受力特点。

图3　黏性土坡分段受力示意图Fig.3　Distribution of the stress in different segments of cohesive soil

如图3所示，对于三种类型的黏性土滑坡在失稳过程中受滑裂面形成及滑动的影响，坡顶段土体的竖直向大主应力基本保持不变，水平向小主应力减小。在坡顶段土体的挤压和坡底段土体的阻碍作用下，坡面段土体大致与坡面平行的大主应力和与其垂直的小主应力均增大。对于前两种类型的滑坡，滑裂面在坡面出露，坡底段土体只会受到微弱的挤压作用。而对于第三种类型的滑坡，滑裂面在坡底段表面出露，坡底段土体由于受到坡面段土体和坡顶段土体的推力，致使其分别平行和垂直于滑动面的大主应力和小主应力均增大。受地震横竖向拉张作用(σs和σn)影响，坡顶段土体大主应力和小主应力均被削弱，坡面段土体大主应力被削弱，小主应力转变为拉应力后得到加强，坡底段土体大主应力和小主应力也都遭到削弱。

1.2地震作用下黏性土坡失稳土体应力变化特征

为半定量化分析地震作用下黏性土坡失稳滑动过程中不同受力段土体的应力状态变化，以图3所示的一般平面土坡为分析对象，分别选取位于坡底段、坡面段及坡顶段内且埋深均为h，铅垂向应力σz相等的B、M、T三点处的土体(图4)，分析计算不同受力段土体在地震作用下边坡失稳前后的应力状态，揭示其剪应力变化规律。

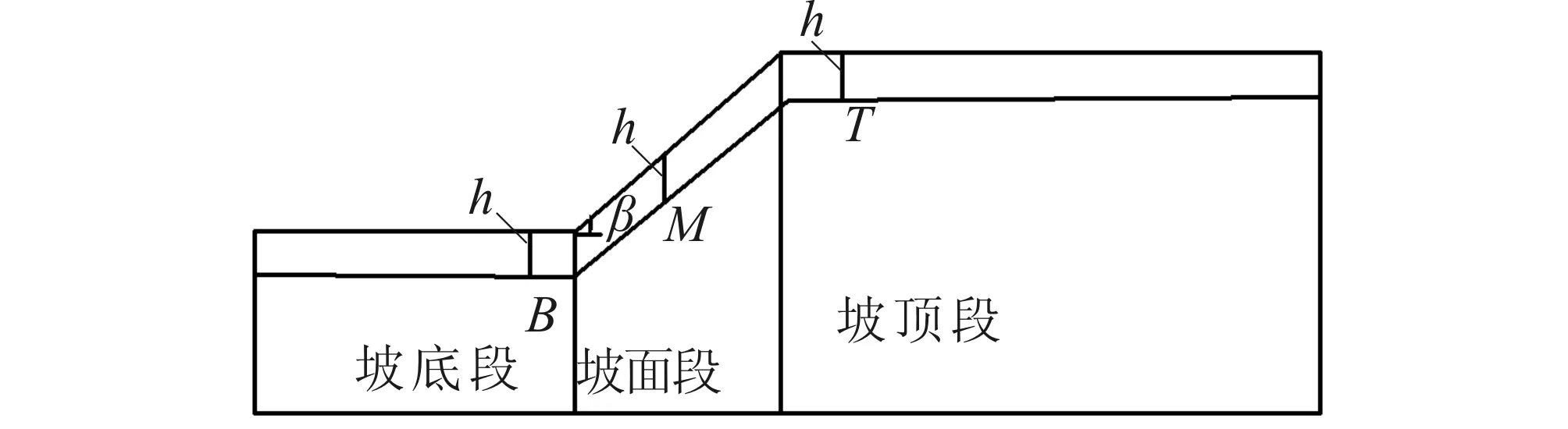
图4　平面黏性土坡土体受力分析示意图Fig.4　Schematic diagram of soil stress in plane cohesive soil slope

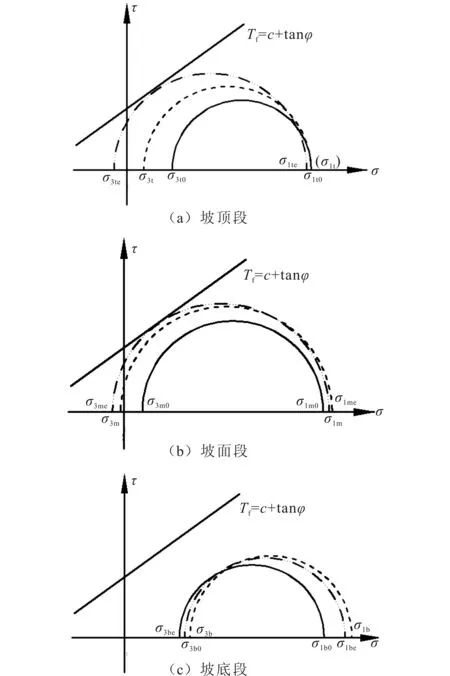
图5为边坡稳定时(σ0)和地震作用下开始失稳时(σe)不同受力段的应力状态。受滑裂面形成及滑动的影响，坡顶段T点土体小主应力σ3t逐渐减小；受坡顶段的挤压和坡底段的阻碍作用，坡面段M点土体大主应力σ1m增大，小主应力σ3m则由压应力逐渐减小并转变为拉应力；在坡面段蠕动土体的挤压下，坡底段B点土体大主应力σ1b和小主应力σ3b都逐渐增大。受地震横竖向拉张作用(σs和σn)影响，坡顶段T点土体大主应力σ1t和小主应力σ3t均被削弱，坡面段M点土体大主应力σ1m被削弱，小主应力σ3m转变为拉应力后得到加强，坡底段B点土体大主应力σ1b和小主应力σ3b也都遭到削弱。

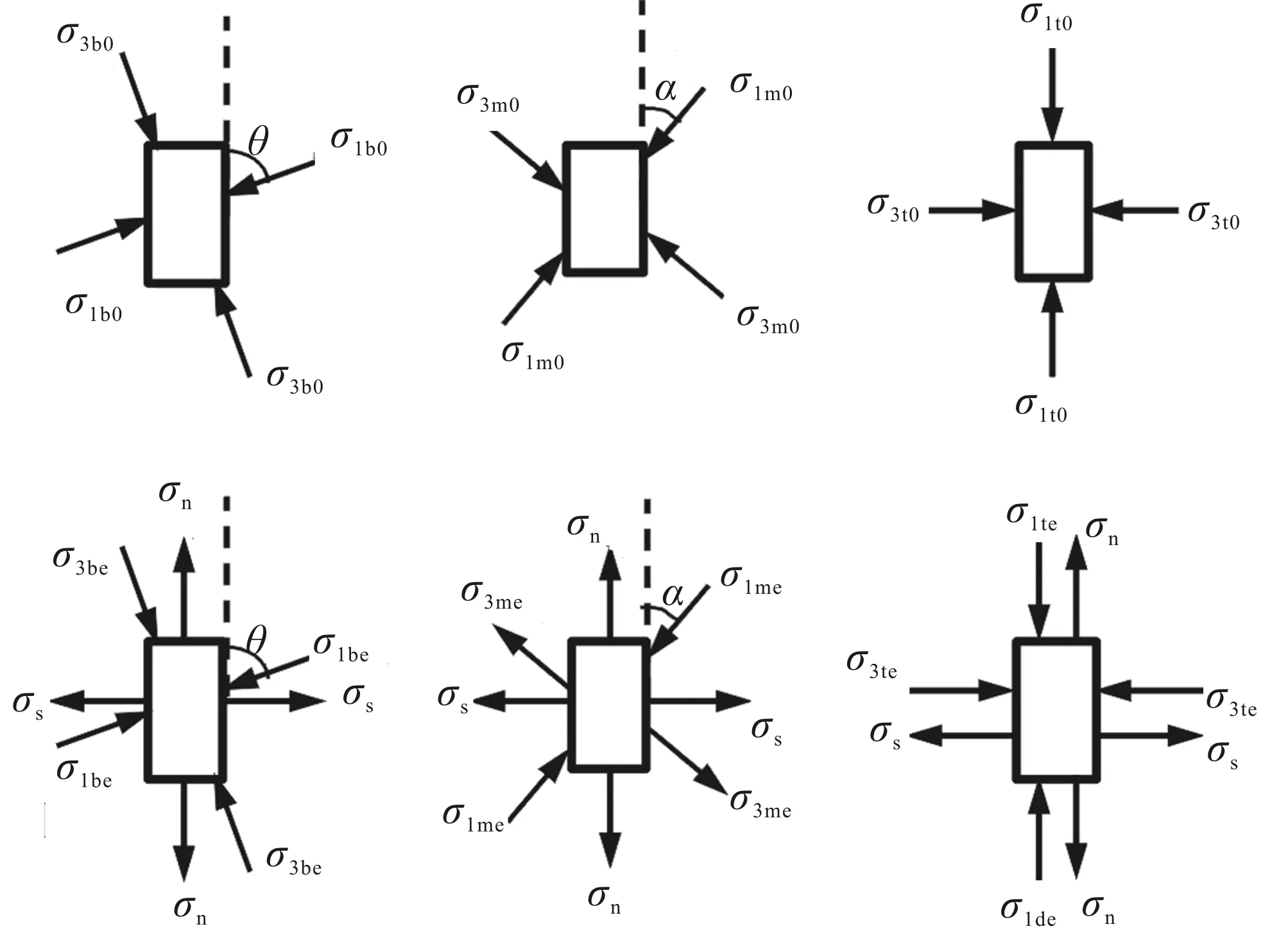
图5　地震作用下边坡失稳前后各段土体应力变化Fig.5　Variation of soil stress in different segments before and after the slope instability under earthquake

考虑到边坡土体应力状态的复杂性，为方便定量计算，假定土体均质且满足摩尔-库伦强度准则，将位于坡面附近土体水平向应力σx定义为与土体埋深z有关的函数[12]:

(5)

式中:K0为侧应力系数；γ为土体重度；β为坡角。

边坡坡顶段(T点)剪应力计算结果为：

(6)

(7)

式中:t=σ3te/σ3t0，0

边坡坡面段(M点)剪应力计算结果为

(8)

(9)

式中:m1=σ1me/σ1m0,m1>1；m3=σ3me/σ3m0,0

边坡坡底段(B点)剪应力计算结果为

(10)

(11)

式中：b1=σ1be/σ1b0,b1>1；b3=σ3be/σ3b0,b3>1；θ为坡底段土体大主应力方向与竖直方向的夹角。

根据以上剪应力计算结果，分别作出三种状态时不同受力段土体的摩尔圆(图6)。从图中可以看出，与无地震作用下边坡失稳时(σ)相比，地震作用下(σe)不同受力部位土体的剪应力受到的影响不同：坡顶段得到较大幅度增长，坡面段呈现小幅增长，坡底段则表现为小幅降低。总体来看，地震作用下边坡失稳过程中剪应力大小及变化趋势表现为：坡顶段初始剪应力较小但增长迅速；坡面段初始剪应力较大且增长较快；坡底段初始剪应力较小且增长较慢。

图6　边坡失稳前后不同滑动段土体剪应力变化Fig.6　Shear stress variation of soil in different segments before and after the slope instability

在地震荷载长持时作用下，边坡土体更容易发生拉破坏[10,13-14]。上述分析中，坡顶段土体受地震作用影响发生因小主应力由压应力转变为拉应力的拉张型剪切破坏，从而较好地解释了地震边坡上部往往呈现出拉破坏特征且存在拉张型裂缝的现象。

1.3黏性土坡三段式滑动地震失稳机制

边坡失稳滑动是由于其内部分土体发生剪切破坏所致，而这种剪切破坏的发生与否则取决于土体的剪应力大小和变化趋势。位于边坡体内不同部位的土体，其受力特点和应力水平本就不同。在边坡失稳前其剪应力水平不同，在边坡失稳过程中，随着应力状态变化的差异，不同位置土体剪应力的变化趋势更是不尽相同。但就土体破坏发展程度而言，剪应力在失稳前原本就大，且在失稳过程中增长快的土体接近破坏的速度更快。

图6所示的地震作用下不同受力段土体剪应力初始水平和变化趋势表明，坡顶段可能同时甚至先于坡面段发生破坏。一些震后顶部存在大量深长拉张型裂缝但整体却未发生失稳的黏性土坡的存在[10,13-14]，也能说明地震作用下此类边坡的失稳可能始于坡顶段的破坏。

综合考虑地震作用下黏性土坡不同受力段应力变化特征和失稳破坏特征，将地震作用以应力的形式表征，以斜坡不同位置土体应力状态及变化来描述斜坡地震失稳的特征，研究提出黏性土坡三段式滑动地震失稳机制：地震作用下，坡顶段受地震拉张作用的影响，侧向支撑力迅速减小从而发生主动土压破坏，形成后缘张裂缝;与此同时，坡面段因无法承受坡顶段下滑土体逐渐增大的推力、自身上覆岩土产生的下滑力和地震惯性力而沿原本就已存在的强度较低的相对软弱带(面)发生蠕动;在坡面段和坡顶段剩余下滑力的推挤下，若坡底段土体不发生破坏，则滑动面在坡面出露，滑体在坡面剪出，若坡底段土体产生被动土压破坏并形成破坏面，则滑动面空间得以完全贯通三段土体，滑坡开始加速整体滑移。

2考虑黏性土坡三段式滑动地震失稳机制的有限元强度折减法

有限元强度折减法是目前较为成熟的边坡地震稳定性分析方法，若要将其与黏性土坡地震三段式滑动失稳机制相结合，则应找寻该方法中与剪应力有关的定义并加以分析和利用。

在有限元强度折减法中，边坡失稳是通过土体强度的折减变低导致土体破坏来实现的。折减系数增幅的大小与土体接近破坏速度的快慢有关。

既然实际边坡失稳时土体应力变化下的剪应力初始大小和变化趋势决定了土体接近破坏的速度，而在有限元强度折减法中土体接近破坏的速度又取决于折减系数的增长速度，因此可以通过对不同受力段折减系数进行调整来实现黏性土坡三段式滑动地震失稳机制和有限元强度折减法的结合。

在运用有限元强度折减法进行边坡地震稳定性分析时，由于不同受力段都在边坡受力达到极限平衡时停止折减，即折减时间相同，所以要满足不同受力段土体接近破坏时速度不同的特征，三段土体的折减系数初值应相等，终值应保证在使边坡受力达到极限平衡状态的前提下，满足坡顶段和坡面段较大、坡底段较小的条件。

3数值模拟验证

运用上述考虑黏性土坡三段式滑动地震失稳机制的有限元强度折减法进行边坡地震稳定性分析，选用定义更为明确合理的斜坡土体位移突变点法，并结合破裂面贯通及计算收敛两种失稳判据来确定边坡动力安全系数[15-16]。

选用具有集合定义和场变量功能的ABAQUS有限元软件，利用其集合定义功能完成对边坡不同受力段的划分，将坡顶段、坡面段和坡底段折减系数ωt、ωm和ωb定义为同一场变量。考虑到坡顶段与坡面段破坏先后顺序难以确定，在保证边坡能够达到极限平衡状态的条件下，分为ωt>ωm>ωb、ωt=ωm>ωb及ωm>ωt>ωb三种情况进行试算。

选取2013年岷县漳县MS6.6地震诱发的永光村西侧滑坡，以验证拓展的有限元强度折减法的可靠性。该滑坡为地震诱发的典型黄土滑坡[17-18]，坡高270m，平均坡度为28.7°，斜坡简化模型如图7所示。根据已有的现场测试和室内土体力学实验结果，滑坡基岩上覆土体分为三层，各层土体物理力学参数如表1所列。土体计算采用理想弹塑性本构模型及莫尔-库仑屈服准则。边坡的有限元分析模型和网格划分如图7所示。模型土体均采用四边形四节点平面应变单元，网格划分为763个单元、837个节点。模型左右边界采用黏弹性边界条件，底部为人工边界。

表 1　各层材料参数

在动力计算过程中，水平向地震荷载从模型底部由左到右输入。输入地震波采用岷县漳县6.6级地震中距震中18km的岷县台记录的主震加速度时程(图8)。其地震峰值加速度为220gal，卓越频谱为4.5～5.5Hz，输入地震动作用时间为40s。

图7　边坡简化模型Fig.7　Simplified model of the slope

图8　地震波加速度时程曲线Fig.8　Acceleration time-history curves of input seismic wave

有限元强度折减法折减系数和水平向位移计算结果如图9所示。折减系数的取值范围为0.5～1.2，当折减系数取1.00时，计算不收敛，边坡达到极限平衡状态，即该边坡以折减系数定义的动力安全系数ωc为1.00。

图9　有限元强度折减法计算结果Fig.9　Results of strength reduction FEM

该拓展方法首先应保证极限平衡状态时各段折减系数的取值范围能够达到原方法所得的折减系数ωc；其次，由于边坡滑动时土体中同时存在残余强度和峰值强度，且前者约为后者的70%～90%[19]，取80%作为极限平衡状态时折减系数变化幅度的上限，即折减系数最大取值不超过1.25ωc。选取符合上述条件，且满足ωt> ωm>ωb、ωt=ωm>ωb及ωm>ωt>ωb三种不同条件的三组折减系数(表2)进行试算。图10为拓展方法折减系数和水平向位移的计算结果，分别画出两种方法得到的折减系数-位移曲线(图11)。采用以边坡土体位移突变点法为主的综合判据法确定边坡动力安全系数，并对两种方法得到的动力安全系数加以分析比较。通过对比不同组计算结果(如表2所列)可以看出：当ωt>ωm>ωb时拓展方法所得动力安全系数较大；当ωt=ωm>ωb时两种方法所得动力安全系数接近；当ωm>ωt>ωb时拓展方法所得动力安全系数较小。

图10　拓展方法计算结果Fig.10　Calculation results using the expanding method

图11　折减系数-边坡顶点水平向位移曲线Fig.11　Relationship between horizontal displacement at the top of slope and reduction factor

该滑坡采用极限平衡法中简化Bishop法计算得到的动力安全系数为0.851，采用瑞典条分法及Janbu法得到的动力安全系数分别为0.891和0.895，拓展后折减系数满足ωt>ωm>ωb条件的有限元强度折减法得到的结果为0.880。该结果显然与极限平衡法得出的结果更为接近，从数值模拟层面验证了黏性土坡三段式滑动地震失稳机制的合理性。

这说明考虑黏性土坡三段式滑动地震失稳机制的动力有限元强度折减法应用于黄土斜坡地震稳定性分析是合理可行的，以其为依据确定的动力安全系数是安全可靠的。

表 2　折减系数及边坡安全系数

4结论

(1) 边坡不同受力段土体剪应力受到地震作用的影响不同：坡顶段得到较大幅度增长，坡面段呈现出小幅增长，坡底段则表现为小幅降低。总体来看，地震作用下边坡失稳过程中剪应力大小及变化趋势表现为：坡顶段初始剪应力较小但增长迅速，坡面段初始剪应力较大且增长较快，坡底段初始剪应力较小且增长较慢。

(2) 结合黏性土坡滑动模式和地震失稳破坏特征，提出了黏性土坡三段式滑动地震失稳机制。地震作用下，坡顶段受地震拉张作用的影响，侧向支撑力迅速减小从而发生主动土压破坏，形成后缘张裂缝。与此同时，坡面段因无法承受坡顶段下滑土体逐渐增大的推力、自身上覆岩土产生的下滑力和地震惯性力而沿原本就已存在的强度较低的相对软弱带(面)发生蠕动。在坡面段和坡顶段剩余下滑力的推挤下，若坡底段土体不发生破坏，则滑动面在坡面出露，滑体在坡面剪出，若坡底段土体产生被动土压破坏并形成破坏面，则滑动面空间得以完全贯通三段土体，滑坡开始加速整体滑移。

(3) 边坡土体剪应力水平及其变化趋势是地震边坡失稳机理与边坡地震稳定性分析方法的重要联系，通过对有限元强度折减法中折减系数进行调整，可以充分体现黏性土坡三段式滑动地震失稳机制。

(4) 考虑黏性土坡三段式滑动地震失稳机制的有限元强度折减法所得的动力安全系数与极限平衡法所得结果十分接近。此方法的提出，实现了地震边坡失稳机理与边坡地震稳定性分析方法的初步结合，为实际工程的黏性土坡地震稳定性分析提供了较为可靠的数值模拟依据。

参考文献(References)

[1]KramerSL.EffectsofEarthquakesonDamsandEmbankmentsGeotechnicalEarthquakeEngineering[M].USA,NewJersey:PrenticeHall,1995.

[2]李天池.地震与滑坡的关系及地震滑坡预测的探讨(节录)[C]//滑坡文集(第二集).北京:中国铁道出版社,1979：127-132.

LITian-chi.DiscussionoftheRelationshipbetweenEarthquakeandtheLandslideandEarthquakeLandslidePrediction(Excerpt)[C]//LandslideAnthology(SecondVolume).Beijing:ChinaRailwayPublishingHouse,1979:127-132.(inChinese)

[3]祁生文,伍法权, 刘春玲,等.地震边坡稳定性的工程地质分析[J].岩石力学与工程学报,2004,23(16):2792-2797.

QISheng-wen，WUFa-quan,LIUChun-ling,etal.EngineeringGeologyAnalysisonStabilityofSlopeunderEarthquake[J].ChineseJournalofRockMechanicsandEngineering,2004,23(16):2792-2797.(inChinese)

[4]张振中.黄土地震灾害预测[M].北京:地震出版社, 1999.

ZHANGZhen-zhong.TheEarthquakeDisasterPredictioninLoessAreas[M].Beijing:SeismologicalPress,1999.(inChinese)

[5]TerzaghiK.MechanismsofLandslides,EngineeringinGeology(Berdey)Volume[M].US:GeologicalSocietyofAmerica,1950.

[6]NewmarkNM.EffectsofEarthquakesonDamsandEmbankments[J].Geotechnique,1965,15(2):139-160.

[7]刘红帅,薄景山,刘德东.岩土边坡地震稳定性分析研究评述[J].地震工程与工程振动,2005,25(1):164-171.

LIUHong-shuai,BOJing-shan,LIUDe-dong.ReviewonStudyofSeismicStabilityAnalysisofRock-soilSlopes[J].EarthquakeEngineeringandEngineeringVibration,2005,25(1):164-171.(inChinese)

[8]叶海林,黄润秋,郑颖人.地震作用下边坡稳定性安全评价的研究[J].地下空间与工程学报,2009,5(6):1248-1257.

YEHai-lin,HUANGRun-qiu,ZHENGYing-ren.TheStudyofSafetyEvaluationonSlopeSeismicStability[J].ChineseJournalofUndergroundSpaceandEngineering,2009,5(6):1248-1257.(inChinese)

[9]陈仲颐,周景星,王洪瑾.土力学[M].北京:清华大学出版社,2004.

CHENZhong-yi,ZHOUJing-xing,WANGHong-jin.SoilMechanics[M].Beijing:TsinghuaUniversityPress,1994.(inChinese)

[10]言志信,张森,张学东,等.地震边坡失稳机理及稳定性分析[J].工程地质学报,2010,18(6):844-850.

YANZhi-xin,ZHANGSen,ZHANGXue-dong,etal.FailureMechanismandStabilityAnalysisofSlopeunderEarthquake[J].JournalofEngineeringGeology,2010,18(6):884-850.(inChinese)

[11]王恭先.滑坡学与滑坡防治技术[M].北京:中国铁道出版社,2004.

WANGGong-xian.LandslideandLandslideControlTechnology[M].Beijing:ChinaRailwayPublishingHouse,2004.(inChinese)

[12]王国体.以土体应力状态计算边坡安全系数的方法[J].中国工程科学,2006,8(12):80-84.

WANGGuo-ti.TheMethodandFormulaforStabilityFactorofSlopewithStateofSoilOriginalStress[J].EngineeringScience,2006,8(12):80-84.(inChinese)

[13]郑颖人,叶海林,黄润秋.地震边坡破坏机制及其破裂面的分析探讨[J].岩石力学与工程学报,2009,28(8):1714-1723.

ZHENGYing-ren,YEHai-lin,HUANGRun-qiu.AnalysisandDiscussionofFailureMechanismandFractureSurfaceofSlopeunderEarthquake[J].ChineseJournalofRockMechanicsandEngineering,2009,28(8):1714-1723.(inChinese)

[14]钟秀梅,王谦,张国信,等.天水市水眼寨滑坡特征及稳定性分析[J].地震工程学报,2014,36(4):887-891.

ZHONGXiu-mei,WANGQian,ZHANGGuo-xin,etal.CharacteristicsandStabilityAnalysisofShuiyanzhaiLandslideinTianshuiCity[J].ChinaEarthquakeEngineeringJournal,2014,36(4):887-891.(inChinese)

[15]郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,23(19):3381-3388.

ZHENGYing-ren,ZHAOShang-yi.ApplicationofStrengthReductionFEMinSoilandRockSlope[J].ChineseJournalofRockMechanicsandEngineering,2004,23(19):3381-3388.(inChinese)

[16]雷天,吴志坚,陈拓.天水市某典型黄土边坡块石支护稳定性效果分析[J].地震工程工程学报,2014,36(4):968-974.

LEITian,WUZhi-jian,CHENTuo.StabilityAnalysisofaTypicalLoessSlopeSupportedbyBlockStoneRetainingWallinTianshui[J].ChinaEarthquakeEngineeringJournal,2014,36(4):968-974.(inChinese)

[17]WUZhi-jian,SUNJun-jie,CHENYu-jin,etal.AnalysisofDisaster-causingMechanismofLoessLandslidesInducedbytheMinxian-ZhangxianMS6.6Earthquake,China[C]//Proceedingof6thChina-JapanGeotechnicalSymposium,Hokkaido,2015.

[18]车爱兰,吴志坚,彭冬,等.黄土斜坡震害面波勘探调查及其动力稳定性分析——以甘肃岷县、漳县MS6.6地震为例[J].地震工程学报,2013,35(4):724-729.

CHEAi-lan,WUZhi-jian,PENGDong,etal.SurfaceWaveInvestigationandDynamicStabilityAnalysisforEarthquake-inducedLoessLandslides[J].ChinaEarthquakeEngineeringJournal,2013,35(4):724-729.(inChinese)

[19]谭文辉,任奋华,苗胜军.峰值强度与残余强度对边坡加固的影响研究[J].岩土力学,2007,28(增刊):616-618.

TANWen-hui,RENFen-hua,MIAOSheng-jun,etal.InfluenceofParametersofPeakStrengthandResidualStrengthontheReinforcementofSlopes[J].RockandSoilMechanics,2007,28(Supp):616-618.(inChinese)

EarthquakeInstabilityMechanismofCohesiveSoilSlopeandItsApplicationinSeismicStabilityAnalysisofLoessSlope

ZHAOWen-chen1,WUZhi-jian1,2,CHENYu-jin1

(1.Key Laboratory of Loess Earthquake Engineering, Lanzhou Institute of Seismology, CEA, Lanzhou 730000, Gansu, China;2. Geotechnical Disaster Prevention Engineering Technology Research Center of Gansu Province, Lanzhou 730000, Gansu, China)

Abstract：Based on the earthquake instability characteristics of cohesive soil slopes, in this study, we used the stress analysis method to analyze the process of slope instability. By analyzing the stress state and shear stress variation features of soil in different parts of the slope during earthquakes, combined with the failure characteristics of actual slopes during earthquakes, we developed our proposed three-segment sliding instability mechanism of cohesive soil slopes. From our analysis results of the stress correlation between the above-mentioned mechanism combined with the strength reduction finite element method (FEM), we carried out a dynamic stability analysis of an actual loess seismic landslide. A comparison of our results with those of other methods reveals that the dynamic safety factor obtained by the strength reduction FEM, which considers the three-segment sliding instability mechanism of cohesive soil slopes, was very close to that determined by the limit equilibrium method.

Key words：sliding instability mechanism of cohesive soil slope; seismic stability analysis of slope; strength reduction FEM

收稿日期：①2015-12-31

基金项目：国家自然科学基金资助项目(41472297，51478444)；青海省交通建设科技项目“铁路建设对雅丹地貌的环境影响与减轻技术研究”

作者简介：赵文琛(1991-)，男，硕士，主要从事岩土地震工程方面的研究。E-mail：wenchenzhao1219@126.com。 通信作者：吴志坚(1974-)，男，安徽安庆人，博士，研究员，主要从事岩土地震工程与冻土工程领域的研究。E-mail：zhijianlz@163.com。

中图分类号:TD853.34

文献标志码：A

文章编号:1000-0844(2016)03-0452-08

DOI:10.3969/j.issn.1000-0844.2016.03.0452