基于点模式分析的地质灾害集聚特征及空间热点研究

姚艳豪, 王志宇， 马　品,2, 过仲阳

(1.华东师范大学 地理信息科学教育部重点实验室, 上海　200241; 2.云南省地图院, 云南 昆明　650034)

基于点模式分析的地质灾害集聚特征及空间热点研究

姚艳豪1, 王志宇1， 马品1,2, 过仲阳1

(1.华东师范大学 地理信息科学教育部重点实验室, 上海200241; 2.云南省地图院, 云南 昆明650034)

摘要:以保山市隆阳区为研究区,选取滑坡、泥石流和不稳定斜坡3种典型地质灾害类型为对象,综合运用GIS技术与多种空间点模式分析方法对地质灾害的集聚特征进行定量分析,并划定其空间集聚热点区域．研究结果表明: 隆阳区内滑坡、泥石流和不稳定斜坡灾害均呈显著的空间集聚特征,且集聚程度和规模随观测尺度的变化而变化;各地质灾害的空间集聚特征差异明显,形成了不同的空间集聚模式;不同地质灾害类型在空间热点分布上差异与共生现象并存. 管理者在灾害治理工作中需采用区别治理与统一治理相结合的综合治理方案．

关键词:空间点模式分析; 地质灾害; 集聚; 空间热点; GIS

0引言

地质灾害是在自然或者人为因素的作用下形成的,对人类生命财产、环境造成破坏和损失的地质作用或现象,包括滑坡、泥石流、塌陷、崩塌、不稳定斜坡等多种类型[1,2]．地质灾害在空间上的分布看似“杂乱无章”,但由于致灾因子分布的规律性,使地质灾害存在空间集聚现象,具体表现为地质灾害的多发地段和灾害集群[3]．因此,对地质灾害的空间集聚特征展开研究,并划定其空间集聚热点区域,不仅有助于管理者进行灾害集中治理和灾害防治资源的合理分配,而且能够为地质灾害空间分布格局的相关研究提供一条新思路．

地质灾害可以抽象为地理空间上的点状“事件”,因此可以采用空间点模式分析方法对地质灾害的空间分布模式和集聚特征进行定量研究．空间点模式分析是一种针对点状地理实体或事件的空间分布特征和模式研究方法[4]．空间点模式分析的基本问题是空间点分布的聚集性和分散性问题,其重点在于探测点状“事件”在空间上的分布模式是集中或是离散[5,6]．近年来,点模式分析广泛应用于产业布局、生态学、公共卫生、犯罪学等领域中点状地理实体或事件的集聚特征研究中[7-9]．

在深入分析空间点模式分析方法在各领域中应用案例的基础上,本文将空间点模式分析方法引入到地质灾害空间集聚特征及空间热点研究中，以云南省保山市隆阳区为研究区,针对当地滑坡、泥石流、不稳定斜坡3种典型地质灾害类型,综合运用GIS技术和Ripley′sL函数、核密度估计法、最临近距离层次聚类法等空间点模式分析方法,定量分析研究区域地质灾害空间集聚模式及特征,确定空间集聚热点区域,以期为管理者提供一种高效的地质灾害防治方法．

1研究区概况与数据

1.1研究区概况

选择云南省保山市隆阳区作为研究区域．隆阳区(24°46′～25°38′N,98°43′～99°26′E)位于云南省西部山区,全区土地总面积约4 855.51 km2,其中山区、半山区占总面积的92.6%．本区东北隔澜沧江与大理相望,南和保山市的施甸、龙陵县相连,西以高黎贡山脊与腾冲县为界,北顺怒江而上与怒江傈僳族自治州毗邻,下辖2个街道、6个镇、6个乡、4个民族乡,298个行政村．隆阳区地理位置如图1所示．

隆阳区全境地势大体呈北高南低之势,地形起伏较大,地形切割众多,地质地貌结构非常复杂．复杂多变的地理环境和剧烈的人类活动导致区内地质灾害频发,是云南省地质灾害的易发区和高发区之一,地质灾害防治任务十分艰巨．境内灾害类型主要包括滑坡、泥石流、崩塌、不稳定斜坡等．

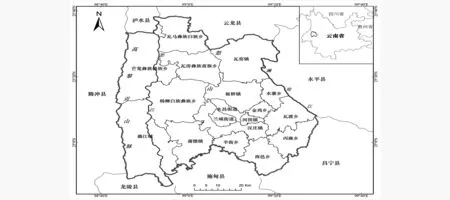
图1　研究区地理位置示意图

1.2数据来源

地质灾害数据来源于全国第一次地理国情普查数据．该项普查是由国务院于2013～2015年期间主持开展的一项重大国情国力调查,其普查对象是我国陆地国土范围内的地表自然和人文地理要素,其目的是全面获取地理国情信息,掌握地表自然、生态以及人类活动的基本情况[11]．

地质灾害数据包含隆阳区内历次地质灾害点位及其他灾情详细信息,共298处,其中大型灾害18处,中型灾害58处,小型灾害222处,分散在全区17个乡镇(街道),涉及滑坡、泥石流、不稳定斜坡、崩塌等6种地质灾害类型．表1为隆阳区各地质灾害类型的基本统计信息．

表1　隆阳区各地质灾害类型基本统计信息表

由表1可见,滑坡、不稳定斜坡和泥石流是隆阳区地质灾害的3种主要地质灾害类型．鉴于此,主要针对这3种典型的地质灾害类型展开研究．研究区内滑坡、不稳定斜坡与泥石流空间分布图如图2．

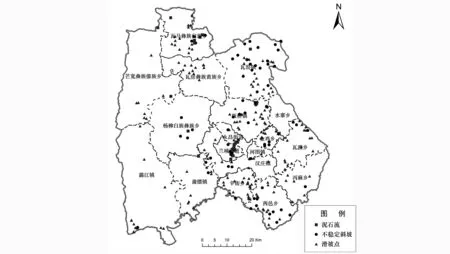
图2　研究区地理位置及历史地质灾害点分布图

2研究方法

Ripley′sL函数、核密度估计法和最邻近层次聚类法是用于检测空间点分布模式的几种常用统计学方法．一方面,Ripley′sL函数可以最大限度地利用空间点信息,从多个尺度上研究地质灾害的空间集聚特征,反映其空间聚集模式在多个空间尺度下的变化情况[12];另一方面,核密度估计法可以从相关或类似的邻近小地域借助信息,建立数学模型将获得的小地域数据综合起来,对本地域的参数进行修匀,以减少样本含量小,数据不稳定的影响[13],最邻近层次聚类法则能进一步从多个级别划定集聚热点区域．

因此,将地质灾害抽象为地理空间上的点状“事件”,运用Ripley′sL函数对来连续空间上地质灾害的空间集聚模式及集聚特征进行定量研究,进而运用核密度估计法通过点密度变化的形式对研究区内各类地质灾害的空间分异状况进行平滑显示,然后运用最邻近距离层次聚类法划定多层次的集聚热点区域,从而为地质灾害的等级化重点治理提供依据．

2.1Ripley′s L函数

Ripley′sL函数是Ripley′sK函数最常见的一种变体．Ripley′sK函数是一种以分散性为基础的基于距离的空间点模式分析方法[9]．它主要用于定量评估某一距离范围内点状要素的空间分布模式,是聚集或是离散[14]．Ripley′sK函数的计算方法是:首先定义一个空间距离尺度d,分别以各个地质灾害点为圆心,d为半径定义搜索圆,并统计落入圆内灾害点数量,然后计算落入该搜素圆内灾害点数量的数学期望与研究区地质灾害点总体分布密度之间的比值,分别对不同的d值重复上述过程．

Ripley′sK函数可以表示为:

(1)

因此,Ripley′sK函数可以转化为以下形式:

(2)

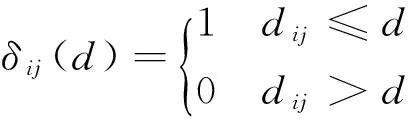
(3)

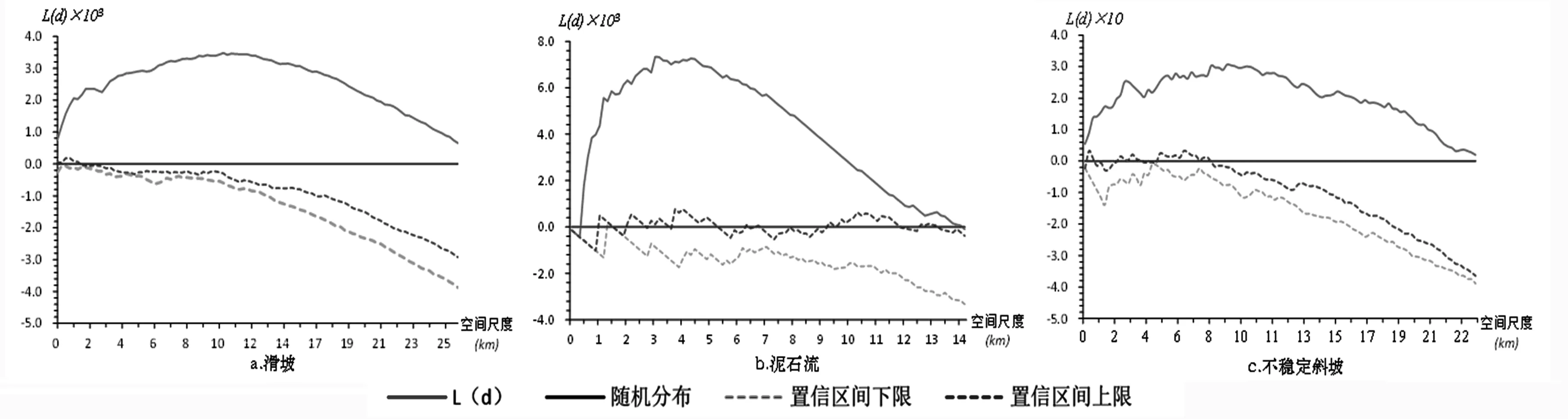
通过绘制L(d)与空间尺度d的关系曲线(图3),定量测度不同空间尺度下的地质灾害的空间分布模式．在随机分布的假设下,L(d)的期望值为0．若L(d)=0,地质灾害服从随机分布;若L(d)>0,地质灾害呈聚集分布特征,且L(d)值越大,集聚程度越高;若L(d)<0,则地质灾害呈均匀分布[16]．

Ripley′sL函数一般采用蒙特卡罗法(MonteCarlo)检验点事件空间分布模式的显著性[17]．通过随机模拟运算,得到L(d)函数的置信区间上限L(d)max和下限L(d)min．若L(d)>L(d)max,表明地质灾害呈显著空间集聚分布;若 L(d)min

图3　Ripley′s L函数曲线

2.2核密度估计法

核密度估计法通过考察规则区域中点密度的空间变化来研究点的分异特征[19],它适用于以可视化方式表示空间点分布模式,从而实现对点状“事件”在连续空间下的集聚与分散情况的平滑表示[20]．

核密度估计法一般通过测度研究区域内单位面积上的事件数来估计某点的密度．以某地质灾害点p为圆心,通过设定半径(带宽)h,统计该圆形范围内地质灾害点数目,然后除以圆面积．因此,地质灾害点p处的密度λh(p)可以表示为如下形式:

(4)

其中:K为核函数;p为地质灾害点集{p1,p2,…,pn};h代表带宽;pi为落在以点p为圆心,以h为半径的圆形范围内的第i个地质灾害点的位置.有研究表明:在带宽h确定的前提下,核函数的选择对核密度估计的结果影响并不大[21]．选择高斯核函数进行密度估计,其表达式如下:

(5)

由此可见带宽h的选择直接决定了核密度估计的平滑程度,它是核密度估计方法的关键．带宽越小,密度估计结果的细节变化信息越丰富;带宽越大,密度估计结果的细节信息减少,小的集聚热点区域将被合并成大的热点,空间上密度变化更光滑,可视化效果更好[22]．通过经验法确定带宽h,即通过选取多个h值进行密度估计试验,并观察密度估计结果,进而选择最优带宽值．

2.3最临近距离层次聚类法

最邻近距离层次聚类法(Nearest Neighbor Hierarchical Cluster)是一种通过最邻近分析技术识别最小数量的自定义点集合,从而有效地划定点状地理实体的空间分布热点的统计分析方法[23]．

运用该方法探索研究区域内的各类地质灾害的空间集聚热点位置．首先定义一个聚集单元最大距离阈值作为聚集规则,然后与每个地质灾害点对的距离进行比较,当某一点与其他点的距离小于最大距离阈值时,则将该点计入聚集单元．据此将原始地质灾害点聚集为若干个集聚区域,称为一阶(First-Order)热点区域．利用同样方法,对一阶热点区域进行二次聚类,可以得到二阶(Second-Order)热点区域．以此类推,理论上直到所有点呈一个集合或条件失败为止[15,24,25],最终得到研究区内不同层次的地质灾害空间热点区域．

有研究表明:最邻近距离层次聚类法的聚集规则也可以通过每个簇集包含的最小点数(Minimun points per cluster)来定义[26,27]．最邻近距离层次聚类法分析结果直接受最大距离阈值或簇集最小点数的影响,因此如何确定最大距离阈值或簇集最小点数是本方法的关键．选用簇集最小点数作为聚类规则,将簇集最小点数设为2～10之间的数字,并采用随机最邻近距离作为最大距离阈值,借助CrimeStat软件的最邻近距离层次聚类工具进行最邻近距离层次聚类试验,最终选定簇集最小点数为3时,聚类效果达到最佳．需要指出的是,此处的空间热点区域只是一个相对概念,即相对于区域内其他地区在地质灾害频次和密度上具有明显优势的地区,空间热点区域并不一定发生灾害,而非空间热点区域仍有可能发生灾害[28]．

3结果与分析

3.1地质灾害空间集聚特征

运用CrimeStat 3.3软件工具中的Ripley′sK函数分析模块,分别对研究区内滑坡、泥石流、不稳定斜坡3种地质灾害类型的空间集聚模式及集聚特征进行定量分析,并利用蒙特卡罗法对计算结果进行了随机模拟检验(100次,95%)．最后将运算结果导入Excel,绘制Ripley′sL函数与空间距离尺度的关系曲线(图4)．表2为滑坡灾害Ripley′sL函数部分运算结果．

表2　Ripley′s L函数运算结果统计表(滑坡)

图4　研究区各类地质灾害分布的Ripley′s L函数曲线

从图2中可以发现: 3种地质灾害随空间距离尺度的变化呈现不同的空间集聚模式和集聚强度．滑坡与不稳定斜坡的L(d)值均大于0,且Ripley′sL函数曲线均位于置信区间上限曲线的上部,全部通过显著性检验,表明在所有观测距离尺度下,这两种地质灾害均呈显著的空间集聚性;对于泥石流灾害,当空间距离尺度d<0.4 km或d>14.5 km时,L(d)<0,此时泥石流呈均匀分布;而空间距离尺度d在[0.4 km,14.5 km]之间,泥石流灾害呈显著的空间集聚特征．

进一步对Ripley′sK函数曲线图分析发现: 1) 从L(d)曲线的变化趋势来看,3种地质灾害的聚集程度随着观测尺度d的增大均呈“先增强后减弱”的特征,且滑坡与不稳定斜坡的L(d)曲线轨迹具有相似性．这可能是由于两种灾害在形成机制上相似,滑坡是不稳定斜坡的子门类造成的,同时也间接地证明了灾害诱发因素在空间上的集聚与规律性是形成灾害集聚特征的主要因素; 2) 各地质灾害类型集聚规模与强度具有明显差异,形成不同的空间集聚模式．从灾害集聚规模与强度上来看,滑坡、泥石流与不稳定斜坡的L(d)值首个峰值分别为3 500,7 300和3 100,其对应的观测距离分别为10.7,3.2和8.6 km．数据表明, 3种地质灾害的集聚规模和强度存在明显差异．泥石流的集聚强度最大,滑坡次之,不稳定斜坡最小;而在集聚规模方面,滑坡最大,其次是不稳定斜坡,泥石流的集聚规模最小．

地质灾害类型在空间上大体可分为3种集聚模式:“大分散、小集聚”模式,“大分散、大集聚”模式,“小分散、大聚集”模式[29]．其中,滑坡灾害分布广泛,热点区域众多,集聚规模与集聚强度均较高,属“大分散、大集聚”模式;泥石流灾害分布相对集中,集聚强度大,但集聚规模上最小,属“小分散、大集聚”模式;不稳定斜坡分布相对均衡,但集聚强度小,属“大分散、小集聚”模式．

3.2地质灾害空间分异特征及集聚热点分析

为了进一步探寻研究区内各地质灾害类型空间分异状况和空间集聚热点区域的详细位置,运用核密度估计法和最邻近距离层次聚类法分析3种地质灾害的空间分异情况,并划定其多层次的空间集聚热点区域(图5),统计各地质灾害类型空间集聚热点区域的位置(表3)．

表3　各地质灾害类型空间集聚热点区域

图5　研究区地质灾害空间热点区域分布

从总体上来看,隆阳区内地质灾害空间分布呈现以下特点:

1) 隆阳区内地质灾害主要分布于隆阳区北部和东南部(怒山东侧)广大地区,而隆阳区西部芒宽镇、潞江镇、杨柳乡等地区地处高黎贡山脉东麓,地形复杂,但人类活动较少,因此地质灾害密度较小,说明人类工程活动的影响是地质灾害的重要因素．另外,兰城街道、永昌街道中部地区,由于位于怒山与保山盆地交界区域,地形复杂、且人类活动强烈,是3种地质灾害的公共热点区域,受各种地质灾害综合影响,且危害对象为保山城区,应引起特别重视．

2) 3种地质灾害类型均存在明显的空间集聚热点区,从而为地质灾害的区域重点防治提供了依据．滑坡灾害集聚热点区域在数量和规模上均大于泥石流与不稳定斜坡灾害,并在形成多处一阶集聚热点区域的基础上,形成了瓦马南部-瓦房北部、板桥东部-瓦窑东南部两大二阶集聚区．而泥石流灾害规模最小,然而分布最为集中．

3) 不稳定斜坡的空间热点与滑坡灾害的集聚热点区域存在部分重合,说明了两者经常同时发生,进一步印证了两者在灾害形成机制上的相似关系．

从分灾害类型来看,地质灾害类型的空间分异特征和集聚热点分布存在明显差异．滑坡灾害分布范围较广,集聚热点区域众多,主要分布于隆阳区北部、怒山东部区域、保山盆地周围及澜沧江沿岸地区;泥石流灾害规模最小,集中于瓦马乡东部及永昌街道-兰城街道中部地区;不稳定斜坡与滑坡灾害分布区域相似,由于灾害形成机制的联系,因此两者经常伴随发生．

4结论与展望

4.1结论

将地质灾害抽象为地理空间上的点状“事件”,采用空间点模式分析方法来对地质灾害的空间集聚模式和空间集聚热点区域展开研究．Ripley′sL函数、核密度估计法和最邻近距离层次聚类法是3种典型的空间点模式分析方法,在分析地质灾害空间集聚特征及集聚热点区域方面有其独特的优势．Ripley′sL函数可以研究多个空间距离尺度上地质灾害空间集聚特征,分析其空间集聚规模与强度随不同空间尺度的变化情况．核密度估计法对地质灾害的空间分异状况进行平滑显示. 最邻近距离层次聚类法则进一步划定多个级别的集聚热点区域,从而为地质灾害的等级化重点治理提供依据．

以2013～2015年开展的地理国情普查数据为基础,综合运用GIS技术和Ripley′sL函数、核密度估计法及最邻近距离层次聚类法等多种空间点模式分析方法对隆阳区内滑坡、泥石流及不稳定斜坡灾害的空间集聚特征与集聚热点区域展开了重点分析．研究结果显示:

1) 地质灾害虽然表面上看起来是彼此毫无关联的“独立事件”,在宏观上却遵循一定的规律,呈现显著的空间集聚特征．

2) Ripley′sL函数分析表明,地质灾害空间分布模式和集聚强度对空间距离尺度具有很强的依赖性,即地质灾害空间随着空间尺度的变化可能呈现不同的空间分布模式或集聚强度．

3) 由于地质灾害之间的形成机制存在差异与联系,不同地质灾害类型的空间集聚特征存在明显差异,因此管理者不仅需要对差异明显的地质灾害类型进行区别治理,同时需要探索不同地质灾害的是否存在共生现象,以便制定高效的治理方案．

4) 最邻近层次聚类分析结果表明,各地质灾害类型均存在明显的空间集聚热点区域,且集聚热点区域的数量和规模存在差异,可根据集聚热点区域,对地质灾害进行“定点式”治理．

本文定量测度了不同空间尺度下研究区内各地质灾害类型的空间集聚模式及集聚规模与强度,并划定了多级集聚热点区域,一方面可以给相关管理部门进行灾害重点防治决策和合理调配部署资源提供理论依据;另一方面,也为地质灾害的集聚特征及空间热点研究提供了一条新思路,为空间点模式分析方法在灾害防治领域的后续研究起到“抛砖引玉”的作用．

4.2展望

利用空间点模式分析方法对地质灾害的空间集聚特征研究仍处于初步探索阶段,尚存在诸多未涉及到的问题,有待进一步探讨．例如自然条件、人类工程活动等因素对地质灾害空间集聚特征的影响及相互关系、空间热点区域的划分在地质灾害防治中的具体应用以及地质灾害集聚特征在不同时间尺度上的扩展研究等问题．

参考文献：

[1]张良弼.地球科学大辞典:应用学科卷[M].北京:地质出版社,2005:487.

[2]眭素刚.云南省宾川县地质灾害危险性区划评价研究[D].昆明:昆明理工大学,2007.

[3]邱海军,曹明明,刘闻,等.区域地质灾害的空间点格局分析研究——以宁强县为例[J].干旱区资源与环境,2014,28(3):107-111.

[4]佘冰,朱欣焰,呙维,等.基于空间点模式分析的城市管理事件空间分布及演化——以武汉市江汉区为例[J].地理科学进展,2013,32(6):924-931.

[5]杜世宏.多尺度空间关系理论与实践[M].北京:科学出版社, 2014.

[6]杨瑞霞.中原地区史前聚落分布空间分布空间模式研究[D].郑州:河南工业大学,2010.

[7]张金屯,孟东平.芦芽山华北落叶松林不同龄级立木的点格局分析[J].生态学报,2004,24(1):35-40.

[8]迟文学,王劲峰,李新虎,等.出生缺陷的空间点格局分析[J].环境与健康杂志,2007,24(4):238-241.

[9]王丽,曹有挥,刘可文,等.高铁站区产业空间分布及集聚特征——以沪宁城际高铁南京站为例[J].地理科学,2012,32(3):301-307.

[10]Beato Filho C C,Assuno R M,Silva B F A d,et al.Homicide clusters and drug traffic in Belo Horizonte,Minas Gerais State,Brazil from 1995 to 1999[J].Caderons de Sau de Pu blica,2001,17(5):1163-1171.

[11]王本洋,余世孝,王永繁.种群分布格局的各向异性分析[J].中山大学学报:自然科学版,2006,45(2):83-87.

[12]王功军,骆福添.核估计在小地域分析疾病中的应用[J].中国医院统计,2005,12(3):231-233.

[13]Okabe A,Yamada I.The K-function method on a network and its computational implementation[J].Geographical Analysis,2001,33(3):271-290.

[14]Besag J E.Comments on ripley's paper.Journal of the Royal Statistical Society[J]. Journal of Geographical,2013,68(4):464-475.

[15]方忠权.广州会展企业空间集聚特征与影响因素[J].地理学报,2013,68(4):464-475.

[16]Okabe A,Yamada I.The K-function method on a network and its computational implementation[J].Geographical Analysis,2001,33(3):271-290.

[17]湛东升,孟斌.基于社会属性的北京市居民居住与就业空间集聚特征[J].地理学报,2013,68(12):1607-1618.

[18]王远飞, 何洪林.空间数据分析方法.北京:科学出版社,2007

[19]Berke O. Exploratory disease mapping:Kriging the spatial risk function from regional count data[J]. International Journal of Health Geography, 2004, 3(1): 18-22.

[20]Xie Z X,Yan J.Kernel density estimation of traffic accidents in a network space[J].Computers,Environment and Urban Systems,2008,32(5):396-406.

[21]佘冰,朱欣焰,呙维,等.道路网约束下的城市事件空间点模式分析[J].计算机应用研究.2013,30(8):2327-232.

[22]汪兰香.福州城市犯罪制图及其空间分析[D].福州:福建师范大学,2012.

[23]John E E,Spencer C,James G C,et al. Mapping crime:understanding hots pot[M].Washington: National Institute of Justice,2005.

[24]秦波. 上海市产业空间分布的密度梯度及影响因素研究[J].人文地理, 2011, 26(1):39-43.

[25]朱丽霞,杨婷,郑文生.武汉市生产性服务业空间特征及其发展演变[J].地域研究与开发,2014,33(2):73-76.

[26]高杰,王志强,邵琦,等.Ripley’sL指数与最近邻空间热点分析在流行病学标点地图分析中的应用[J].山东大学学报:医学版,2009,47(3):89-93.

[27]郭福涛,胡海清,马至海.应用空间点模式方法研究大兴安岭雷击火空间分布格局[J].生态学报,2009,29(12):6742-6747.

[28]张景秋,陈叶龙.北京城市办公空间的行业分布及集聚特征[J].地理学报,2011,66(10):1299-1308.

[29]国务院.国务院关于开展第一次全国地理国情普查的通知国发(2013)9号[EB].http://www.gov.cn/zwgk/2013-03/05/content-2346074.htm,2013-03-05.

[责任编辑：蒋海龙]

Study on Spatial Clustering Characteristics and Spatial Hot Spot of
Geological Disaster based on Spatial Point Pattern Analysis
YAO Yan-hao1, WANG Zhi-yu1, MA Pin1,2, GUO Zhong-yang1

(1.Key Laboratory of Geographic Information Science of Ministry of Education, East China Normal University,Shanghai 200241, China)

(2.Map Hosital of Yunnan Province, Yunnan Kunming 650034, China)

Abstract:By examining the spatial clustering characteristic of geological disaster and demarcating the corresponding spatial hot spot,we can provide important support for making sound decisions on geographical disaster prevention and allocation of disaster prevention resources.Taking Longyang district,Baoshan city as study area, landslide and debris flow, unstable slope of 3 kinds of typical geological disaster was selected as study targets,this article combine GIS technology with a variety of spatial point pattern analysis method to study on the spatial clustering characteristics and spatial hot spots of geological disasters. Conclusions are drawn as follows: Generally speaking, landslide and debris flow, unstable slope in study area are significantly agglomerated, and the agglomeration degree changing with the spatial scale; spatial agglomeration of each geological disaster presented different characteristics,different spatial clustering patterns was formed. From the perspective of spatial clustering hot spots, there are both symbiosis phenomenon and different hot spots among different geological disasters.Therefore,the manager department should make a comprehensive treatment plan which is combined differential treatment with comprehensive harnessing.

Key words:spatial point pattern analysis; geological disaster; cluster; spatial hot spot; GIS

收稿日期:2015-11-12

基金项目:国家自然科学基金资助项目(J1310028)

通讯作者:过仲阳(1965-),男,浙江嵊县人,教授,博士生导师,主要从事遥感影像处理、虚拟地理环境与数据挖掘等研究．

中图分类号:X43

文献标识码:A

文章编号:1671-6876(2016)01-0043-08

E-mail: zyguo@geo.ecnu.edu.cn