非合作博弈下功率与速率联合控制算法研究

余　翔，张小银

(重庆邮电大学 通信与信息工程学院，重庆 400065)



非合作博弈下功率与速率联合控制算法研究

余翔，张小银

(重庆邮电大学 通信与信息工程学院，重庆 400065)

摘要：针对已有的基于非合作博弈的功率控制算法中认知用户公平性的不足，提出了对认知用户的发射功率和传输速率进行联合控制的算法，在代价函数中设计了基于传输速率公平性的惩罚因子，同时还考虑了认知用户受到的干扰，与固定认知用户传输速率的功率控制算法进行仿真对比表明，在对认知用户发射功率进行调整的同时，通过调整认知用户的传输速率，能使认知用户在传输速率的分配上与目标传输速率的距离更小，更加体现了认知用户之间的公平性。

关键词：博弈论；功率控制；速率控制；公平性

0前言

认知无线电技术在提高频谱资源的利用率方面发挥了巨大作用，它是在软件无线电基础上发展起来的，但是两者又有着本质的区别，认知无线电的思想是利用具有认知功能的无线通信设备主动搜索授权用户未用或者很少使用的频段，通过调整自身参数(工作频率，调制方式，发射功率和通信协议等)去适应周围环境，在时间和空间上充分利用空闲频谱，以此来提高频谱资源的利用率[1]。

认知用户使用授权频段的方式主要有[2]：开放式频谱共享，择机式频谱共享和协商式频谱共享。在择机式频谱共享的下垫式接入方式[3]中，认知用户在满足一定的标准下和授权用户在同一时间共享频段，因为授权用户对授权频段享有绝对的优先权，这就要求认知用户不能对授权用户的正常通信造成干扰，这就需要对认知用户的发射功率进行控制来降低对授权用户的干扰[4]。将博弈论[5]工具应用到功率控制技术中已经得到了广泛认可，文献[6]提出了一种基于归一化效用函数的功率控制算法，让认知用户在不影响授权用户使用频谱的前提下，保证了自身的通信质量，但是在大型蜂窝网络中，基于对多业务的考虑，不同的业务有不同的需求，对语音数据的传输注重的是时延，但是对数据业务的传输则更加看重误码率，这就需要为不同需求的用户提供灵活的功率服务，在对认知用户的发射功率进行控制的同时还要根据需要对认知用户的传输速率进行控制，文献[7]提出了基于非合作博弈的联合速率和功率控制算法模型；文献[8]引入了简单的线性代价函数；文献[9]在代价函数中考虑了传输时延，保证了认知用户在进行通信时有较低的时延；文献[10]加入了对传输速率的控制，改善了认知用户的服务质量 (quality of service，QoS)，但是他们都没有考虑到认知用户受到的干扰。本文基于公平性的原则，对认知用户的传输速率和发射功率进行联合控制，提出了基于传输速率的惩罚因子，在不对授权用户造成有害干扰的前提下为每个认知用户分配最佳的传输速率和发射功率，使认知用户与授权用户之间公平地共享信道资源。

1博弈论模型

在博弈论中，每个认知用户都是理性且自私的，他们都希望最大化自身的效用。把博弈论应用到功率控制中，并把认知用户的这种行为建模为一种非合作博弈模型，表示为

(1)

(2)

认知用户和授权用户共享频谱的功率控制问题就可以转化为对效用函数的设计和求解问题。

本文考虑在一个大型的3G异构蜂窝网络中(如图1所示)，存在一个未经授权的认知单蜂窝无线通信系统，认知系统中有N个认知用户(secondary user, SU)和认知基站BSS,认知用户以CDMA的通信方式与认知基站进行通信，另外授权系统中有一个授权用户(primary user, PU)和授权用户所在的基站BSP，系统中假设所有的认知用户都能正确地检测到空闲频谱。

图1　认知无线电模型场景Fig.1　Model scene for cognitive radio

认知用户为了和授权用户共享频谱资源，必须保证自身的传输功率不会对授权用户产生有害干扰，用户hi表示认知用户i与认知基站BSS的链路增益，gi表示认知用户i与授权用户所在基站BSP的链路增益，则认知用户i的信干比可以表示为[11]

(3)

(4)

2效用函数设计

文献[13]提出了基于非合作的联合速率和功率控制算法模型(non-cooperativejointpowerandratecontrolgame,NPRG)，效用函数的表达式为

(5)

(5)式中，K是可变参量，可以通过调整参数K保证认知用户所需信干比。该模型表示认知用户在较高信干比的情况下，通过对自身的传输速率和发射功率进行调整来最大化自身的效用。但是从(5)式可以看出，算法对认知用户没有任何的约束，但是在实际系统中，认知用户在和授权用户共享信道时，必须保证对其他认知用户的干扰和对授权用户的干扰在他们的可承受范围内，所以在NPRG算法中引入代价函数，该代价函数用来刻画对认知用户的惩罚，在带功率干扰代价的非合作联合功率速率控制博弈(non-cooperativejointpowerandratecontrolgamewithinterferencepowerpricing，NPRGP)算法中[11]采用了如下的效用函数

(6)

(6)式中，λ为常数。通过仿真对比分析，NPRGP算法中虽然认知用户能以更低的发射功率和传输速率传输数据，并且得到比较好的效用，但是因为代价函数中只考虑了认知用户的发射功率，而没有对认知用户的不同传输速率需求做出相应地应对措施，这样就有失公平性，针对此问题，基于公平性的原则[14]，本文用认知用户的实际传输速率和目标传输速率的差值平方与其他所有用户的差值平方之和的比值来定义惩罚因子，公式表示为

(7)

基于以上的考虑，本文提出的综合认知用户的发射功率和传输速率的效用函数表示为

(8)

3纳什均衡解的存在和唯一性

在发射功率和传输速率联合控制的模型中，不但在发射功率还要在传输速率上证明纳什均衡解的存在和唯一性。

根据超模博弈[15]的定义，如果满足以下条件，我们就称为超模博弈。根据超模博弈性质，如果本文所提算法满足超模博弈，那它就存在纳什均衡解，并且唯一存在。

1)所有参与者的策略空间是紧集合。

(9)

再将(9)式对pj取二阶导数得出

(10)

(10)式显然成立，即该模型在发射功率上存在并唯一存在纳什均衡解。

(11)

(12)

4仿真结果与分析

考虑在一个3G无线蜂窝网络中，授权用户所在的基站BSP的通信半径为3 000m，认知网路中认知基站BSS的通信半径为500m，有10个认知用户与授权用户共享带宽W=3.84×106Hz，认知用户均匀地分布在认知基站周围，它们到认知基站的距离矢量为：d=[50,100,150,200,250,300,350,400,450,500]m，对应各距离各认知用户的目标传输速率为r′tar=[96,85,75,65,55,45,40,35,30,25]kbit/s，认知用户的目标信干比设为rtar=12.42，可以算出K=0.218 86(K值的求法见文献[11])。

基于以上分析，本文采用Matlab仿真工具对本文所提算法的性能进行分析，与代价函数中只考虑认知用户的发射功率的NPRGP算法和认知用户的传输速率采用固定值、只单独对认知用户的发射功率进行控制的NPGP算法进行了对比，从多角度来证明本文算法的优越性。

这里简要对NPGP算法进行介绍，在NPGP算法中，每个认知用户采用相同的传输速率进行通信，具体的信干比和效用函数的表达式分别为

(13)

(14)

认知用户不管是通过何种手段调整自身的策略，其目的都是为了以最小的代价获得最大的效用。先对认知用户的收益进行仿真，结果如图2、图3所示。

图2　认知用户的效用函数随距离的变化Fig.2　Change of cognitive user’s utilityfunction with distance

图3　认知用户的发射功率随距离的变化Fig.3　Change of cognitive user’s transmit powerwith distance

从图2可以看出，在采用发射功率和传输速率联合控制的NPRGP算法和本文算法中，认知用户的效用函数明显高于NPGP算法。因为在对认知用户的发射功率进行控制的同时针对各认知用户的需求进行灵活的传输速率分配，可以达到整体上以更少的功率来传送更多比特数的目的。并且本文算法相比NPRGP算法和NPGP算法，效用函数的变化趋势较为缓慢，因为本文采用了基于公平性的惩罚因子，使得认知用户之间的差异变小，更体现了认知用户之间的公平性。

从图3中可以看出，在采用发射功率和传输速率联合控制的NPRGP算法和本文算法中，认知用户的发射功率明显低于NPGP算法，并且本文算法相对NPRGP算法，发射功率的变化趋势更为缓慢，认知用户不会为了自私地增大自身的效用而增大自身的发射功率，更体现了认知用户之间的“合作”，虽然存在部分认知用户的发射功率大于NPRGP算法中的发射功率，但是认知用户的效用几乎没有受到影响。

图4对认知用户的传输速率进行了对比分析，随着认知用户与基站的距离增加，认知用户的传输速率呈下降趋势，在NPGP算法中，每个认知用户采用相同的传输速率发送数据来保证其目标信干比，NPRGP算法和本文算法中，认知用户的传输速率的变化趋势是相似的，都是距离基站较近的用户的传输速率相对大些，但是由于NPRGP算法中没有考虑到功率分配的公平性，每个认知用户的传输速率差距比较大，本文采用传输速率的惩罚因子，让更接近目标传输速率的认知用户的惩罚相对小一点，否则惩罚就相对大一点，各认知用户之间的传输速率差异较小，体现了认知用户在传输速率分配上的公平性。

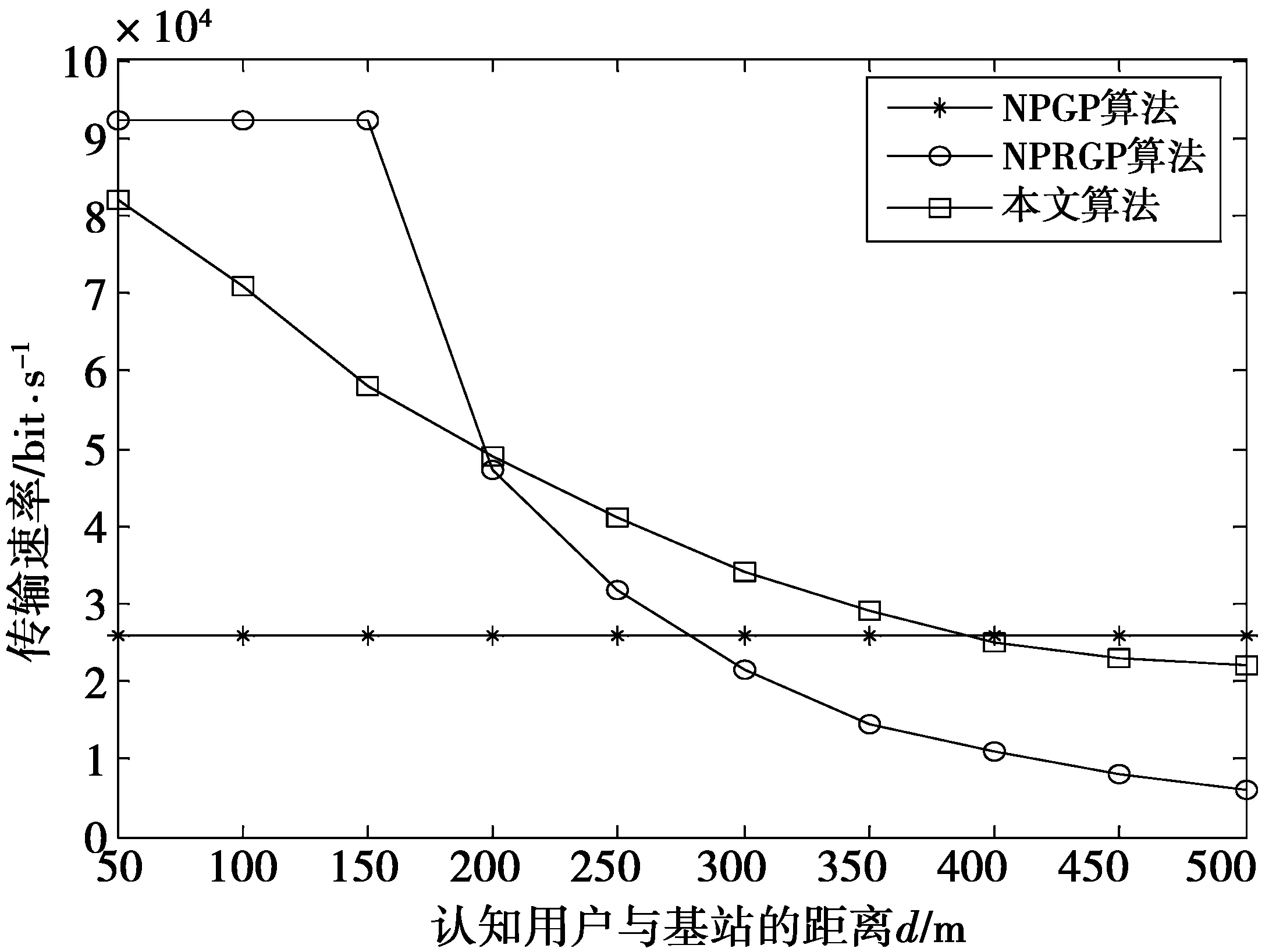
图4　认知用户的传输速率随距离的变化Fig.4　Change of cognitive user’s transmission ratewith distance

5结束语

本章考虑了多业务环境下，各个认知用户根据不同的业务需要不同的传输速率的问题，在对认知用户的发射功率进行控制的同时，对认知用户的传输速率进行了不同的分配，并且在现有的功率控制和传输速率联合控制的博弈模型中进行改进，提出基于公平性的惩罚因子，同时在代价函数中考虑了认知用户受到的干扰，让受到干扰大的用户惩罚相对小一点，兼顾了认知用户之间的公平性，并分别从理论上和用matlab工具仿真对所提算法的性能进行了分析和验证，结果表明，本文算法对认知用户的传输速率和发射功率进行联合控制，与传输速率固定的NPGP算法相比，认知用户能以较低的发射功率获得相对较大的效用，并且本文算法在传输速率分配上与各认知用户目标传输速率的距离更小，体现了本文算法在传输速率分配上的公平性。

参考文献：

[1]刘冰,万佑红.CDMA系统中基于博弈论的速率与功率联合控制[J].计算机技术与发展，2012，22(11)：53-56,60.

LIU Bing, WAN Youhong. Joint Control of Rate ad Power in CDMA System Based on Game Theory[J]. Computer Technology and Development,2012,22(11):53-56,60.

[2]徐德娜.集中式认知用户频谱分配策略及性能分析[D].河北秦皇岛:燕山大学,2012.

XU Dena. Centralized Spectrum Allocation Strategy for Cognitive Radio Users and Performance Analysis[D]. Qinhuangdao Hebei: Yanshan University, 2012.

[3]MARCUS M J. Real time spectrum markets and interruptible spectrum: New concepts of spectrum use enabled by cognitive radio[C]//New concepts of spectrum use enabled by cognitive radio. In Proc. of IEEE 1st Symposium on New Frontiers in Dynamic Spectrum Access Networks. Baltimore, MD, USA: IEEE Press, 2005: 512-517.

[4]杨路,朱嘉羲,马广浩. OFDM系统中基于二阶多项式奈奎斯特窗的边带加窗技术研究[J].重庆邮电大学学报：自然科学版，2014,26(3):325-329.

YANG Lu, ZHU Jiaxi, MA Guanghao. Edge windowing of second order polynomial Nyquist windows in OFDM systems[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2014,26(3):325-329.

[5]登伯格,梯诺尔.博弈论[M].北京：中国人民大学出版社,2002.

DENBERG N. Ladder game theory[M]. Beijing: Renmin University of China press,2002.

[6]余翔,张小银,刘磊. 基于归一化效用函数的功率控制算法研究[J].电信科学,2014,30(12):71-75.

YU Xiang, ZHANG Xiaoyin, LIU Lei. Power Control Algorithm Based on Normalized Utility Function Research[J]. Telecommunications Science,2014,30(12):71-75.

[7]MUSKU M R, CHRONOPOULOS A T, POPESCU D C. Joint rate and power control using game theory[C]//Proceedings of IEEE Consumer Communications and Networking Conferences.[s.l.]:IEEE Press,2006: 1258-1262.

[8]ZHOU P,LIU W,YUAN W,et al.Energy-efficient Joint Power and Rate Control via Pricing in Wireless Data Networks[C]//Proc.of Wireless Commiunications and Networking Conference.[s.l.]:IEEE Press,2008:1091-1096.

[9]冯雅楠.CDMA系统中基于多目标优化的功率控制机制的设计与仿真[D].沈阳:东北大学,2011.

FENG Yanan. Design and Simulation of Power Control Schemes Based on Multi-objective Optimization[D]. Shenyang: Northeastern University, 2011.

[10] BERRY J H, HONIG R A. Distributed interference compensation for wireless networks[J].Selected Areas in Communications,IEEE Journal on,2006,24(5):1074-1084.

[11] ZHOU P, YUAN W, LIU W, et al. Joint power and rate control in cognitive radio networks: a game-theoretical approach[C]//Communicatio ns, 2008. ICC'08. IEEE International Conference on .Beijing China: IEEE Press, 2008: 3296-3301.

[12] CHE Y,WANG J,CHEN J,et al.Hybrid power control scheme in hierarchical spectrum sharing network for cognitive radio[J].Physical Communication,2009(2):73-86.

[13] 杨晓花, 罗云峰, 吴辉球. Bertrand模型与超模博弈[J]. 中国管理科学, 2009, 17(1): 95-100.YANG Xiaohua, LUO Yunfeng,WU Huiqiu. Bertrand Model and the Theory of Supermodular Games[J].Chinese Journal of Management Science,2009,17(1):95-100.

[14] 王贻彬,倪卫明.认知无线电中基于博弈论方法的联合功率速率控制[J].计算机工程,2014,40(9):102-105.

WANG Yibin, NI Weiming. Joint Power and Rate Control Based on Game-theoretic Approach in Cognitive Radio[J]. Computer Engineering, 2014, 40(9):102-105.

[15] 王娇.认知无线电网络中功率控制优化算法的研究 [D] .北京：北京交通大学，2014.

WANG Jiao. Research on Power Control Optimization Algorithm in Cognitive Radio Networks[D]. Beijing: Beijing jiaotong University,2014.

Non-cooperative game of joint power and rate control algorithm

YU Xiang，ZHANG Xiaoyin

(School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065，P.R.China)

Abstract:The existing algorithm for the power control algorithm based on non-cooperative competition exists fairness problems between the second users, so this paper puts forward an algorithm in which the transmission power and the transmission rate are controlled at the same time. In the cost function a penalty factor based on transmission rate fairness is put forward, at the same time the second user’ interference is considered. Simulation comparison of the power control algorithm with fixed second user' transmission rate shows that the second user’ transmission rate and transmission power can make the distance between the transmission rate and the target transmission rate smaller, and can reflect the fairness among the second users.

Keywords：game theory; power control; rate control; fairness

DOI：10.3979/j.issn.1673-825X.2016.03.011

收稿日期：2015-04-20

修订日期：2016-04-06通讯作者：张小银zhangxxyy1112@163.com

基金项目：无线频谱监测接收机的数字化中频处理组件的研制；重庆市科技攻关项目(cstc2012gg-yyjs40006)

Foundation Items：Development of Digital Intermediate Frequency Processing Module for Wireless Spectrum Monitoring Receiver; The Key Science and Technology Research Project of CQ CSTC (cstc2012gg-yy40006)

中图分类号：TN914.53

文献标志码：A

文章编号：1673-825X(2016)03-0349-05

作者简介：

余翔，男，副教授，硕士生导师，主要研究方向为通信网络协议及安全等。E-mail: xiangyu@cqupt.edu.cn

张小银，女，硕士研究生，主要研究方向为宽带认知网络。E-mail:zhangxxyy1112@163.com

(编辑：张诚)