分级自适应伪贝叶斯时隙ALOHA控制算法
方 飞,余文春
(1. 内江师范学院 工程技术学院,四川 内江 641110;2.电子科技大学 通信学院,成都 611731)
分级自适应伪贝叶斯时隙ALOHA控制算法
方飞1,2,余文春1
(1. 内江师范学院 工程技术学院,四川 内江 641110;2.电子科技大学 通信学院,成都 611731)
摘要:时隙ALOHA需要使用控制算法以保证系统获得稳定吞吐量,而控制算法的关键是精确估计系统中的节点数。针对系统中的节点数在某时刻发生剧变时,传统的伪贝叶斯控制算法(pseudo Bayesian control algorithms,PBCA)存在调节时间较长的问题,提出分阶快速自适应伪贝叶斯控制算法(ranked fast adaptive PBCA,RFA-PBCA),首先设置一个门限值nth把信道的竞争情况分成高强度和低强度2种类型,再利用游程技术将信道分成空闲(冲突)和非空闲(非冲突)2种状态。当信道检测到c(c=6)个空闲时隙时,若估计节点数n大于nth,则节点将其传输数据概率增大为原先的2倍;同理,当信道检测c(c=6)个冲突时隙后,将其传输数据概率设为原先的1/2,其他情况下则采用PBCA进行调整。仿真结果表明,RFA-PBCA能够很好适应系统节点急剧变化的应用场景,其性能明显优于传统的PBCA。
关键词:时隙ALOHA;游程; 分阶快速自适应; 伪贝斯控制算法
0引言
时隙ALOHA及其改进协议[1]由于其简单性已经广泛应用于卫星通信,GSM数字蜂窝网络及标签识别[2]、认知无线网络[3-4]、车载网络[5]及水下传感网络等延时较长的环境下[6]。然而,时隙ALOHA本质上是不稳定的,文献[7]研究了有限用户时隙ALOHA系统的稳定范围。为解决时隙ALOHA的不稳定性,Rivest[8]提出的伪贝叶斯控制算法(pseudo Bayesian control algorithms,PBCA)依据信道的前一状态来修正系统的估计节点,更新节点的传输概率来实现系统的稳定性控制。文献[9]提出了在不同总体输入负载情况下采用不同的重传概率Pr的方式来获得系统的稳定性。Sarker研究了在控制新包生成率、允许某种程度的拒绝率及传输信道存在错误概率等多种环境下,有限次重传机制对系统稳定性的影响[10-12]。文献[13-16]依据系统的连续状态和节点间协作分析了系统性能,并将博弈理论引入到信道竞争中,并以此研究了时隙ALOHA系统的信道利用率和吞吐量。然而,这些稳定控制算法均是通过对系统中实际通信节点的准确估计,并调整各节点的数据发送概率从而实现系统稳定性的目的。
当系统节点数发生急剧变化时,信道将出现大量空闲或冲突时隙,造成信道利用率非常低。研究表明,当估计节点数与实际节点数之比大于2或小于0.5时,系统吞吐量低于最大理论吞吐量的50%。因此,若能采用某种控制算法将估计节点数同系统实际节点数之比调整到0.5—2,然后再采用精细调整算法,必能提高系统的整体吞吐量。本文基于通用的时隙ALOHA系统,借鉴Wang等在文献[17-18]中提出的检测固定大小的空闲时隙进行指数方式调节回退时间的原理,引入信道状态游程,采用“二分法”模型[19]得出信道状态的游程长度k的差分方程,并估计出信道状态的发生概率,从而估计出系统中的节点与估计节点数的差异。本文首先依据系统当前的估计节点数将信道竞争情况分成高负载和低负载2个等级,再依据信道状态的游程信息进行快速自适应调整,并将该算法与PBCA相结合,提出了分级快速自适应伪贝叶斯控制算法(ranked fast adaptive pseudo-bayesian control algorithm, RFA-PBCA)。最后利用MATLAB对该算法进行了仿真测试。
1伪贝叶斯控制算法
有限网络节点的系统,采用时隙ALOHA方式共享无线信道。时间轴被分成大小相同的时隙,时隙长度为发送一个数据帧所需的时间,每个节点只能在时隙开始时才允许发送数据。当2个及以上节点同时发送数据时,将产生冲突。发生冲突的节点在后续时隙重传产生冲突的数据包。因此,信道在任意时隙包含3种状态:空闲、成功及冲突,分别用{0,1,c}来表示。我们假定接收者在一个时隙成功接收一个数据包后,并在时隙结束时立即向所有用户反馈数据包传输结果。时隙ALOHA的基本原理如图1所示。
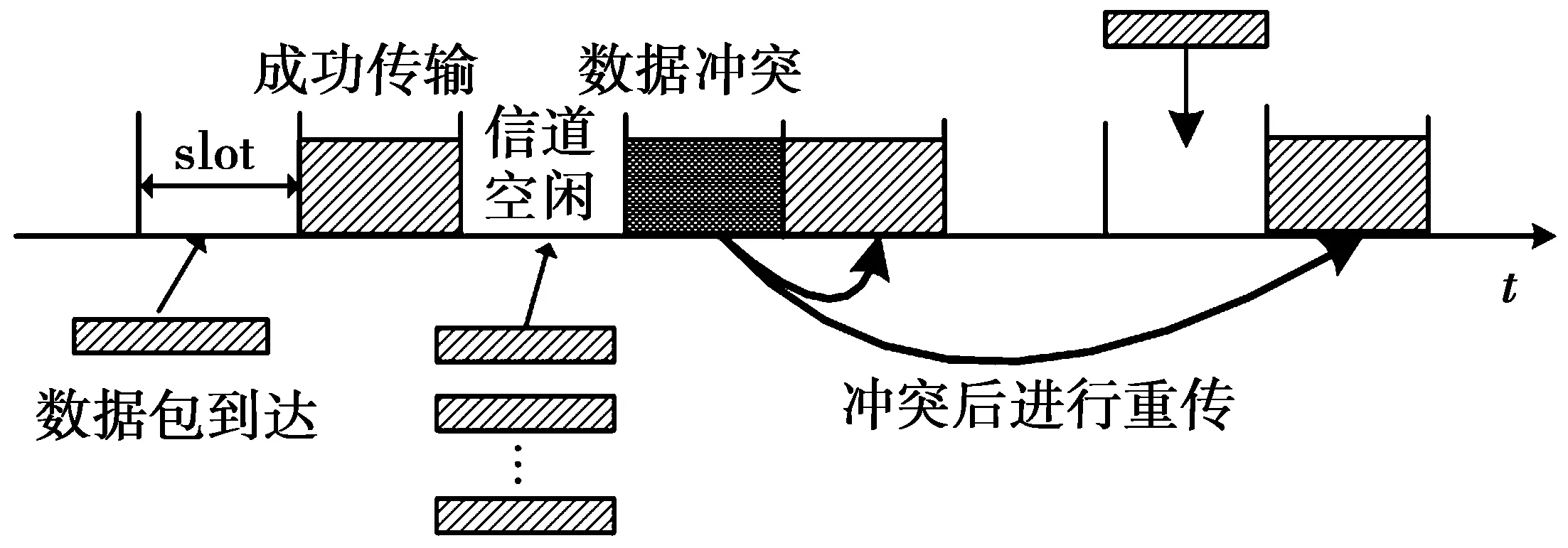
图1 时隙ALOHA系统原理图Fig.1 System principle diagram of slotted Aloha
采用时隙ALOHA作为MAC协议系统,有数据到达的节点是均值为m的泊松分布随机变量。假定在第i个时隙,信道有k个节点进行数据传输,其概率为
(1)
当每个网络节点以概率p=1/m进行发送时,则该时隙空闲的概率为
(2)
在第i个时隙空闲情况时,系统中还有k个终端等待发送的概率为
(3)
其概率是一个均值为m-1的泊松分布。
同理,当前有k个终端需要发送数据,成功传输的概率为
(4)
当在时隙i中成功传输一个网络节点的数据时,系统中有k+1个分组的概率为
P(mi=k+1|succ)=
(5)
可见系统中等待传输的分组数k是一个均值为m-1的泊松分布随机变量。考虑到系统在一个时隙内新到达的请求数为λ(≤0.368),给定一个与mi(mi≥1)相关的先验概率p=1/mi,当时隙空闲或成功后,mi+1是一个均值为mi+λ-1的泊松分布随机变量。若发生冲突,mi+1可近似为一个均值为mi+λ+1/(e-2)的泊松分布随机变量。因此,可根据当前时隙的状态进行下一时隙发送概率的调整,该算法称为伪贝叶斯算法(pseudo-bayesian control algorithm, PBCA),其算法实现步骤如下:
1)假定在时隙i,每个网络节点以概率P(mi)=min{1,1/mi}发送数据分组;
2)在i+1时隙的需要发送数据分组的终端数可以用(6)式进行估计。
(6)
3)下一时隙各终端以1/mi+1的概率发送请求分组。
在MATLAB平台下对PBCA进行仿真,假定系统在第30个时隙时刻系统处于稳定状态,在第30个时隙时刻节点数发生突变,PBCA调整过程中的系统吞吐量如图2所示。其中图2a为网络节点数(N=10,20,50)突变为200时PBCA的调整过程的系统吞吐量。图2b为系统节点数(N为50, 100, 200)突变为5时,PBCA调整过程中的系统吞吐量。图2中的吞吐量是指在500个时隙时间内,成功完成数据传输的时隙数所占的比例,是一个归一化值。从图2中可以看出,经过一段时间的调整,PBCA能够保证系统获得接近理论最大值的稳定吞吐量。但是,当节点数变化很大时,需要较长的时间才能获得理论最大值稳定吞吐量。

图2 PBCA调整过程中的平均吞吐量Fig.2 Throughput of PBCA in the adjusting
2S-ALOHA的信道状态游程分布
定义1N节点的S-ALOHA系统中,信道连续出现某种状态的长度称为信道的状态游程,连长为x个某种信道状态序列称信道状态游程为x。
使用二分法模型将信道状态分成空闲(或冲突)状态E和非空闲(非冲突)状态E′,并设E发生的概率为p。用t(t=1,2,…)表示时隙数,用s(t)表示在一个更新窗口内从t时隙开始的信道游程状态,假定各时隙信道状态独立,则s(t)为一维Markov链。依据游程的定义,游程k≥1,为了描述信道状态的转移过程,增加状态0,得到时隙ALOHA系统的信道状态E的游程状态转移如图3所示。

图3 时隙ALOHA信道状态E的游程Markov模型Fig.3 Markov model of run of channel state E of S-ALOHA
s(t)的状态转移概率为
(7)
2.1信道状态游程的差分方程
为研究S-ALOHA系统在不同节点和传输概率下信道状态的游程分布,先以样本取值元素个数为H(H≥2),各样本值依均匀分布(P=1/H)的随机试验X为参考模型,分析某一状态E(假定为X=1)的游程分布情况。
用k表示X=1游程的长度;用z(n)表示进行n次投币试验可能得到的互不重复的样本总个数;用x(n)表示样本中全部元素的个数;用G(n,k)表示连续进行n次试验形成的全部样本中游程恰好为k的游程总数。在MATLAB平台下编程实现n次投币试验的完备样本空间,并统计出不同n情况下G(n,k)的值。表1为H=2时,G(n,k)的统计值。令ξ=n-k,用G(ξ)表示所有样本空间中游程为k样本个数。
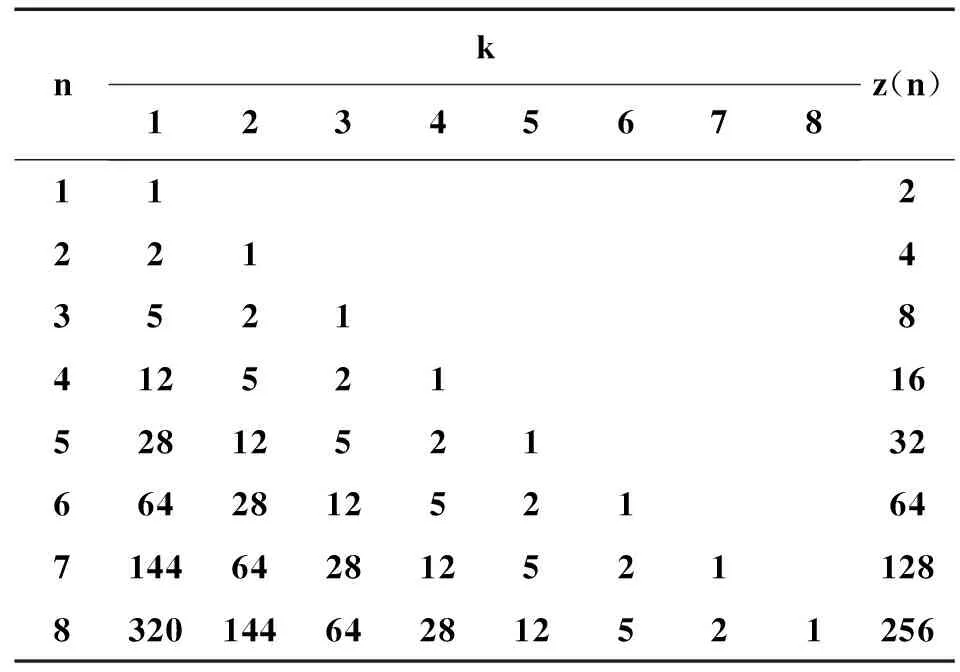
表1 H=2时,G(n,k)统计表
从表1可以看出,G(ξ)取值满足
1)当k=n(即ξ=0)时,G(0)=1;
2)当k=n-1(即ξ=1)时,G(1)=2(H-1);
3)当k≤n-2时,G(ξ)满足如下差分方程
(8)
另外,利用MATLAB程序获得H=3~9时G(n,k)的统计值,其结果仍然满足以上3点。求解(8)式的差分方程,并代入初始值G(1),G(2)得
(9)
用k替换变量ξ,用RL(k)表示n次试验中游程为k的可能出现次数,则
RL(k)=
(10)
将p=1/H代入(7)式,化简得
RL(k)=
(11)
在n次独立试验,每次试验可取值H种,样本总数z(n)=Hn=p-n,则平均每个样本中长度为k的游程个数为
g(k)=
(12)
另外,若将(6)式中的ξ用n-k进行替换,两端同除以Hn,则平均每个样本长度为k的游程个数g(k)(称g(k)为某状态的长度k游程的频次)的差分方程为
g(k)-2pg(k+1)+p2g(k+2)=0
(13)
求解(13)式并代入初始条件,即可得出(11)式。
采用组合方法获得的关于某事件状态游程的差分方程中,各事件个数为整数且依均匀分布出现,即事件元素取值H≥2,相应概率p=1/H≤0.5。但在时隙ALOHA系统中,信道状态虽然为空闲、成功传输及冲突3种情况,但其分布却不是等概率的。
采用“二分法”模型将概率空间划分为[0,p]和[p,1]2个部分,在MATLAB中运用蒙特卡洛方法模拟该随机试验,然后统计每个样本中游程为k的频次g′(k),并与(11)式得到的结论进行比较。模拟环境参数设置如下:样本容量n=100,样本个数(模拟次数)m=100 000。并将其与(12)式进行比较,其结果如图4所示。
图4的比较结果表明,当样本量很大时,模拟结果非常接近由(12)式得到的理论结果,表明g(k)与g′(k)满足同一个差分方程(13)式。由此可以得出,若某事件E发生的概率为p,其互斥事件E′发生的概率为1-p。在n次独立试验中平均每个样本中长度为k的游程个数满足差分方程(13)式。

图4 PBCA调整过程中的平均吞吐量Fig.4 Throughput of PBCA in the adjusting
2.2信道状态游程的概率分布
定义每个样本中状态E的长度为k的游程期望次数与该状态各种游程总的期望次数频次之比为长度为k某状态游程的概率密度函数f(k),即
(14)
而
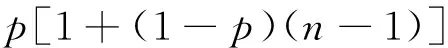
(15)
代入(14)式,得
f(k)=
(16)
当n→∞时,
(17)
(17)式表明当n较大时,信道某种状态的长度为k的游程分布可近似为几何分布随机变量。在n个时隙的数据传输所构形成的样本中,用变量R表示信道某种状态E的游程,长度不小于k的游程的概率分布为

(18)
当n→∞时,k≪n时,
(19)
定理1在时隙ALOHA系统中,将信道划分为空闲状态E(概率为p)和非空闲状态E′。在一个经过n(n>6)个时隙的传输后,若检测到信道空闲状态长度为6的游程序列,则在0.90的单侧置信区间认为p≥exp(-0.5)≈0.61,且系统的实际节点数小于估计节点数的1/2。
证明用变量R表示信道空闲状态E的游程,P[R (20) 由(17)式可知,要满足P[R F(k)=P[R≥k]<1-0.90=0.10 (21) 当n较大时,将p=exp(-0.5)≈0.61代入(19)式,(23)式的不等式变换为 -0.5(k-1)≤ln0.10 (k-1)≥-2ln0.05≈2*2.3≈5⟹k≥6 (22) 由(19)式易知,F(k)是p∈[0,1]单调递增函数,(22)式表明,当p 由(1)式,p=Pidle=exp(-N/M)≥exp(-0.5)时, N/M≤0.5⟹N≤M/2 (23) 定理1得证。 3分级自适应快速控制算法 3.1分级算法快速自适应算法设计 前一节定理表明,若系统连续检测到7个空闲状态(长度为7的信道空闲状态游程),在0.95的单侧置信区间认为信道空闲概率Pidle≥0.61,系统实际节点数小于当前窗口估计节点的0.5并将估计节点数M更新为原先的1/2(即M=M/2),同时节点使用新的概率P=1/M进行数据传输。同理,将信道状态分成冲突与非冲突2种状态,由(1)式,当系统的实际节点数N为估计节点数的2倍时,信道冲突的概率Pcoll≈0.6。且β=N/M越大,Pcoll越大。当系统检测长度为6的冲突状态游程时,在单侧0.90的置信区间亦可认为实际节点数N大于估计节点数M的2倍,控制算法即可调节节点的发送概率为原先的1/2。 然而,由PBCA算法中的(6)式可知,当系统检测到成功传输或信道空闲时,其调整步长为λ-1,而信道冲突后的调整步长为λ+1/(e-2)。λ作为新包生成率,应该满足λ≤0.368,在PBCA算法设计中,λ取系统最大理论吞吐量值0.368。假定系统估计节点数M小等于15时,系统实际节点数N小于M/3,各节点依据概率Pt=1/M进行数据传输,信道空闲的概率为 0.72 (24) 假定系统检测6个空闲时隙,并依据定理1将系统估计节点数调整为原先的一半。但实际上,由于每检测到一次空闲后,系统的估计节点会减小0.632。经过6次空闲后,系统估计节点已经变为10左右,若再进行减半调整,估计节点数变为5,与系统实际节点数相近。若再采用乘性控制算法,则容易产生振荡调整的过程,从而使信道吞吐量下降。针对该问题,提出的分级快速自适应控制算法做如下处理:依据估计节点数设置一个临界值Nth,当估计N 分级快速自适应伪贝叶斯控制(RFA-PBCA) 算法实现步骤如下: 1) 在时隙v,假定系统中的节点数为Nv,每个节点以概率qr(Nv)=min{1,1/Nv}发送数据分组; 2)快速自适应算法处理:若系统检测到游程为6的空闲状态时,且Nv>Nth将Nv+1=Nv/2;若系统检测到游程为6的冲突状态时,将Nv+1=2Nv;跳转到4); 3)正常的伪贝叶斯算法处理:下一时隙的需发送数据组的节点数用(25)式进行估计 (25) (25)式中,λ为新包到达率。由于时隙ALOHA的最大吞吐量为0.368,因此,在以后的仿真分析中,λ取0.368 4)下一时隙各节点以1/Nv+1的概率发送请求分组。 3.2算法仿真与验证 系统吞吐量是评价网络性能的重要指标,在基于竞争的MAC协议中,高的吞吐量也意味着低的时延。利用MATLAB工具对RFA-PBCA在稳定性调节过程的吞吐量及调节时间进行了仿真。仿真环境设置为:系统以时隙为单位进行划分,在起始时刻t0=0系统处于稳定状态,而在t=20节点数由m变化为n,仿真时间为200个时隙。 图5及图6是FA-PBCA与PBCA算法吞吐量性能比较图。其中,图5为系统初始节点数为较大值(m为80,200)剧变为较小值(2,5,10)环境下,系统调节过程中每个时间的平均吞吐量。图5a、图5b的仿真显示,当初始节点数越大,而变化后节点数越小,PBCA吞吐量越小,达到稳定最大吞吐量所需的时间越长。而RFA-PBCA能快速将系统吞吐量调节到稳定最大吞吐量。当系统节点数从较大的值变为很小的值时(如从200个节点突然变化为小于10个节点情况),在PBCA控制算法下经过近200个时隙的调整,系统的吞吐量也只能达到最大理论吞吐量的30%以下;而RFA-PBCA经过约30个时隙的调整就能达到最大吞吐的90%左右。 图5 m较大情况下RFA-PBCA与PBCA调节过程吞吐量Fig.5 Throughput of RFA-PBCA vs. PBCA as m is larger 图6 m较小情况下RFA-PBCA与PBCA吞吐量Fig.6 Throughput of RFA-PBCA vs. PBCA as m is smaller 图6为初始节点数较小(m为2,10)剧变为较大值(60,120,240)时系统RFA-PBCA与PBCA算法调节性能比较图,从仿真结果可以看出RFA-PBCA能明显提高系统的调节性能,加快调节速度。比较图5与图6可以看出,网络节点数从较大情况变为较小情况的调节时间大于网络节点从较小值变为较大值的场景。 为测试RFA-PBCA、PBCA的在不同节点变化情况下系统平均吞吐量性能,基于MATLAB仿真平台进行了仿真测试,仿真时间为200个时隙。得到各种场景下系统的平均吞吐量如图7所示。图7a、图7b为系统初始节点数较小情况下(m分别为2,10)在某一时隙节点数发生变化后,经过200个时隙得出的平均吞吐量。仿真结果表明,RFA-PBCA即使要系统节点增加到其15倍以上,也可以保证信道获得0.32的利用率,接近最大吞吐量的90%。图7c、图7d为系统初始节点数较大情况下(m分别为200、300)在某一时隙节点数发生变化后,经过200个时隙得出的平均吞吐量。从图7可以看出,即使节点数变为很小的值,RFA-PBCA可以在200时隙内的平均吞吐量大于0.32,大于时隙ALOHA系统的最大吞吐量0.368的90%,而采用传统的PBCA时,当系统节点数从比较大的值(大等于200)突变为一个很小的值时(如小于15),经过200个时隙后,得到的平均吞吐量仍低于0.1。 4结束语 当时隙ALOHA系统中的节点数在某时刻发生剧变时,传统的PBCA需要较长的时间才能达到稳定的接近最大理论值的吞吐量。分级快速自适应控制算法(FA)将信道状态分成空闲状态和非空闲状态,并依据系统当前的估计值设置了一个门限值nth(本算法中nth=15)。当信道检测到6个空闲时隙时,在0.90置信区间认为实际节点数为估计节点数的1/2,若当前估计节点m>nth,则将估计节点数M调整为M/2,若当前估计节点m 图7 RFA-PBCA与PBCA平均吞吐量Fig.7 Average Throughput of RFA-PBCA vs. PBCA 参考文献: [1]MA R T B, MISRA V, RUBENSTEIN D. An Analysis of Generalized Slotted-Aloha Protocols[J]. IEEE/ACM Transactions on Networking, 2009, 17(3): 936-949. [2]WU Haifeng, ZENG Yu, FENG Jihua, et al. Binary tree slotted ALOHA for passive RFID tag anticollision[J]. IEEE Transactions on Parallel and Distributed Systems, 2013, 24(1): 19-31. [3]YUN Hanbae.Analysis of Optimal Random Access for Broadcasting with Deadline in Cognitive Radio Networks[J].IEEE Communications Letters.2013,17(3):573-575. [4]WU Juanmei, WANG Yichen, DENG Jianguo. Performance of a Cognitive p-persistent Slotted Aloha Protocol[C]//Proc. 2015 IEEE International Conference on Communication Workshop. UK, London:IEEE press,2015: 405-410. [5]CHENG Nan, ZHANG Ning, LU Ning, et al. Opportunistic Spectrum Access for CR-VANETs: A Game Theoretic Approach[J]. IEEE Transactions on Vehicular Technology, 2013, 63(1): 237-251. [6]PU Lina, LUO Yu, ZHU Yibo, et al. Impact of real modem characteristics on practical underwater MAC design[C]// Proc. 2012 OCEANS. korea ,Yeosu:IEEE press,2012:1-6. [7]HUI Hungka,YUE Onching,WING Cheong lau.FRASA:Feedback Retransmission Approximation for the Stability Region of Finite-User Slotted ALOHA[J].IEEE Transactions on Information Theory,2013,59(1):384-396. [8]RIVEST R L. Network Control by Bayesian Broadcast[J]. IEEE Transactions on Information Theory, 1987, 33(3): 323-328. [9]LOREN P C. Control procedures for slotted Aloha systems that achieve stability [J]. ACM SIGCOMM Computer Communication Review, 1986, 16(3): 302-309. [10] SARKER J H. Auto-controlled algorithm for slotted ALOHA[J]. IEE Proceedings Communications, 2003, 150(1): 53-58. [11] SARKER J H, MOUFTAH H T. A Retransmission Cut-Off Random Access Protocol with Multi-packet Reception Capability for Wireless Networks[C]//Proc. 3rd International Conference on Sensor Technologies and Applications. Athens,Greece: IEEE press.2009:217-222. [12] SARKER J H. Stable and unstable operating regions of slotted ALOHA with number of retransmission attempts and number of power levels[J]. IEE Proceedings Communications, 2006, 153(3): 355-364. [13] YOUNGMI J, KESIDIS G, JU W J. A Channel Aware MAC Protocol in an ALOHA Network with Selfish Users[J]. IEEE Journal on Selected Areas in Communications,2012, 30(1): 128-137. [14] BARCELO J, INALTEKIN H, BELLALTA B. Obey or Play: Asymptotic Equivalence of Slotted Aloha with a Game Theoretic Contention Model[J]. Communications Letters, IEEE, 2011, 15(6): 623-625. [15] JEON W S, JEONG D G. Combined Channel Access and Sensing in Cognitive Radio Slotted-ALOHA Networks[J]. IEEE Transactions on Vehicular Technology, 2015, 64(5): 2128-2133. [16] LYU J, CHEW Y H, WONG W C. Aloha Games with Spatial Reuse[J]. IEEE Transactions on Wireless Communications, 2013, 12(8): 3932-3941. [17] WANG Chonggang, LI Bo, LI lemin. A new collision resolution mechanism to enhance the performance of IEEE 802.11 dcf[J].IEEE Transactions On Vehicular Technology, 2004, 53(4):1235-1246. [18] WU Huasen, ZHU Chenxi, LA R J. FASA: Accelerated S-ALOHA Using Access History for Event-Driven M2M Communications[J]. IEEE/ACM Transactions on Networking, 2013, 99(2): 1-14. [19] 马秀峰.随机序列轮长与轮次的统计规则[J].水科学进展,1994, 5(2):95-100. MA Xiufeng. Run and Run-Length Characteristics of Stochastic Sequences[J]. Advance in Water Science, 1994, 5(2):95-100. [20] FANG Fei, MAO Yuming, LENG Supeng. An adaptive Slotted ALOHA Algorithm[J]. Przeglad elektrotechniczny(Electrical Review), 2012, 88(5b): 17-21. Ranked adaptive pseudo bayesian control algorithm for slotted ALOHA FANG Fei1,2,YU Wenchun1 (1. Engineering and Technology College of NeiJiang Normal University, NeiJiang 641110, P. R. China;2. School of Communication and Information Engineering, University of Electronic Science and Technology of China,Chengdu 611731, P. R. China) Abstract:The control algorithm is necessary for slotted ALOHA in order to achieve the stable system throughput. The essentiality of control algorithm is to derive the acute number of system nodes. The classic control algorithm suffers performance loss when the system nodes sharply changes. In this paper, a ranked fast adaptive pseudo Bayesian control algorithm (RFA-PBCA) was proposed to promote the performance of ALOHA. Firstly, a threshold valuenthis set up to divide the channel into two types of high intensity and low intensity. Then, the channels are grouped into two states, idle (or conflict) and not idle(or not conflict) by the technology of run. When 6 idle channels are detected and the number of estimated nodenis greater thannth, all nodes update their probability of transmitting data as 2 times. Similarly, if 6 collision slots are detected, the number of estimate nodes will be doubled and the probability of transmitting data is updated as 1/2 times. In other cases, the pseudo Bayesian control algorithms (PBCA) are adopted. The results of simulation show that can PFA-PBCA well adapt to the scenarios where node of system rapidly changes, its performance outperforms than pseudo-Bayesian control algorithms. Keywords:slotted ALOHA; run; ranked fast adaptive; pseudo-bayesian control algorithm DOI:10.3979/j.issn.1673-825X.2016.03.004 收稿日期:2015-12-22 修订日期:2016-06-12通讯作者:方飞fangfei_nj@163.com 基金项目:国家自然科学基金(61471102);四川省教育厅重点项目资助(13ZA0005) Foundation Items:The National Natural Science Foundation of China(61471102);The Key Project of Sichuan Education Department(13ZA0005.) 中图分类号:TN929.5 文献标志码:A 文章编号:1673-825X(2016)03-0303-09 作者简介: 方飞(1974-),男,四川南江人,副教授,博士。主要研究方向为宽带无线局域网络、物联网。E-mail:fangfei_nj@163.com。 余文春(1974-),男,四川广元人,讲师,硕士。主要研究方向为网络数据库,物联网。E-mail: ywclmxx@163.com。 (编辑:张诚)