巧用向量结论妙解最值问题
2016-07-04 05:52江西
高中数理化 2016年12期
◇ 江西 曾 敏
巧用向量结论妙解最值问题
◇江西曾敏
平面向量数量积是高考的重、难点.教学中笔者发现结合平面向量数量积的一个关系式,再利用向量加、减法的三角形法则,可得到如下结论.

图1
结论在△ABC中,M为BC的中点,则





利用上面的结论解决向量最值问题时,往往会收到事半功倍的效果.


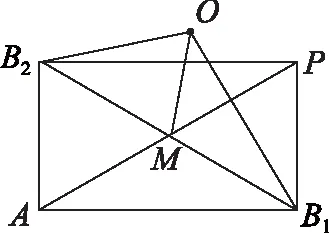
图2
依题意,可构造矩形AB1PB2(如图2),连接AP与B1B2交于点M.利用平面向量结论易知:在△OAP中,
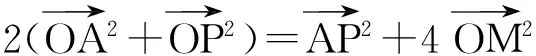
在△OB1B2中,

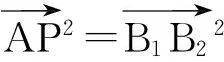
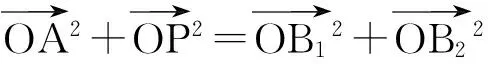

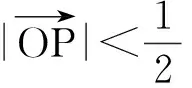
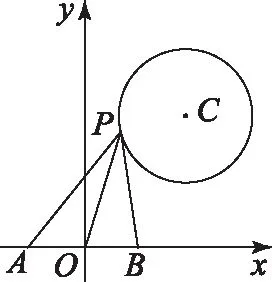
图3


2(|PA|2+|PB|2)=|AB|2+4|PO|2,

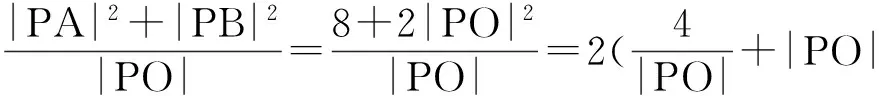
因为|OC|-r≤|PO|≤|OC|+r,所以|PO|∈[3,7].所以当 |PO|=3时,

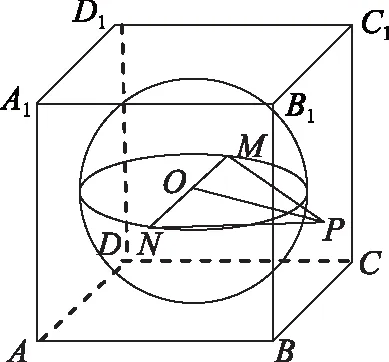
图4


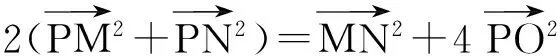

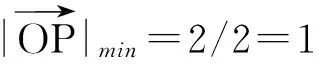

当P在正方体顶点时,



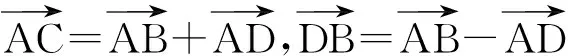
向量中的最值与范围问题是向量的一大亮点,解决好此类问题,不仅可以提高学生分析问题和解决问题的能力,而且可以提高数学应用能力和综合能力.
(作者单位:江西师大附中)
猜你喜欢
现代苏州(2022年14期)2022-08-05
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
数学小灵通(1-2年级)(2020年11期)2020-12-28
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
小学生优秀作文(低年级)(2018年11期)2018-11-14
中学生数理化·高一版(2016年4期)2016-11-19
公民与法治(2016年10期)2016-05-17
老友(2011年3期)2011-06-09

