基于多元回归分析的泥水盾构施工参数分析

廖利钊 　陶　冶　刘　辉

(1.上海天佑工程咨询有限公司，上海　200092；2.华中科技大学　土木学院工程管理研究所，武汉　430074)

基于多元回归分析的泥水盾构施工参数分析

廖利钊1陶冶2刘辉2

(1.上海天佑工程咨询有限公司，上海200092；2.华中科技大学土木学院工程管理研究所，武汉430074)

【摘要】盾构法施工技术在地铁工程建设中逐步得到广泛应用，对于盾构施工多参数的相关性分析研究更是少之又少，在这之中大多又是将土压平衡盾构作为研究对象，泥水盾构施工参数的多元线性回归分析几乎成了相关研究领域的空白。所以，有必要对泥水盾构施工参数的多元线性回归分析进行研究，从而保证施工过程的安全，降低工程造价，减少地铁施工的不利影响。本文以武汉轨道交通4号线左线757环到1460环的现场盾构施工数据，利用SPSS统计学软件对数据进行统计分析，建立起总推力和扭矩的多元线性回归模型，通过求解出的多元线性回归模型，对盾构施工工程中的总推力和扭矩进行预测。用右线的现场盾构施工数据进行工程验证，发现预测结果与实际结果吻合较好。

【关键词】泥水盾构；盾构参数；统计分析；线性回归；预测

【DOI】 10.16670/j.cnki.cn11-5823/tu.2016.03.18

引言

改革开放以来，伴随着城市化进程的加快，城市规模不断扩大，城市人口集聚膨胀。需求多城市出现了用地紧张、交通拥堵、环境污染严重、能源消耗加剧等问题，这给城市生活带来了巨大的影响。如表1所示，2014年末，全国共有22个城市建成轨道交通，线路长度2 715km，比上年增22.7%；全国36个城市在建轨道交通，线路长3 004km，比上年增长8.8%[1]。由此看来，地铁的建设需求非常旺盛，发展十分迅速。

表12010—2014年城市轨道交通统计

年份建成轨道交通的城市个数(个)建成轨道交通线路长度(km)正在建设轨道交通的城市个数(个)正在建设轨道交通线路长度(km)20101214292817412011121672281891201216200629206020131622133527602014222715363004

盾构法施工是城市地下工程建设的主要手段之一。由于作业面在地面以下，避免了开槽明挖的一些缺点，对周围环境影响较小，施工中不会引起水位降低，开挖引起地表沉降较小，掘进速度较快，隧洞成型质量较好，施工环境较好，机械化程度高，具有人性化，噪音小，占用场地少，施工中支护衬砌质量可靠且造价较低，施工穿越河道不受影响，受天气影响较小在土质差水位高的条件下建设埋深较大的隧道时有较高的技术经济优越性[2]。

掘进参数间存在不同程度的相关性，同时，各参数还受到诸多外界因素(地质条件、人为操作水平、系统运行状态等)的影响和控制，所以，盾构掘进参数是盾构掘进系统稳定性和效率性的直接体现。因此，盾构掘进参数控制是盾构施工中的重要环节，如何合理的选择盾构掘进参数成为了一个非常值得研究的课题。这对于现场施工及以后的研究意义重大。

1盾构参数的相关研究

1.1目前国内外学者对于盾构施工参数之间关系的研究现状

蒋洪进[3]结合上海市西藏南路越江隧道工程实践，对该工程西线、东线二台Ф11.58m 大直径泥水盾构近距离(最小净距3.30m)穿越既有地铁 M8 线隧道上、下行线期间，电子水平尺采集的沉降数据进行了分析，研究了泥水盾构施工参数变化对沉降产生的影响和施工参数，以及控制后期沉降的措施。

朱宏伟[4]在泥水盾构掘进速度的影响因素及数值分析中，介绍了如何设定泥水加压盾构的施工参数，并结合地铁施工数据，分析各施工参数对掘进速度的影响程度，同时利用多元统计方法求解出了泥水加压盾构掘进速度的数学表达式。Bruines[5]于2001年强调TBM与岩体间是一个动态的、不确定的、非线性的相互作用过程，应用模糊神经网络方法，采用5个参数预测了 TBM的施工进度。

1.2本文研究思路及手段

本文以武汉轨道交通4号线左线757环到1 460环的现场盾构施工数据，利用SPSS统计学软件对数据进行统计分析。

首先选取合适的盾构掘进参数，并进行相关性分析和标准化处理，然后利用SPSS的回归分析功能建立起总推力和扭矩的多元线性回归模型，通过求解出的多元线性回归模型，用来预测施工的总推力和扭矩。用右线的现场盾构施工数据进行工程验证，发现预测结果与实际结果吻合较好。

2盾构参数的选取和处理

2.1工程概况

武汉市轨道交通四号线二期工程起点位于汉阳永安堂，线路沿汉阳大道向东至钟家村，右转走鹦鹉大道，自拦江路口下穿，沿腰路堤路走行，穿越长江后沿紫阳路走行，至首义路。线路全长约15.6km，起点～龙阳大道为地面高架，其余为地下工程。工程地理位置见图1武汉市轨道交通四号线地理位置图。

2.2盾构参数的选取

盾构法施工涉及的掘进参数众多，多达数十个，并且各个参数受到地质条件、人为操作水平、系统运行状态等多重因素的影响，所以，掘进参数的选取应能体现影响因素的作用。本文基于以上考虑，从众多掘进参数中选取了8个有效参数用于分析讨论，分别是平均转速、平均扭矩、总推力、推进速度、贯入度、灌浆量、气仓压力和泥水仓压力。其中，转速主要受人为操作水平的影响，灌浆量、气仓压力、泥水仓压力是系统运行状态的体现，扭矩、总推力、推进速度、贯入度受地质条件的影响较大。综上考虑，本文觉得选取这8个参数来进行分析是合理的。

2.3盾构参数的标准化处理

在数据分析之前，我们需要先将数据标准化，利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题，对不同性质指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对测评方案的作用力同趋化，再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。数据标准化的方法有很多种，本文将采用“Z-score标准化”的方法将盾构参数进行标准化处理。

2.4盾构参数规律分析

利用标准化后的数据，通过研究盾构参数的两两相关性，可以求出两两参数间的相关系数，利用统计学方法算得各掘进参数相关系数矩阵如表2。

从各掘进参数相关系数矩阵中可以看出：

(1)与总推力显著相关的盾构参数有：平均转速、平均扭矩、推进速度、总灌浆量、贯入度、泥水仓压力；

(2)与平均扭矩显著相关的盾构参数有：平均转速、推进速度、总推力、气仓压力、泥水仓压力。

3盾构掘进效率与掘进参数的分析研究

3.1总推力的多元线性回归分析建模

由2.4的盾构参数规律性分析确定了与总推力显著相关的6个盾构参数，分别是：平均转速、平均扭矩、推进速度、总灌浆量、贯入度、泥水仓压力。并将这6个盾构参数作为变量对总推力进行回归。

为了研究平均转速、平均扭矩、推进速度、总灌浆量、贯入度、泥水仓压力和总推力间的数学关系，对702组现场盾构数据进行线性回归分析。

选择多元线性回归模型如下式：

F=α+β1X转+β2X扭+β3X速+β4X灌+β5X贯+β6X泥

(3-1)

式中，F表示总推力(kN)，X转、X扭、X速、X灌、X贯、X泥分别表示平均转速(RPM)、平均扭矩(MNm)、推进速度(mm/min)、总灌浆量、贯入度(mm/rev)、泥水仓压力(bar)，α、β1、β2、β3、β4、β5、β6均为回归系数。

利用spss统计学软件，首先对该多元回归模型的显著性进行F检验，得到如表2。从表1中可以看出，F检验的p值(表中的Sig.列数值)小于0.05，说明方程通过了显著性检验，说明选定盾构参数与总推力的多元线性回归达到显著水平。

对标准化后的数据进行多元回归分析，并得到回归系数表3，表中非标准化系数的B列列出了α、β1、β2、β3、β4、β5、β6求解出的具体数值。因此总推力的多元线性表达式为：

F=-2.89×10-15+0.275X转+0.526X扭-0.315X速-0.18 X灌-0.104X贯+0.037X泥

(3-2)

3.2总推力的多元线性回归模型的精度分析

由于盾构参数和总推力之间存在相关性并不代表该施工参数对掘进速度的影响一定显著，所以还需结合t检验进行分析对上述表达式进行精度分析。t检验是针对数学关系式中某项变量的系数是否可能为0的假设的检验。t值的绝对值越大，概率越小(该项概率即为该项变量的系数为0的概率)，影响越显著。t值检验的结果即为表3的最后两列。

从表格中可以看出，仅平均扭矩和总灌浆量t检验的p值小于0.05，说明仅平均扭矩和总灌浆量对总推力的偏回归系数达到极显著水平。平均转速和推进速度的t检验p值达到了0.1，认为在可接受范围内，也将其作为显著变量。剔除不显著变量，仅以平均扭矩和总灌浆量为变量，重新对总推力的多元线性回归模型进行回归分析。

首先依然要对调整后的多元线性回归模型进行显著性分析，F检验结果如表4。从表4可以看出，F检验的p值小于0.05，故调整后的多元线性回归模型通过了显著性检验。

同样对标准化后的数据进行多元线性回归分析，得到回归系数如表5：从表5中可以看出，平均转速、平均扭矩、推进速度和总灌浆量均达到显著水平。因此，调整后的多元线性回归表达式为：

F=0.415X转+0.528X扭-0.504X推-0.178 X灌

(3-3)

表1各掘进参数相关系数矩阵

平均转速平均扭矩推进速度总推力总灌浆量贯入度气仓压力泥水仓压力平均转速Pearson相关性1-0.870**0.802**-0.437**-0.0670.145**0.0570.011显著性(双侧)0000.07600.1280.778N702702702702702702702702平均扭矩Pearson相关性-0.870**1-0.646**0.483**0.054-0.061-0.132**-0.078*显著性(双侧)0000.150.10600.04N702702702702702702702702推进速度Pearson相关性0.802**-0.646**1-0.486**-0.153**0.686**-0.163**-0.216**显著性(双侧)0000000N702702702702702702702702总推力Pearson相关性-0.437**0.483**-0.486**1-0.100**-0.293**0.0180.085*显著性(双侧)0000.00800.6290.025N702702702702702702702702总灌浆量Pearson相关性-0.0670.054-0.153**-0.100**1-0.171**0.0440.091*显著性(双侧)0.0760.1500.00800.2430.015N702702702702702702702702贯入度Pearson相关性0.145**-0.0610.686**-0.293**-0.171**1-0.301**-0.325**显著性(双侧)00.10600000N702702702702702702702702气仓压力Pearson相关性0.057-0.132**-0.163**0.0180.044-0.301**10.943**显著性(双侧)0.128000.6290.24300N702702702702702702702702泥水仓压力Pearson相关性0.011-0.078*-0.216**0.085*0.091*-0.325**0.943**1显著性(双侧)0.7780.0400.0250.01500N702702702702702702702702 **.在0.01水平(双侧)上显著相关。 *.在0.05水平(双侧)上显著相关。 Zscore表示经过“Zscore标准化”以后的参数

表2方差分析b

模型平方和df均方FSig.1回归237.016639.50359.1710.000a残差463.9846950.668总计701.000701

表3回归系数a

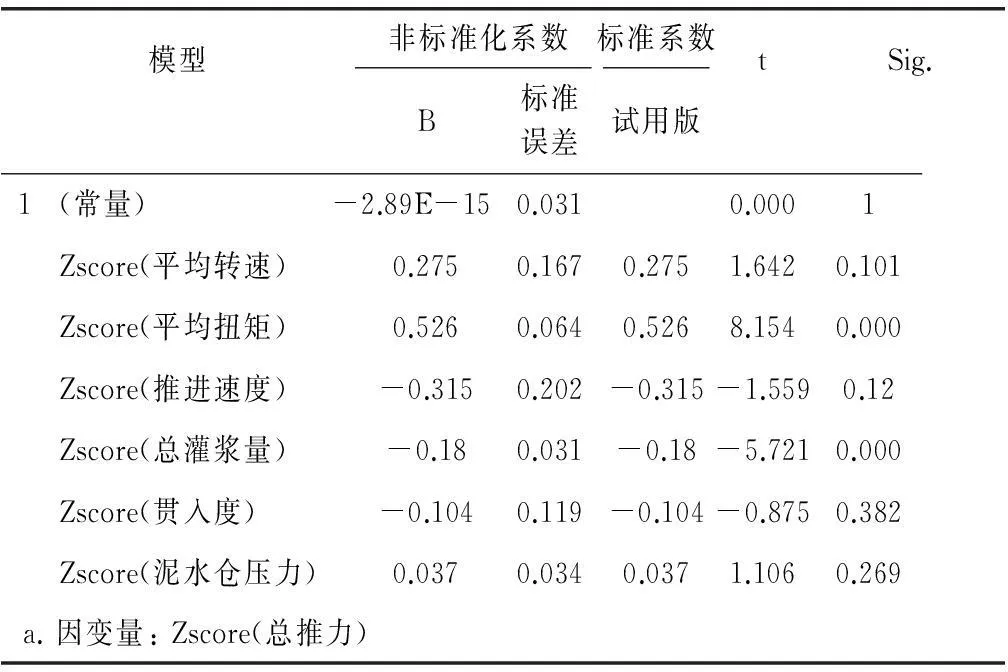
模型非标准化系数标准系数tSig.B标准误差试用版1(常量)-2.89E-15 0.0310.0001Zscore(平均转速)0.2750.1670.2751.6420.101Zscore(平均扭矩)0.5260.0640.5268.1540.000Zscore(推进速度)-0.3150.202-0.315-1.5590.12Zscore(总灌浆量)-0.180.031-0.18-5.7210.000Zscore(贯入度)-0.1040.119-0.104-0.8750.382Zscore(泥水仓压力)0.0370.0340.0371.1060.269a.因变量:Zscore(总推力)

表4方差分析b

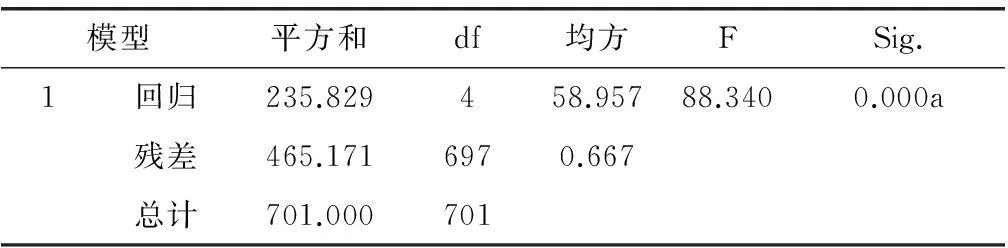
模型平方和df均方FSig.1回归235.829458.95788.3400.000a残差465.1716970.667总计701.000701

表5回归系数a

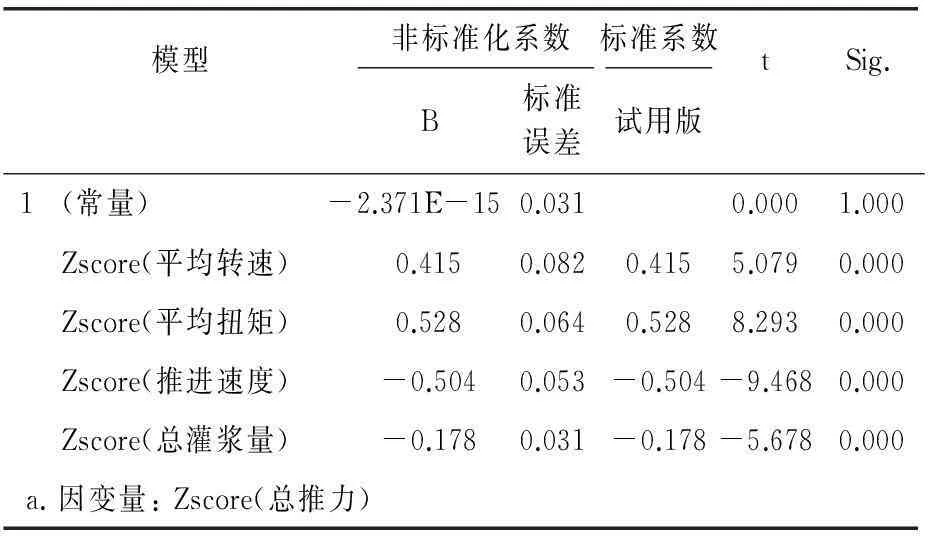
模型非标准化系数标准系数tSig.B标准误差试用版1(常量)-2.371E-15 0.0310.0001.000Zscore(平均转速)0.4150.0820.4155.0790.000Zscore(平均扭矩)0.5280.0640.5288.2930.000Zscore(推进速度)-0.5040.053-0.504-9.4680.000Zscore(总灌浆量)-0.1780.031-0.178-5.6780.000a.因变量:Zscore(总推力)

3.3扭矩的多元线性回归分析建模

由2.4的盾构参数规律性分析确定了与以此就确定了与扭矩显著相关的5个盾构参数，分别是：平均转速、推进速度、总推力、气仓压力、泥水仓压力。并将这5个盾构参数作为变量对总推力进行回归分析。

为了研究平均转速、推进速度、总推力、气仓压力、泥水仓压力和扭矩间的数学关系，对702组现场盾构数据进行线性回归分析。

选择多元线性回归模型为：

N=α+β1X转+β2X速+β3X推+β4X气+β5X泥

(3-4)

式中，N表示总推力(MNm)，X转、X扭、X速、X灌、X贯、X泥分别表示平均转速(RPM)、推进速度(mm/min)、总推力(kN)、气仓压力(bar)、泥水仓压力(bar)，α、β1、β2、β3、β4、β5均为回归系数。

利用spss统计学软件，首先对该多元回归模型的显著性进行F检验，得到如表6。

从表中可以看出，F检验的p值(表中的Sig.列数值)小于0.05，说明方程通过了显著性检验，说明选定盾构参数与扭矩的多元线性回归达到显著水平。

对标准化后的数据进行多元回归分析，并得到回归系数表7。

表6方差分析b

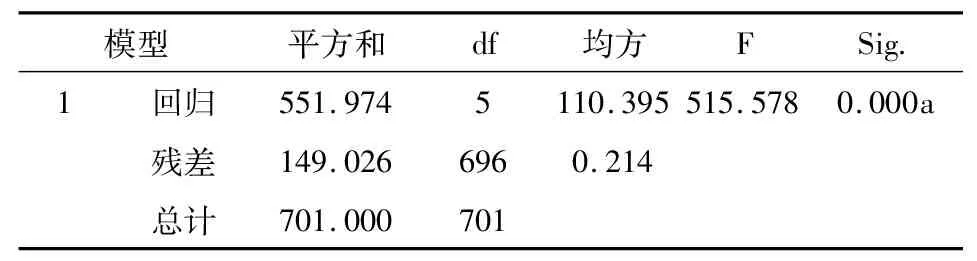
模型平方和df均方FSig.1回归551.9745110.395515.5780.000a残差149.0266960.214总计701.000701

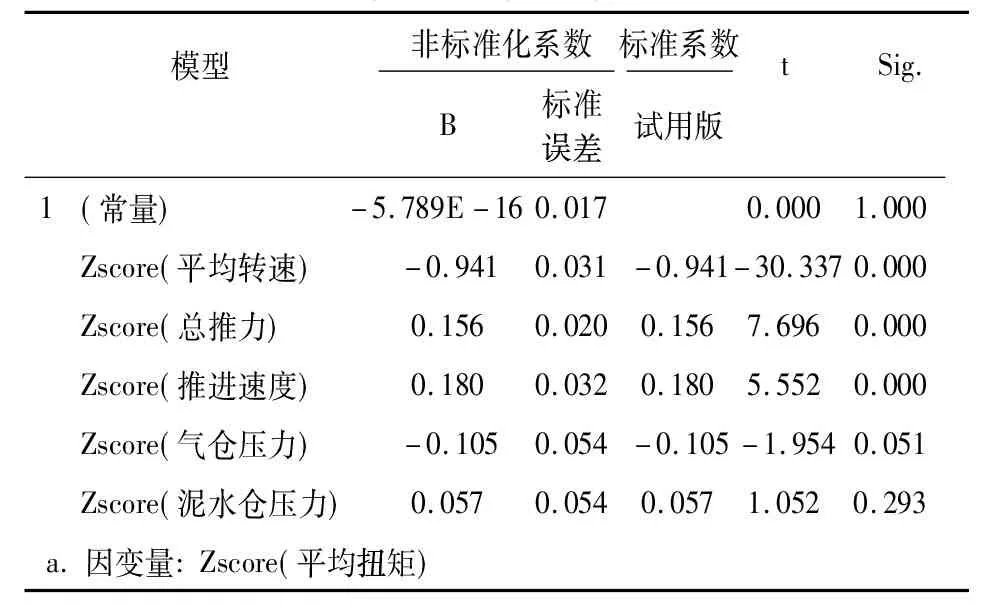
表7　回归系数a

表中，非标准化系数的B列列出了α、β1、β2、β3、β4、β5求解出的具体数值。因此总推力的多元线性表达式为：

F=-5.789×10-16-0.941X转+0.156X推+0.18X速-0.105X气+0.057X泥

(3-5)

3.4总推力的多元线性回归模型的精度分析

同样，由于盾构参数和扭矩之间存在相关性并不代表该施工参数对掘进速度的影响一定显著，所以还需结合t检验进行分析对上述表达式进行精度分析。t值检验的结果即为上表的最后两列。

从表格中可以看出，仅平均转速、总推力和推进速度t检验的p值小于0.05，说明仅平均扭矩和总灌浆量对总推力的偏回归系数达到极显著水平。气仓压力t检验的p值为0.051，略大于0.05，在可以接受的范围之内，将其纳入显著变量。剔除不显著变量，仅以平均转速、总推力、推进速度和气仓压力为变量，重新对总推力的多元线性回归模型进行回归分析。

首先依然要对调整后的多元线性回归模型进行显著性分析，F检验结果如表8。从表8可以看出，F检验的p值小于0.05，故调整后的多元线性回归模型通过了显著性检验。

表8方差分析b

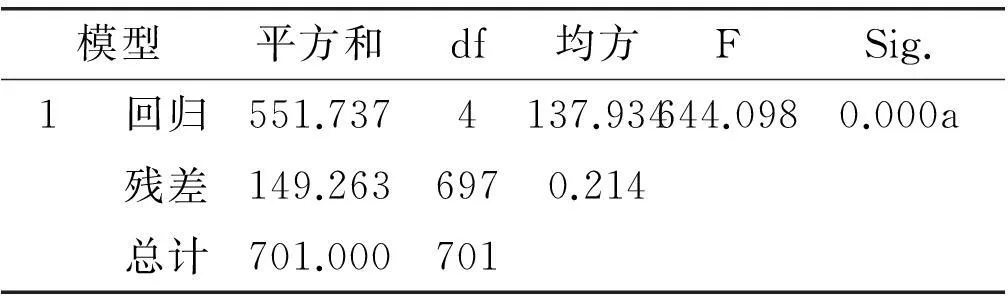
模型平方和df均方FSig.1回归551.7374137.934644.0980.000a残差149.2636970.214总计701.000701

同样对标准化后的数据进行多元线性回归分析，得到回归系数表9。

表9回归系数a

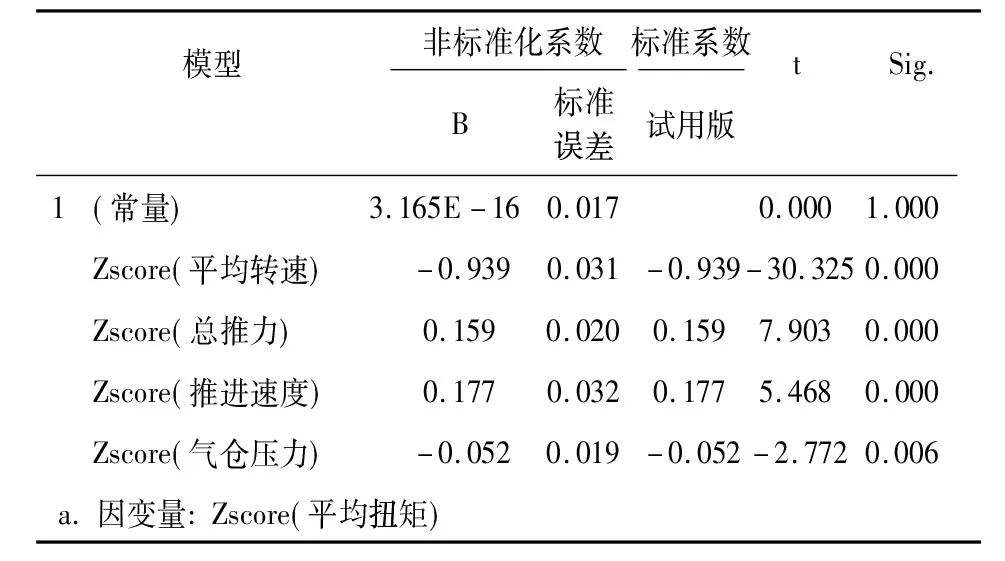
模型非标准化系数标准系数tSig.B标准误差试用版1(常量)3.165E-16 0.0170.0001.000Zscore(平均转速)-0.9390.031-0.939-30.3250.000Zscore(总推力)0.1590.0200.1597.9030.000Zscore(推进速度)0.1770.0320.1775.4680.000Zscore(气仓压力)-0.0520.019-0.052-2.7720.006a.因变量:Zscore(平均扭矩)

从表9中可以看出，平均转速、总推力、推进速度和气仓压力均达到显著水平。因此，调整后的多元线性回归表达式为：

N=-0.939+0.159X推+0.177X速-0.052X气

(3-6)

4结论

本研究以武汉地铁4号线作为研究背景，采用757环到1460环的左线泥水盾构施工报告数据，利用多元线性回归法对施工报告数据进行分析，最终得到如下结论：

(1)根据求解出的总推力多元线性回归模型，虽然和总推力显著相关的盾构参数有6个，但真正对总推力影响最大的只有4个，分别是平均转速、平均扭矩、总灌浆量和推进速度。这四个变量中，平均转速和平均扭矩与总推力呈正相关，推进速度和总灌浆量与总推力呈负相关。

(2)由求解出的平均扭矩多元线性回归模型知，真正对平均扭矩影响最大的参数也只有4个，分别是平均转速、推进速度、总推力和气仓压力，其中，平均转速和气仓压力与平均扭矩呈负相关，推进速度和总推力与平均扭矩呈正相关。

(3)本研究得出的总推力模型和扭矩模型虽然能在某种程度上表现出实际施工情况；但在实际施工过程中盾构施工效率还会受到地质条件、盾构施工组织、设备状况、资源供应、等的影响使得模型的精度还有待提高，未来的研究也可以致力于提高本模型的精度，进而使本模型能更有效地指导施工。

参考文献

[1] 国家住建部.2014年城乡建设统计公报.[R/OL].[2015- 07-03].http：//www.mohurd.gov.cn/wjfb/2015 07/t20150 703_222769.html.

[2]周诚.地铁盾构施工地表变形时空演化规律与预警研究[D].华中科技大学，2011.

[3]蒋洪进.泥水盾构穿越既有隧道的影响及施工参数研究[D].上海交通大学，2009.

[4]朱宏伟.泥水盾构掘进速度的影响因素及数值分析[J].现代城市轨道交通，2008(4)：39-41.

[5]Bruines P.A..The use of a rock mass classification scheme for tunnel boring machines[A].In：Adachi Swets，Zeitling ered.Modern Tunneling Science and Technology[C].[s.1.]：[s：n]，2001，583-588.

Multivariate Linear Regression Analysis of Slurry Shield Construction Parameters

Liao Lizhao1，Tao Ye2,Liu Hui2

(1.ShanghaiTianyouEngineeringConsultingCo.，Ltd.，Shanghai200092，China； 2.SchoolofCivilEngineering&Mechanics，HuazhongUniversityofScience&Technology，Wuhan430074，China)

Abstract:Shield construction technology is widely used in the construction of the subway engineering，but at present，domestic and foreign studies on shield tunneling parameters are comparatively less,among which most is about EPB shield.Research on multiple linear regression analysis of slurry shield construction parameters has become almost an empty field.Therefore，it is necessary to study multiple linear regression analysis slurry shield construction parameters to ensure the safety of the construction process and to reduce project cost as well as the adverse impact of subway construction.This article takes the example of the 757 to 1460 of the left line of shield construction data of Wuhan metro line 4，uses SPSS statistical software for statistical data analysis and establishes the multiple linear regression models of the total thrust and torque.The multiple linear regression models can be used to predict the total thrust and torque of the construction.With the right line shield construction field data for engineering verification，it is found that the predicted results are in good agreement with the actual results.

Key Words：Slurry Shield；Shield Parameters；Statistical Analysis；Linear Regression；Predict

【基金项目】国家自然科学基金“基于复杂网络理论的地铁盾构施工诱发环境风险的时空演化机理与规律研究”(编号：51408245)

【作者简介】廖利钊(1962-)，男，高级工程师。主要研究方向：地铁工程风险控制。

【中图分类号】U455.43

【文献标识码】A

【文章编号】1674-7461(2016)03-0096-06