关于复积分的计算

袁邢华，蒋巧云（南通大学 理学院，江苏 南通 226019）



关于复积分的计算

袁邢华，蒋巧云
（南通大学 理学院，江苏 南通 226019）

摘要：通过一个具体复积分实例，讨论了复积分的计算问题，总结了复积分的多种计算方法，以此加强学生对相应主要知识点的理解和掌握.

关键词：复积分；柯西积分公式；留数

在复变函数论中，复积分的计算是比较重要的一个内容［1-3］.本文通过一个具体的实例给出它的多种解法，从而让学生更好地理解和掌握复变函数中几个重要的知识点，而且通过一题多解，也让学生对这些知识点之间的联系有了更加全面的认识.

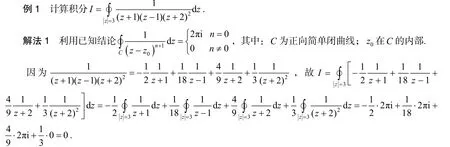
解法1比较适合被积函数是有理分式且比较容易进行部分分式分解的积分，另外，对所用到的已知结论要比较熟悉.关于如何对有理分式进行分解详见文献［4］.

解法2 利用复合闭路定理、柯西积分公式和高阶导数公式.

在z =3的内部作正向简单闭曲线C1，C2，C3，使得-1在C1内部，1在C2内部，-2在C3内部，并且C1，C2，C3互不相交，互不包含，从而

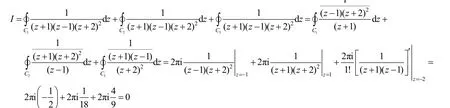
解法2的特点是不用把被积函数部分分式分解，而只需作适当变形让其满足柯西积分公式或高阶导数公式的要求，进而利用公式即可.

解法3 利用留数定义.

解法3对例1来讲计算时不是太简单，但如果被积函数在积分曲线内部的奇点是本性奇点时就只能用此方法来处理了.

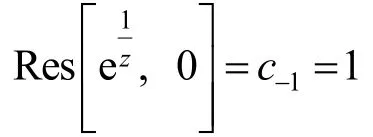
解法4 利用留数定理及关于极点的留数计算规则.

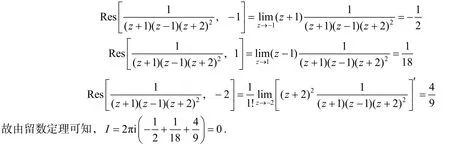
解法4比较适合被积函数的奇点是极点，而且极点级数不超过三级的积分.

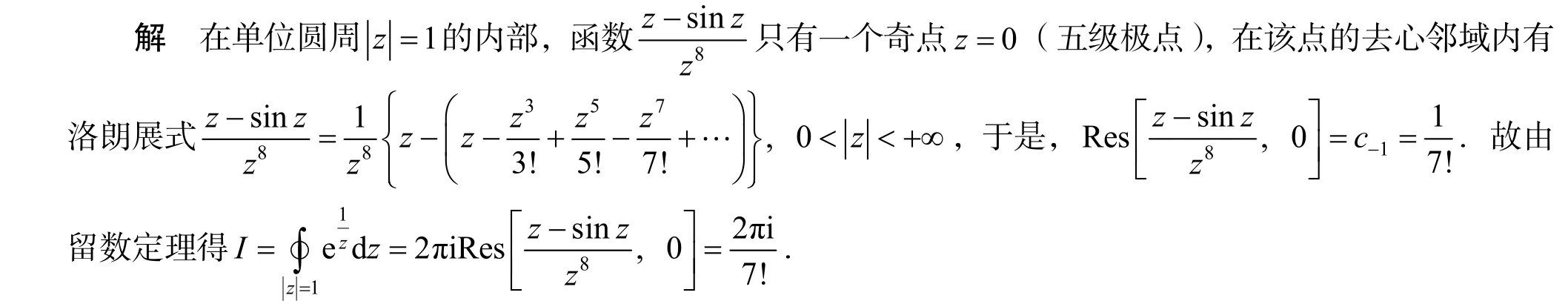
留数总和定理［5］如果函数f（z）在扩充复平面内只有有限个孤立奇点，那么f（z）在所有奇点（包括∞点）的留数的总和必等于零. 0 .

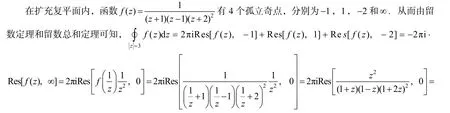
解法5比较适合积分曲线内部出现多个奇点，而且有些奇点处留数的计算又比较复杂时的积分，通过留数总和定理的转化，可以把计算留数变得相对简单.

通过本文的讨论，希望在今后的教学过程中更加全面深入地讲解这部分知识，激发学生的学习兴趣，帮助学生更好地理解和掌握这部分内容，灵活地运用这些方法来计算复积分.

参考文献：

［1］ 钟玉泉.复变函数论［M］.3版.北京：高等教育出版社，2004

［2］ 余家荣.复变函数论［M］.3版.北京：高等教育出版社，2000

［3］ 路见可，钟可寿.复变函数论［M］.2版.武汉：武汉大学出版社，2007

［4］ 同济大学应用数学系.高等数学［M］.5版.北京：高等教育出版社，2002

［5］ 吕彦鸣.复变函数［M］.北京：化学工业出版社，2010

重 要 声 明

为扩大本刊及作者知识信息交流渠道，加强知识信息推广力度，本刊已许可中国学术期刊（ 光盘版） 电子杂志社在 CNKI 中国知网及其系列数据库产品中，以数字化方式复制、汇编、发行、信息网络传播本刊全文。该著作权使用费及相关稿酬，本刊均用作为作者文章发表、出版、推广交流（ 含信息网络） 以及赠送样刊之用途，即不再另行向作者支付。凡作者向本刊提交文章发表之行为即视为同意我刊上述声明。

《高师理科学刊》编辑部

About the calculation of complex integral

YUAN Xing-hua，JIANG Qiao-yun
（Shool of Science，Nantong University，Nantong 226019，China）

Abstract：Through a complex integral example，discussed the calculation problem and summarized the various calculation methods of complex integral，then to strengthen students' understanding and mastery of corresponding main knowledge points.

Key words：complex integral；Cauchy integral formula；residue

中图分类号：O174.5∶G642.0

文献标识码：A

doi：10.3969/j.issn.1007-9831.2016.05.014

文章编号：1007-9831（2016）05-0048-03

收稿日期：2016-02-20

基金项目：南通大学教学改革课题（2014B7）

作者简介：袁邢华（1978-），男，江苏海门人，讲师，硕士，从事复变函数研究.E-mail：ntsandy2004@ntu.edu.cn