不同耦合方式对单个振荡系统中螺旋波的影响

赵瑞，李樊

（1. 中国地震局地震研究所 地震大地测量重点实验室，湖北 武汉 430071；2. 湖北省地震局，湖北 武汉 430071；3. 襄阳市中心医院 急诊科，湖北 襄阳441021）



不同耦合方式对单个振荡系统中螺旋波的影响

赵瑞1，2，李樊3

（1. 中国地震局地震研究所 地震大地测量重点实验室，湖北 武汉 430071；2. 湖北省地震局，湖北 武汉 430071；3. 襄阳市中心医院 急诊科，湖北 襄阳441021）

摘要：研究不同耦合方式对振荡介质中螺旋波的影响，同时用可激发介质中的螺旋波作为对比.结果表明，不同耦合方式对螺旋波的影响主要表现为波纹、周期和振幅的变化，如螺旋波进入时空混沌，平均振幅变大，相邻的周期变小.

关键词：振荡系统；耦合；静息态

自非线性科学形成以来，螺旋波斑图备受关注，尤其是心脏中的螺旋波，主要造成心律不齐和心动过速.目前主要有化学实验法、物理法和数值模拟3种研究方法.使用最多的是数值模拟，利用计算机编程，离散非线性模型，采取合理的边界条件和初始条件，从而再现螺旋波的特性.合理有效地控制螺旋波，可以防止螺旋波失稳破碎，形成时空混沌，而进一步破坏心脏的有机组织.目前控制方法主要有：（1）全局控制，像外加周期信号，驱动耦合；（2）局部控制，如参数扰动等.其中张宏［1］通过周期地注入外界信号抑制螺旋波和时空混沌；马军［2］通过外界电场控制螺旋波和时空混沌；Nekorkin等人［3-5］利用耦合方法控制螺旋波和时空混沌.钱郁［6］对激发介质中螺旋波做了长程连接的研究.

截止到目前为止，采用驱动耦合方法控制螺旋波主要集中在激发介质中，而对于振荡介质中的螺旋波，以及单层的耦合研究的不够多.

1　模型

二维的复金兹堡-朗道方程［7-8］其表达式（1）

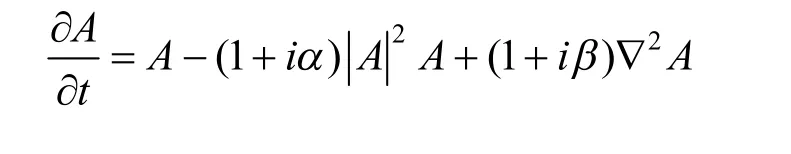
其中：A是系统的复变量，具有A=a +ib 的形式，二阶偏导数可以写成▽2A =（∂2A/∂x2）+（∂2A/∂y2）.微调2个主要参数α和β时，可以绘制出各种各样的时空斑图，螺旋波斑图就是其中的一种.已有的研究表明，当αβ≥0（α＞β≥0或者0≥β＞α）时会出现反螺旋波［9］.同时又有结果表明，当α＜β时系统才会出现反螺旋波［10］.

数值模拟中把参数α，β分别设置为α=0.35和β=-1.36，数值模拟的区域大小设置为100×100，离散成256×256的格点.使用无流边界条件，一阶欧拉向前差分，五点差分近似方法分别作用在系统的边界.时间和空间上，空间步长取Δx=Δ y=1.0，时间步长Δt=0.05，合理的设置初始条件振荡系统会出现稳定的螺旋波.

2　数值模拟方法

在单层振荡系统中，采用点对点的耦合方法，每个格点的选取都有一定的选择概率，同时在数值模拟中不会出现重复选中.为了具体研究螺旋波，数值模拟主要从以下2个角度出发：

（1）在数值模拟的整个过程中，固定性的选择1对耦合格点；

（2）在数值模拟中设置一定的选择概率p，不同时间无重复的选择需要耦合的2个格点.

数值模拟中以稳定旋转的螺旋波作为耦合前的初始态，耦合项在稳定态之后加入.本文以18 000个时间步长为准，耦合示意图见图1.

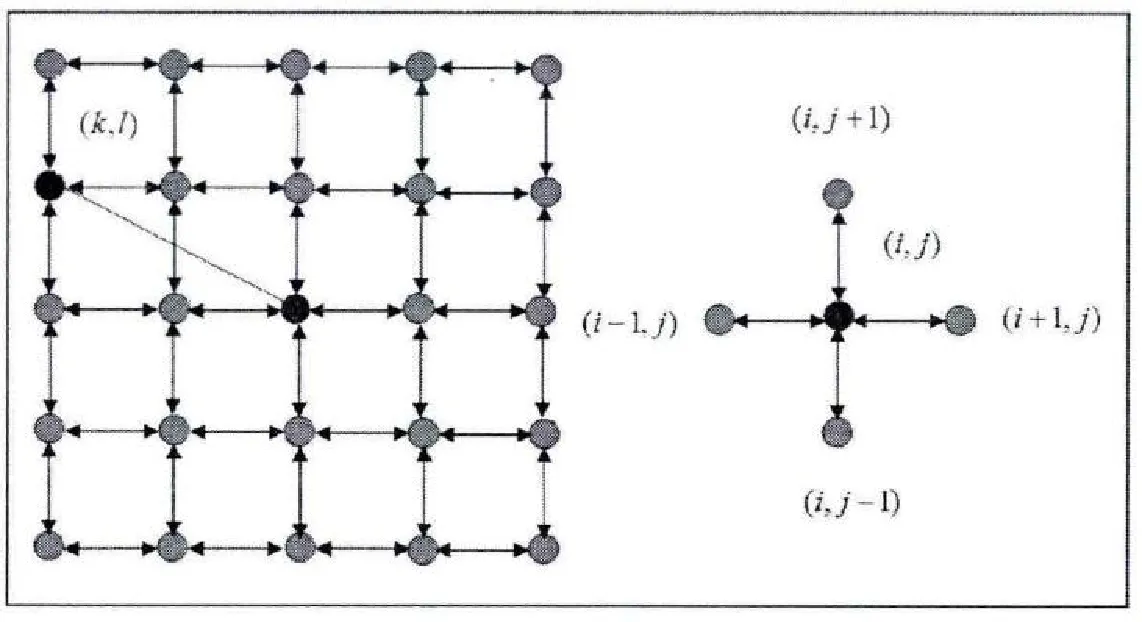
图1 耦合示意图

3　数值结果与分析

根据给出的耦合方法，主要研究2种耦合方式对单个振荡系统中螺旋波动力学行为的影响，主要从斑图的演化和部分的数学参量变化情况来描述.

3.1固定耦合

首先选取复变量耦合格点A（128，128）和A（192，192）作为耦合的对象，当整个平面空间被螺旋波占据时，加入此耦合项，振荡介质和激发介质中螺旋波受到此连接后的变化情况见图2和图3.

从图2和图3中可以发现，稳定的螺旋波波纹变细，周围出现少量的混沌，中心伴随着静息态，长时间演化，系统最终转变为稳定的静息态.应用到不同的介质中，例如：可激发介质［11-12］，同样将螺旋波转化为静息态，不仅需要的时间少，而且不会引起时空混沌.

3.2随机耦合

随机性的耦合，简单的说就是以一定的概率p随机性的，并且没有重复性的从离散格点中只选择1对格点作为耦合项加入动力学方程中的右边.不同选择概率p对整个螺旋波斑图演化的影响见图4.

选择概率p =0.2的情况下螺旋波的变化情况见图5.从图4、图5可以发现，随机性耦合不仅可以促使螺旋波的破碎，而且又引导其进入时空均匀的静息态.

图2 振荡介质中螺旋波的演化

在非线性物理中，一般利用自关联函数来度量系统本身各个格点的同步状态.例如：文献［4］使用全局偏导数来描述控制方法的效果，得到的变化关系图见图6.其参数表示为

加入耦合前后系统的平均振幅随时间的变化情况见图7，其中图7a是未加入耦合的关系图（p =0.0），图7b是加入耦合后的关系图（p =0.2）.由图7可以发现，二者周期和振幅之间有一定的区别，加入随机耦合致使系统出现混沌，而引起整个系统的平均振幅和周期发生了变化.

图3 激发介质中螺旋波的演化

图4 不同概率下螺旋波的演化

图5 概率p =0.2的情况下螺旋波的演化

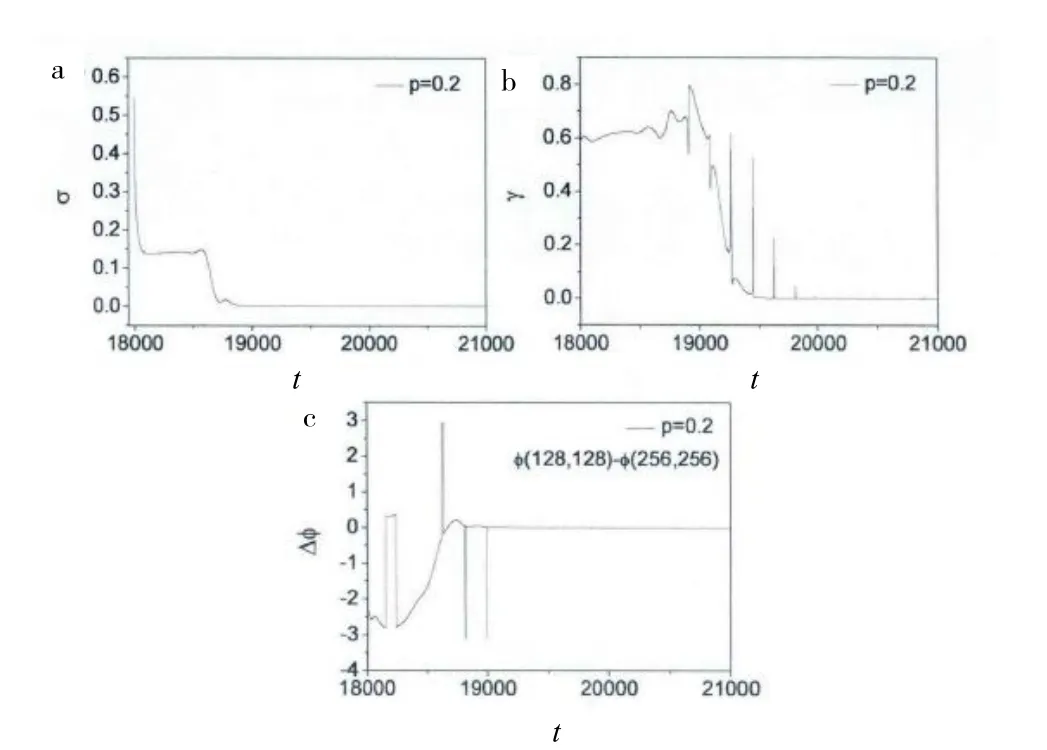
图6 相关参数的变化

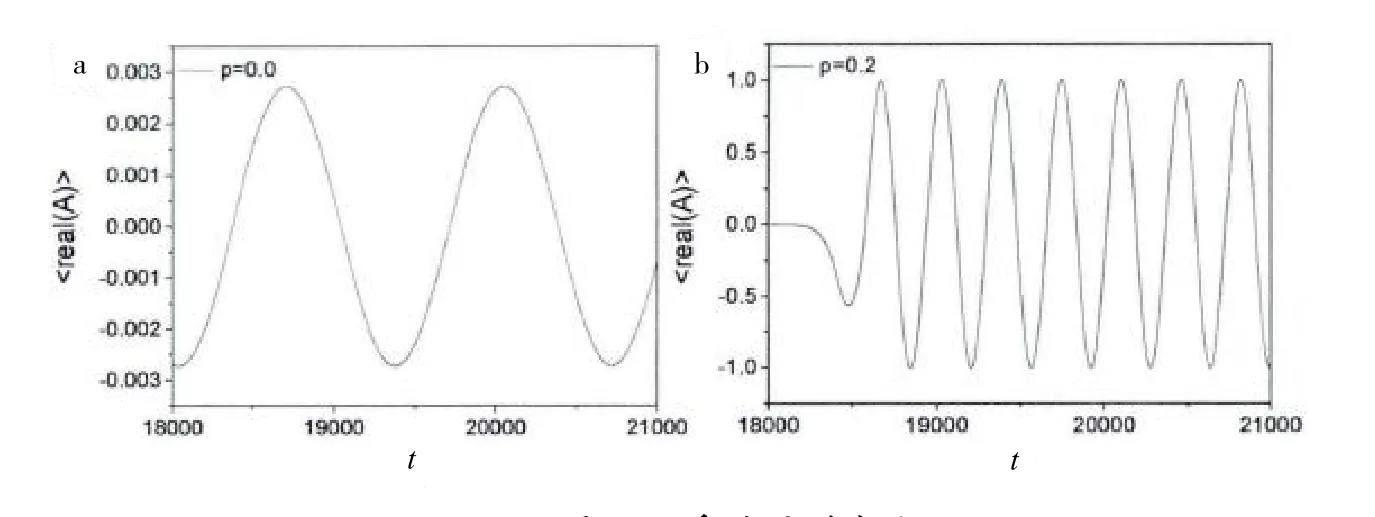
图7 瞬时平均振幅

4　结论

以一定的选择概率p来设置动力学系统的耦合项，讨论单个振荡系统中螺旋波演化的特性，得出结论：（1）无论在振荡介质还是激发介质中，都可以选择利用确定性的耦合抑制系统中的螺旋波和时空混沌，唯一的区别就是在振荡介质中需要的控制时间比激发介质中的要长；（2）随机耦合会引起振荡介质中的螺旋波破碎，但最终随着控制时间的推移同样可以控制其进入时空均匀的静息态；（3）随机耦合通过2个格点的耦合来影响整个系统的幅度，但相邻格点的周期变小了.

参考文献：

［1］ Zhang H，Hu B，Hu G.Suppression of spiral waves and spatioteporal chaos by generating target waves in excitable media［J］.Physical Review E，2003，68（2）：026134-1-026134-4

［2］ Ma J，Ying H P，Li Y L.Suppression of spiral waves using intermittent local electric shock［J］.Chinese Physics，2007，16（4）：0955-0961

［3］ Nekorkin V I，Kazantsev M G，Velarde M G，et al.Pattern interaction and spiral waves in a two-layer system of excitable

units［J］.Physical Review E，1998，58（2）：1764-1773

［4］ 邝玉兰，唐国宁.心脏中的螺旋波和时空混沌的抑制研究［J］.物理学报，2012，61（10）：100504-1-100504-8

［5］ Zhao R，Pan W，Xue Y.Exploring the control of spiral waves and spatiotemporal chaos by stochastic and cross-coupling

method［J］.Ineternational Jounal of Modern Physics B，2013，27（23）：1350129-1-1350129-9

［6］ Qian Y.The influence of long-range links on spiral waves and its application for control［J］.Chinese Physics B，2012，21（8）：088201-1-088201-7

［7］ Aranson I S，Kramer L.The word of the complex Ginzburg-Landau equation［J］.Reviews Modern of Physics，2002，74（1）：99-143

［8］ 高继华，谢伟苗，高加振，等.耦合复金兹堡-朗道（Ginzburg-Landau）方程中的模螺旋波［J］.物理学报，2012，61 （13）：130506-1-130506-6

［9］ Gong Y F，Christini D J.Antispiral waves in reaction-diffusion systems［J］.Physical Review Letters，2003，90（8）：088302-1-088302-4

［10］ Brusch L，Nicola E M，Bär M.Comment on“Antispiral waves in reaction diffusion systems”［J］.Physical Review Letters，2004， 92（8）：089801-1

［11］ Bär M，Eiswirth M.Turbulence due to spiral breakup in a continuous excitable medium［J］.Physical Review E，1993，48（3）：1635-1637

［12］ Bragard J，Vidal G，Mancini H L，et al.Chaos suppression through asymmetric coupling［J］.Chaos，2007，17（4）：043107-1-043107-8

优先数字出版声明

为了提高学术成果传播和利用价值，对具有创新性的科研成果争取首发权，《高师理科学刊》已成为“中国知网”、“万方数据”优先数字出版期刊.

优先数字出版平台是快速实现各学术期刊论文按篇即时在线出版的平台，其功能是切实提高学术期刊文献出版的时效性和影响力.该平台以印刷版期刊录用的稿件为内容，本刊编辑部在得到作者授权后，将对国家自然科学基金项目，省、部级自然基金项目及教学研究项目等符合优先数字出版条件的优质稿件进行优先处理，快速实现单篇即时在线出版（等同纸质出版）.自数字出版之日起，登录中国知网（CNKI）全文数据库和万方数据库可全文检索和下载优先出版的稿件.

《高师理科学刊》编辑部

The influence of different coupling methods for spiral waves in single oscillation system

ZHAO Rui1，2，LI Fan3
（1. Key Laboratory of Earthquake Geodesy，Institute of Seismology，CEA，Wuhan 430071，China；2. Earthquake Administration of Hubei Province，Wuhan 430071，China；3. Department of Emergency，The Central Hospital of Xiangyang City，Xiangyang 441021，China）

Abstract：Study the influence of different coupling methods on the spiral waves in oscillation system. By comparing the excitable media，the research results show that the wave，period and amplitude are major impacts for the different types of coupling，such as the spiral waves are come into the spatiotemporal chaos，the mean amplitude is increased and the adjacent peak period is shortened.

Key words：oscillation system；coupling；resting state

中图分类号：O415.5

文献标识码：A

doi：10.3969/j.issn.1007-9831.2016.05.008

文章编号：1007-9831（2016）05-0023-04

收稿日期：2016-03-10

作者简介：赵瑞（1985-），男，湖北襄阳人，工程师，硕士，主要从事计算物理与非线性物理方面的研究.E-mail：zhaorui0612@163.com