关于不定方程x3-1 = Dy2

杨雅琴

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）



关于不定方程x3-1 = Dy2

杨雅琴

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）

摘要：利用参数法将不定方程x3-1 = Dy2（D＞0）分解成一元一次方程和一元二次方程组成的方程组，对这个方程组的解用参数表示，通过设定此参数的值得到该不定方程的非平凡解.分别讨论D不可约和D可约时，不定方程x3-1 = Dy2非平凡解的求解方法.

关键词：参数法；不定方程；非平凡解

1 引言及预备知识

关于不定方程x3-1 = Dy2（D＞0）已经有不少的研究成果.当D无6k + 1的素因数时，其全部整数解已由曹珍富［1］等得到.但当D有6k + 1的素因数时，方程的求解较为困难，许多学者对其进行了研究［2-8］.本文将不定方程x3-1 = Dy2分解成一元一次方程和一元二次方程组成的方程组，对这个方程组的解用参数表示，通过设定此参数的值得到该不定方程的非平凡解.分别讨论D不可约和D可约时，不定方程x3-1 = Dy2非平凡解的求解方法，给出不同D值对应的不定方程x3-1 = Dy2的非平凡解.

对于任意的D＞0，不定方程x3-1 = Dy2都有平凡解（1，0）.讨论当D＞1时，不定方程x3-1 = Dy2非平凡解的存在情况.

引理［3］20设p是一个素数，则不定方程u2-4 Dv2=± p 至多有一个解.

定理1 当D为偶数时，不定方程u2-4 Dv2= - 3无整数解.

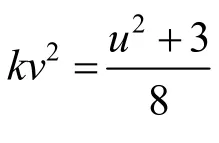
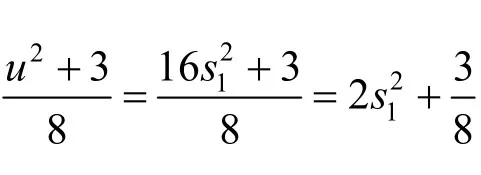
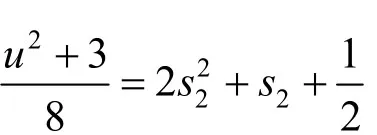
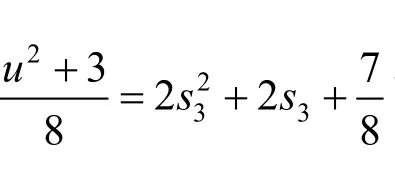
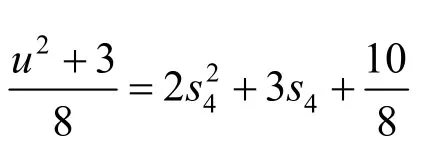
为非零整数，则（u2+3）≡0（mod4），那么，u必为奇数.

如果v为偶数，则存在整数s，使得v=2 s，那么，不定方程u2-4 Dv2= - 3可写成u2-16 Ds2= - 3 .由定理1可知，不定方程u2-16 Ds2= - 3中（u，s）无整数解，与已知矛盾.所以，v必为奇数.再由引理可知，如果不定方程u2-4 Dv2= - 3有整数解（u，v），则此不定方程只存在唯一一组整数解. 证毕.

2 D不可约时，不定方程x3-1 = Dy2的非平凡解

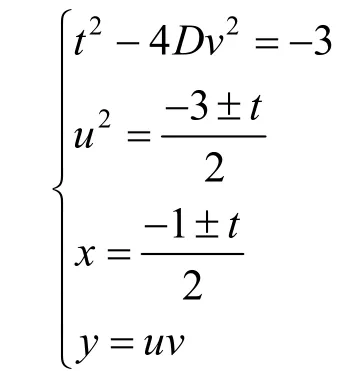
（1）21x- = Du，221 x+x+v=，y= uv；

（2）21x- = u，221 x+xD+v=，y= uv；

（3）213x- = u，2213 xxDv + + =，y=3 uv；

（4）213x Du - =，2213 xxv++=，y=3 uv .

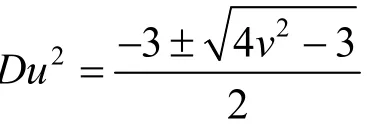
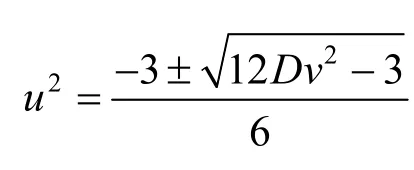
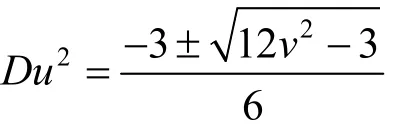
综上可知，不定方程x3-1 = Dy2（D是不可约的正整数）的非平凡解（x，y）满足方程组

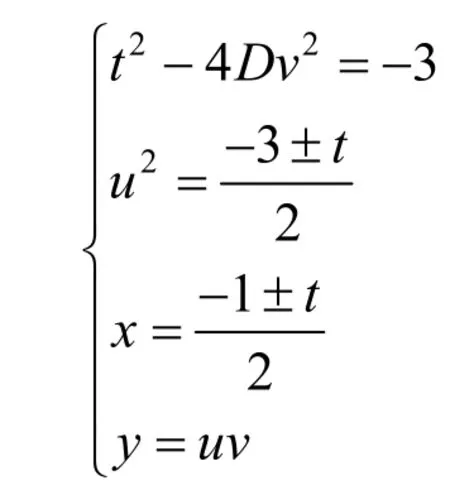
（t为奇数参数）或

（t为奇数参数）证毕.

例1 求不定方程x3+1 = 307y2的非平凡解.

例2 求不定方程x3+1 = 271y2的非平凡解.

解 因方程组有解，则不定方程x3+1 = 1801y2的非平凡解为（28，±9）.

3　构建x3-1= Dy2并求解

4　D可约时，不定方程x3-1= Dy2的非平凡解

设存在非零整数m，n，使D= mn .此时不定方程x3-1 = Dy2有2种可能的分解：

（1）x-1 =mu2，x2+ x +1 = nv2，y = uv 或x-1 = nu2，x2+ x +1 = mv2，y = uv ；

（2）x-1 =3mu2，x2+ x +1 = 3 nv2，y=3 uv 或x-1 = 3 nu2，x2+ x +1 =3 mv2，y=3 uv .

当D可约时，由给定不定方程的非平凡解可以推出其他不定方程的非平凡解.如不定方程x3-1 = 124y2的非平凡解为（5，±1），由于124= 31×+4，则x3-1 = 31y2的非平凡解为（5，±2）.

参考文献：

［1］ 曹珍富.丢番图方程引论［M］.哈尔滨：哈尔滨工业大学出版社，1989：209-213

［2］ 段辉明.关于丢番图方程x3+1 = 37y2［J］.高师理科学刊，2009，29（5）：22-25

［3］ 柯召，孙琦.谈谈不定方程［M］.上海：上海教育出版社，1980：18-35

［4］ 潘承洞，潘承彪.初等数论［M］.2版.北京：北京大学出版社，2003：271-303

［5］ Kenneth H R.初等数论及其应用［M］.北京：机械工业出版社，2009：98-103

［6］ 高洁，袁进.关于Diophantine方程x3+1 = py2［J］.纯粹数学与应用数学，2010，26（4）：687-690

［7］ 高洁，梁勇.关于Diophantine方程x3-1 = py2［J］.科学技术与工程，2010，10（18）：4461-4462

［8］ 牟善志，戴习民.关于丢番图方程x3±1= py2［J］.安徽大学学报：自然科学版，2008，32（1）：18-20

On the Diophantine equationx3-1 = Dy2

YANG Ya-qin
（School of Science，Qiqihar University，Qiqihar 161006，China）

Abstract：Use parameter method，gave decomposition of the diophantine equationx3-1 = Dy2（ D ＞0）to one simple equation and one consisting of a quadratic equation equations.The parameters is used in the solution of equations，set the parameter to obtain the non-trivial solution of indeterminate equation.Discusses the method for solving non-trivial solution ofx3-1 = Dy2when D is irreducible or reducible.

Key words：parametric method；Diophantine equation；non-trivial solution

中图分类号：O156.1

文献标识码：A

doi：10.3969/j.issn.1007-9831.2016.05.001

文章编号：1007-9831（2016）05-0001-04

收稿日期：2016-01-10

作者简介：杨雅琴（1971-），女，吉林洮安人，副教授，硕士，从事组合数学研究.E-mail：yyqcpy2008@126.com.