三相对称系统中SVC-MERS注入谐波电流分析

程苗苗，包跃跃，涂春鸣，张忠杰，刘治国

（湖南大学电气与信息工程学院，长沙410082）

DOI：10.13234/j.issn.2095-2805．2016．1．10中图分类号：TM 46文献标志码：A

三相对称系统中SVC-MERS注入谐波电流分析

程苗苗，包跃跃，涂春鸣，张忠杰，刘治国

（湖南大学电气与信息工程学院，长沙410082）

磁能恢复开关MERS（magnetic energy recovery switch）是一种新型的无功补偿装置，它相较于其他无功补偿装置，具有结构简单、易于控制和损耗低等诸多优点，但在进行无功功率补偿的过程中会产生谐波电流。首先，在对MERS的结构和控制方法阐述的基础上建立了三相对称系统中SVC-MERS的数学模型，讨论分析了控制参数对三相对称系统中线电流谐波特性的影响；进而提出了控制参数的优化设计方法。仿真和实验结果表明，通过控制参数的优化设计可以有效地减小三相对称系统中线电流的谐波含量，所提控制参数的优化设计方法是可行的。

三相对称系统；并联无功补偿；磁能恢复开关（MERS）；谐波电流

Project Supported by National Natural Science Foundation of China（51307048）；Hunan Provincial Science and Technology Project（2015WK3004）

引言

无功功率补偿对于稳定电网电压、调节功率因数以及平衡感性负载都具有十分重要的意义。通过无功补偿装置对输电线路进行功率补偿能够最大限度地减少电网损耗和改善电网的质量。随着电力电子技术的快速发展，研究人员已经研发出各种基于电力电子开关器件的静止无功补偿器SVC（static switched capacitor）。其中，晶闸管投切电容器TSC （thyristor switched capacitor）、晶闸管控制电抗器TCR（thyristor controlled reactor）等都是应用相当普遍的无功补偿装置［1］。TSC具有损耗低、谐波含量小等优点，但其缺点是只能进行阶段性的容性无功补偿，无法实现最佳补偿；TCR虽然能够实现感性无功功率的连续补偿，但是不符合电网系统或者电力设备大多需要补偿容性无功功率的实际需求。静止同步补偿器STATCOM（static synchronous compensator）是近年来无功补偿装置的研究热点，它既能够连续调节容性无功功率的输出，又能连续调节感性无功功率的输出，然而对于工业应用来说，STATCOM的控制系统过于复杂，而且价格昂贵［2］。

目前，磁能恢复开关MERS（magnetic energy recovery switch）作为一种新型的静止无功补偿装置，已经引起了研究者的广泛兴趣。它具有结构简单、电容小、低损耗、能够连续无级地调节输出容性无功功率等诸多优点。MERS的基本工作原理是通过控制开关器件的通断时间来改变接入系统中的电容容抗的大小，从而实现输出容性无功功率的连续调节。MERS作为一种可控串联补偿技术在控制电力潮流，补偿线路感抗压降等方面都得到了广泛的研究和证明。然而，在MERS用作并联型静止无功补偿器即SVC技术的研究还很少，其工作特性还有待进一步地明确。

针对这种情况，本文主要研究MERS用作静止无功补偿器SVC时的工作特性，重点对SVC-MERS在三相对称系统条件下的注入电流谐波特性进行了理论分析和实验研究［3］。首先，本文阐述了SVCMERS的主要控制策略，并对全桥型和半桥型SVCMERS作了简单的对比；其次，通过建立三相对称系统中SVC-MERS的数学模型，分析三相对称系统中SVC-MERS接成三角形连接时系统注入电流谐波特性，明确了控制参数在该连接条件下对线电流谐波含量的影响，在此基础上，提出控制参数的优化设计方法；最后，通过仿真和实验进行验证。

1　SVC-MERS的控制策略

1.1MERS的典型结构拓扑以及基本控制原理

典型的MERS有3种结构：全桥型MERS、逆导型IGBT半桥型MERS和逆阻型IGBT半桥型MERS，其拓扑结构如图1所示。其中，图（a）为全桥型MERS，开关器件数量是4个，理论上可控电容容抗的调节范围为0～∞；图（b）和图（c）为半桥型MERS，开关器件的数量是全桥型MERS的一半，理论上可控电容容抗的调节范围是从0～XC，其无功补偿范围可视为全桥型结构的一半。半桥型MERS有2种形式，二者的区别在于图（c）采用了逆阻型IGBT，具有更低的电压导通压降，从而导通损耗更小。

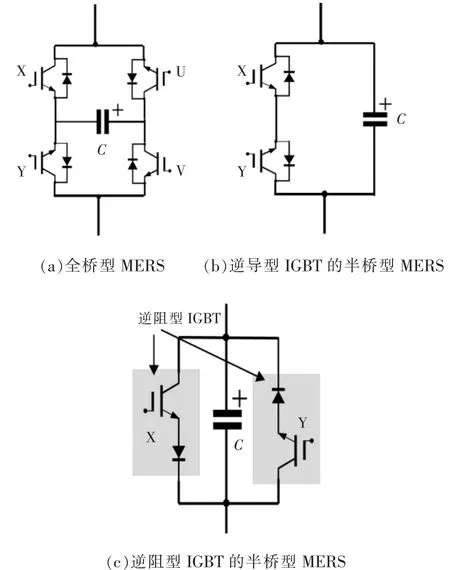
图1　MERS的拓扑结构Fig.1 MERS topology structure

1.2MERS用作SVC技术的控制方法

MERS的基本工作原理是通过控制开关器件的开通和关断，实现对接入系统的电容容抗的连续调节，即可等效为一个可变电容。各种MERS结构单元并联在系统中用作静止无功补偿即称为SVCMERS技术，通常在MERS和电网系统中间串联一个电感，其目的是为了抑制接入MERS的冲击电流和降低电流的谐波含量。基于全桥型MERS单元和基于半桥型MERS单元的单相SVC-MERS结构如图2所示。

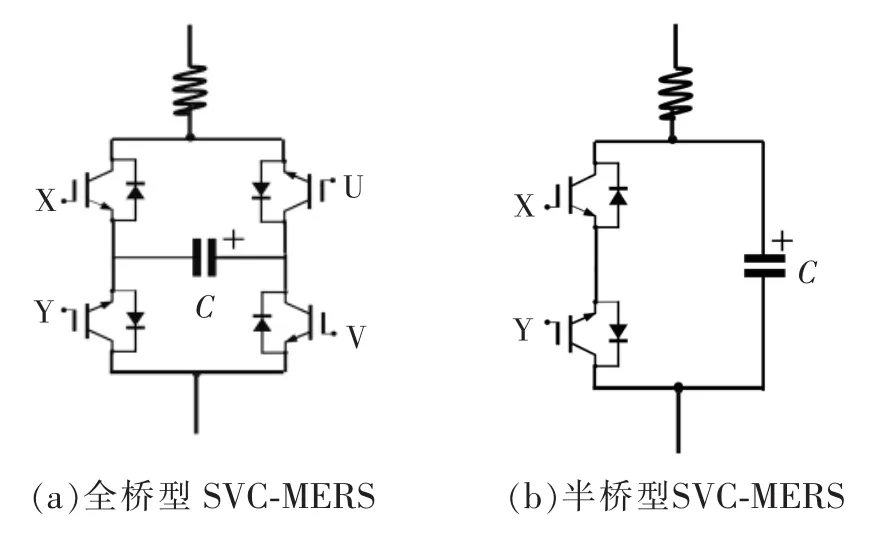
图2　SVC-MERS结构Fig.2 Configuration of SVC-MERS

SVC-MERS的基本控制思想在于通过控制MERS的发生电压波形来调节输出的容性无功功率的大小。图3为全桥型SVC-MERS的电流路径及其基本工作原理。一个完整的工作周期包含了6个阶段，分别对应2种电流流向时的电容充电（charging）、放电（discharging）和旁路（single bypass）状态。在系统以及装置参数一定的条件下，SVC-MERS的发生电压波形取决于γ和VCmin这2个控制参数，其中γ是指电源电压与开关信号之间的相位差；VCmin是指在稳定运行状态下电容电压的最小值。随着γ和VCmin的变化，SVC-MERS的发生电压波形表现为以下3种情况：（1）不连续模式（distinuous mode）：γ＞0，VCmin=0时，SVC-MERS电压不连续，在每一周期的一段时间内为0 V，此时，对应的MERS等效电抗XMERS＜XC；（2）直流偏置模式（dc-offset mode）：γ=0，VCmin≥0时，MERS内置的电容两端电压的最小值大于等于0 V，此时，对应的MERS等效阻抗XMERS≥XC；（3）直流偏置-旁路模式（dcoffset-bypass mode）：γ＞0，VCmin＞0时，MERS内置电容的电压在每一周期内保持在VCmin电压值一段时间，此时，对应的MERS等效阻抗XMERS要根据具体控制参数γ和VCmin判断是否比XC大或者小。其中，XC为MERS的内置电容阻抗，XMERS为MERS的等效阻抗［4-10］。可见，通过改变2个控制参数γ和VCmin的大小，可以实现等效容抗从0到无穷大的连续可调。这也表明了在任意系统电压下，SVC-MERS都可以实现从0到额定电流的无功补偿。

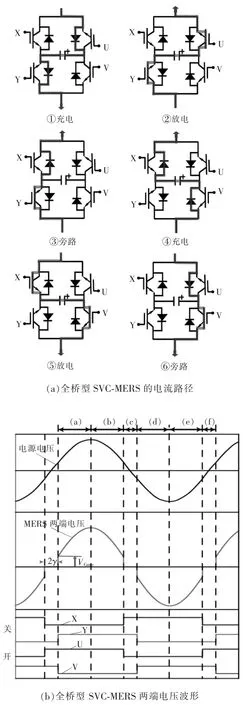
图3　全桥型SVC-MERS的电流路径及其两端电压波形Fig.3 Current paths of full-bridge SVC-MERS and voltage waveforms of its generalized form

2　三相对称系统中SVC-MERS的建模和注入谐波电流分析

在三相对称系统中SVC-MERS通常是由3个单相SVC-MERS接成三角形结构，从而能够从结构本身消除3次以及3倍频次谐波。以全桥型SVCMERS为例进行研究，其拓扑结构如图4所示。本文重点研究三相对称系统中SVC-MERS的注入线电流谐波特性，首先对SVC-MERS建立数学模型，进而推导出线电流的谐波含量计算方法。

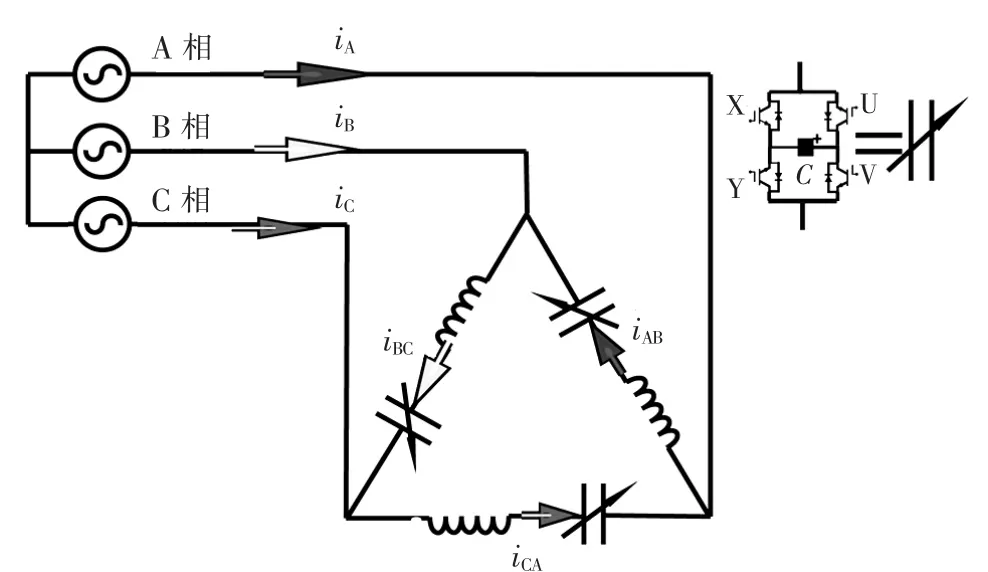
图4　三相对称系统中SVC-MERS结构Fig.4 Configuration of SVC-MERS in three-phase symmetrical power system

2.1三相对称系统中SVC-MERS数学模型

（1）在三相对称系统中，基于图3 SVC-MERS的基本工作状态，列电压电流方程。

连接在A相和B相之间的单相SVC-MERS的充电状态图3（a）和放电状态图3（b）可列微分方程分别为

妇幼保健机构往往对专业医疗队伍的培养充分重视,但在档案管理人员培养与管理方面重度不足,很多档案管理人员专业素养较为落后,没有相关培训进修机制,在当前档案管理工作中无法满足现实需求。另外,当前很多档案管理人员理论技术、管理经验较为缺乏,非常容易影响到档案收集管理工作完整性。

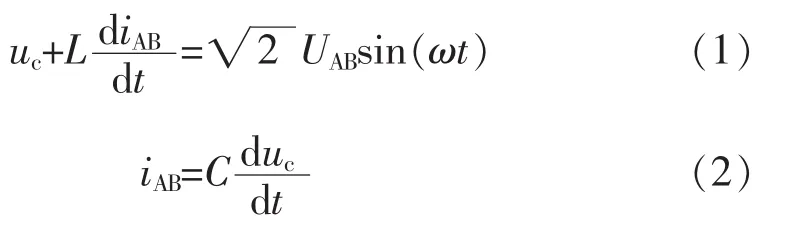
边界条件为：uc（γ/ω）=VCmin；uc（t=（π-γ）/ω）=VCmin。旁路状态图3（c）可列微分方程为

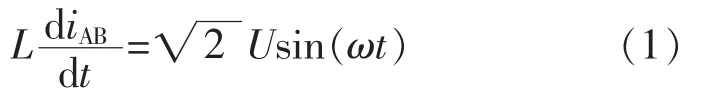
通过式（1）～式（3），可得相电流iAB表达式为

（2）根据三相对称系统中相电流之间的关系，可得出相电流iCA表达式为

其中：

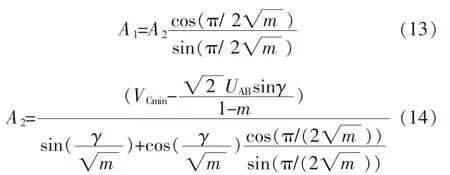
通过以上方程进一步可推出iA的表达式为

（3）通过式（15）可以得到iA线电流的谐波含量THD表达式，即

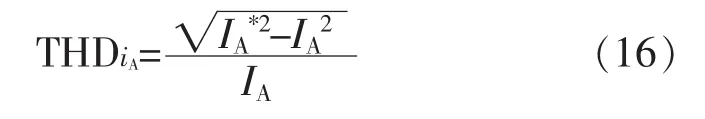
其中：

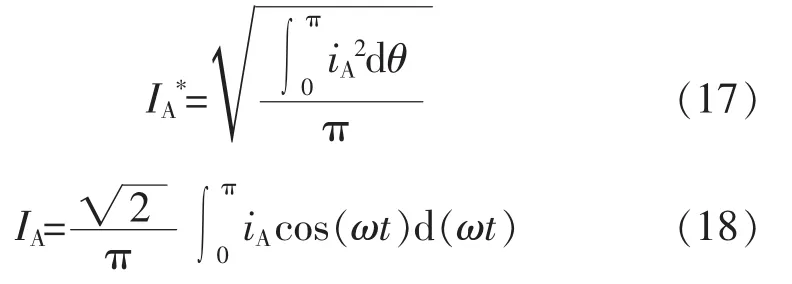
由以上推导过程可知，三相对称系统中SVCMERS的注入电流谐波含量取决于系统以及装置的硬件参数和控制参数2个方面的影响。在实际应用中，系统以及装置的硬件参数主要取决于系统所需要的无功补偿量等功能性要求。控制参数的合理设计可能有助于改善SVC-MERS的注入电流谐波特性。

2.2控制参数对SVC-MERS的注入线电流谐波含量的影响分析

本文建立了SVC-MERS的数学模型，对三相对称系统中SVC-MERS的注入线电流谐波含量进行了实例计算。在此基础上，详细分析了控制参数对注入系统线电流的谐波含量的影响。计算条件如下：三相对称系统的线电压有效值为380 V，电容C为118 μF，L为17 mH。根据第3.1节中推导出的公式，计算不同VCmin和γ的条件下注入系统线电流的谐波含量，计算结果分别如图5和图6所示。

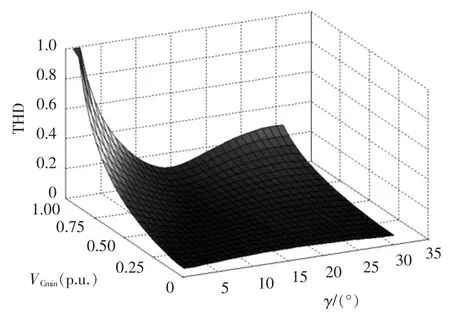
图5　THD随着γ和Vcmin变化情况Fig.5 Changes of THD with γ and Vcmin

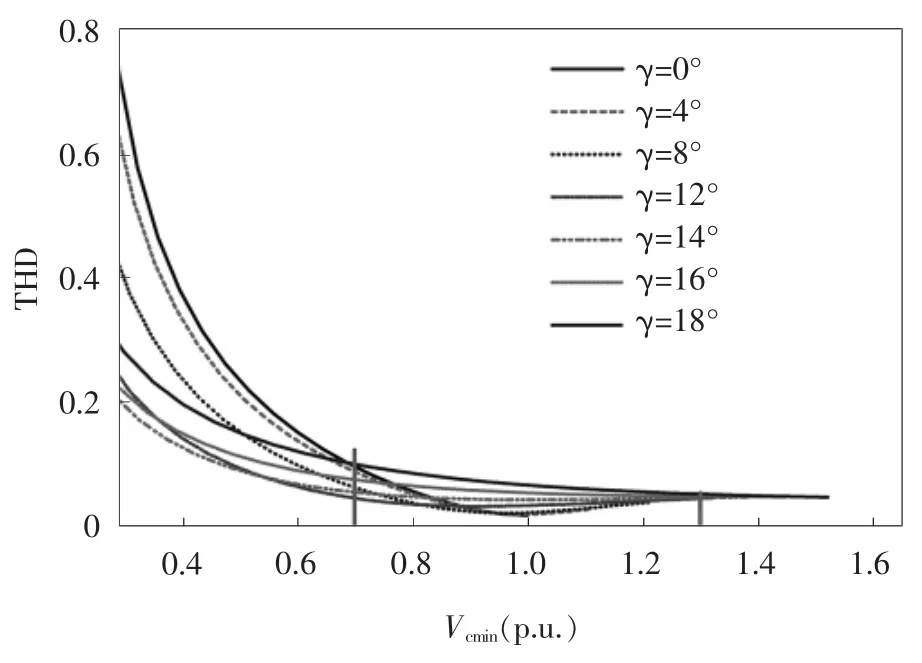
图6　THD随着γ和VCmin的变化情况Fig.6 Changes of THD with γ and VCmin

图5为SVC-MERS向系统注入线电流THD值随着控制参数的变化情况。由图可见，（1）三维图中存在一个凹沟；（2）γ在0°附近时，随着VCmin值的增大，其THD也逐渐变大，而且其值较大。从图5得到结论如下：（1）在不同的无功补偿量下存在最优的VCmin和γ的组合，使其谐波含量达到最小；（2）随着VCmin值的增大，无功补偿量逐渐减小，当无功补偿量很小，甚至接近于0时，三相对称系统中线电流的谐波含量THD值很高。

图6为SVC-MERS向系统注入线电流THD值随无功补偿量的变化情况，每条曲线代表了不同的γ值。由图可见，当无功补偿量一定时，γ值不同，三相对称系统中线电流中的谐波含量不同。进一步分析可得到结论如下：以固定电容的无功补偿量为基准，在三相对称系统中，当无功补偿量在1.3倍以上时，其THD值的变化与控制参数γ的关系不大；当无功补偿量在0.7～1.3倍之间时，THD值在控制参数γ=8°附近达到最好；当无功补偿量在0.7倍以下时，随着无功补偿量的减少，最佳γ略微出现了变化，但是基本稳定在γ=14°附近。

3　仿真与实验验证

本文采用PSIM软件对上述结论进行仿真验证。仿真条件为：SVC-MERS三角形连接，取三相对称电源的线电压U=380 V，C=118 μF，L=17.245 mH，即XL/XC≈0.2，f=50 Hz。在XMERS=XC时，其无功补偿量为20 kvar左右。仿真系统结构如图4所示。

3.1不同控制变量组合下的电压电流波形

假定所需无功补偿量为10 kvar，在控制变量VCmin和γ的不同组合条件下进行仿真，得到电压、线电流波形，并分析线电流的THD，结果如图7所示。

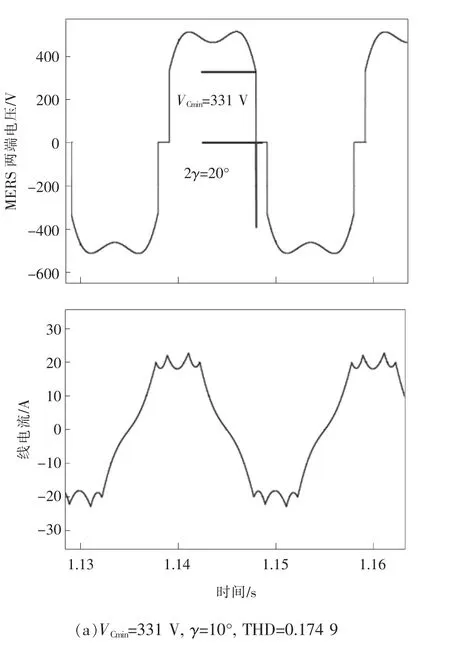
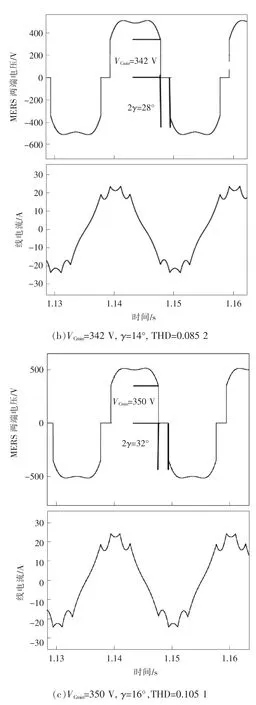
图7　不同VCmin和γ组合下的THD仿真结果Fig.7 Simulation results under different combination of VCminand γ

图（a）中，当VCmin=331 V，γ=10°时，线电流的THD为0.174 9；图（b）中，当VCmin=342 V，γ=14°时；线电流的THD=0.085 2；图（c）中，当VCmin=350 V，γ=16°时，线电流的THD为0.105 1。图7的仿真结果验证了2点结论：（1）不同的无功补偿量能够通过不同的VCmin和γ组合来实现；（2）不同的VCmin和γ组合，其THD值不同，即在无功补偿量一定时，存在最优的VCmin和γ组合使其谐波特性达到最优，并且无功补偿量小于0.7 p.u.时，控制参数γ的最优值在14°附近。

3.2控制参数γ、无功补偿量和线电流THD之间的量化关系

改变2个控制参数γ和VCmin的值，通过PISM软件进行多次仿真，得到SVC-MERS向系统注入线电流的谐波THD随控制参数的变化情况。其结果如图8所示。由图可见：（1）无功补偿量一定时，存在不同的VCmin和γ的组合；（2）以无功补偿量20 kvar为基准，当补偿量在1.3倍以上时，THD的值与控制参数γ的关系不大；当无功补偿量在0.7～1.3倍之间时，THD值在控制参数γ=8°附近的时候达到最好；当无功补偿量是0.7倍以下时，随着无功补偿量的减少，最佳的γ略微出现了变化，但是基本稳定在γ=14°的附近。

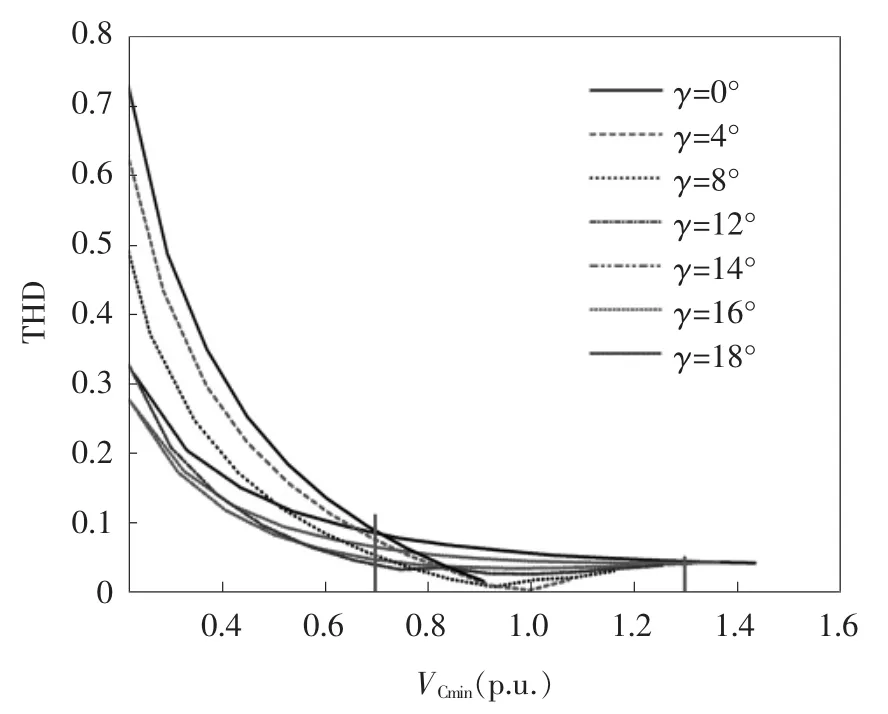
图8　THD随着γ和VCmin变化的仿真波形Fig.8 Simulation waveforms of THD changing with γ and VCmin

仿真结果和第3.2节中计算结果完全一致，这也验证了所提出的SVC-MERS数学模型以及线电流谐波含量计算方法的正确性。同时，所得到的结论可以对控制参数优化设计提供有效的指导。

3.3实验验证

实验具体参数如下：电感L=40 mH，电容C=50 μF，三相电源线电压U=50 V。验证所提出的SVCMERS注入线电流谐波计算方法以及所得到控制参数的优化设计方法的实验装置如图9所示。

图9　实验装置Fig.9 Test equipments

本文分别针对同一无功补偿量下不同控制参数组合下的电流实验波形进行了分析，其实验波形如图10所示。由图可见：（1）当无功补偿量大于1.3倍，即当VCmin=0 V，γ分别为10°、15°和20°时，其THD分别为0.090 3、0.086 5、0.089 9。对这组数据的分析很好地证明当无功补偿量为1.3倍以上，其线电流的THD值跟控制参数γ的关系不大。（2）当无功补偿量为0.6倍，VCmin=30 V，γ=8°时，THD值为0.070；当VCmin=35 V，γ=15°时，THD值为0.065；当VCmin=38 V，γ=17°时，THD值为0.144。对这组数据的分析，很好地证明了当无功补偿量是0.7倍以下时，随着无功补偿量的减少，最佳γ略微出现了变化，但是基本稳定在γ=14°的附近。

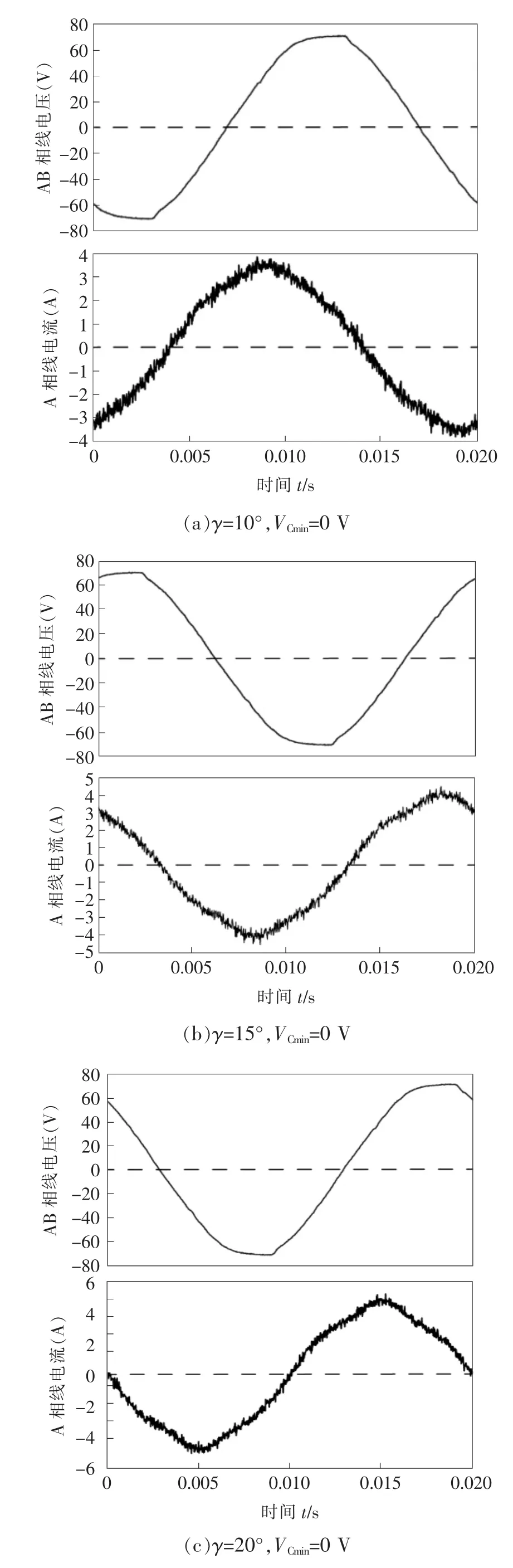
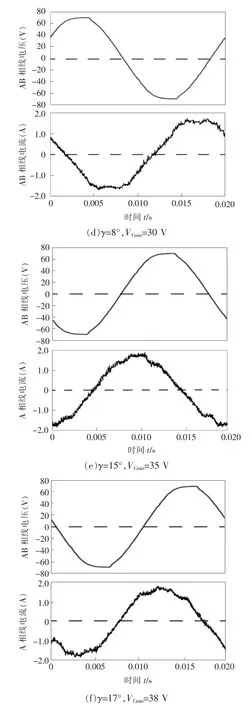
图10　线电流THD实验结果Fig.10 Test results of current THD

实验数据的分析结果表明所提出的SVC-MERS数学模型以及线电流谐波含量计算方法的正确性。同时，也很好地验证了关于控制参数优化设计的结论。

4　结论

本文对三相对称系统SVC-MERS进行数学建模，提出了SVC-MERS三角形连接时注入线电流谐波含量的计算方法。仿真和实验分别验证了所提出计算方法的正确性以及控制策略的可行性。

（1）不同的无功补偿量能够通过控制参数VCmin和γ不同组合来实现，同时其无功补偿量能够达到固定电容无功补偿的数倍，主要取决于SVC-MERS开关器件的耐压值和最大电流值。

（2）通过对控制参数γ的恰当的控制能够有效的降低线电流的谐波含量，改善其谐波特性，对SVCMERS在三相对称系统中的应用具有重要意义。

［1］刘万辉，程苗苗，冯凯.并联型HALF-MERS的性能分析和参数设计［C］.中国高校电力电子与电力传动学术年会，2013∶619-623. Liu Wanhui，Cheng Miaomiao，Feng Kai. The Performance of HALF-MERS and Parameter Design［C］. SPEED 2013. 2013∶619-623.（in Chinese）.

［2］蒋婷，江剑锋，曹中圣，等. STATCOM-感应电机风电场并网发电系统的仿真分析［J］.电源学报，2012，10（1）∶71-75. Jiang Ting，Jiang Jianfeng，Cao Zhongsheng，et al. Simulation analysis of STATCOM-induction machine wind farm grid connection power generation system［J］. Journal of Power Supply.2012，10（1）∶71-75.（in Chinese）.

［3］郜登科，杨喜军，雷淮刚，等.基于磁能恢复开关的单相串联补偿器的研究［J］.华东电力，2008，36（3）∶47-49. Hao Dengke，Yang Xijun，Lei Huaigang，et al. The research of single-phase series compensator based on the magnetic energy recovery switch［J］. East China Electric Power，2008，36（3）∶47-49（in Chinese）.

［4］Wiik J A，Wijaya F D，Shimada R. Characteristics of the Magnetic Energy Recovery Switch（MERS）as a Series FACTS Controller［J］. IEEE2009，24（2）∶828-836.

［5］Huzlik R，Vetiska V，Ondrusek C．Utilization of Magnetic Energy Recov ery Switch for Compensation of Reactive Power［C］．International Symposium on Power Electronics，Electrical Drives，Automation and Motion，2012：1290 -1294．

［6］Miaomiao Cheng，Isobe T，Kato S，et al. Applying MERS for induction motor driving［J］. JIPE，2012，37（12）∶139-145.

［7］Wiik J A，Wijaya F D，Shimada R. Characteristics of the magnetic energy recovery switch（MERS）as a series FACTS compensator［J］. IEEE Trans. On Power Dilivery，2009，23 （2）∶828-836.

［8］Miaomiao Cheng，Shiojima D，Isobe T，et al. Voltage Control of Induction Generator Powered Distributed System Using a New Reactive Power Compensator SVC-MERS ［C］. The 15th international Power Electronics and Motion Control Conference：EPE-PEMC 2012 ECCP Europr. 2012∶DS3b.7-1-DS3b.7-8.

［9］Wijaya F D，Isobe T，Usuki K，et al. A new induction generator voltage controller using controlled shunt capacitor，SVC magnetic energy recovery switch［J］. IEEJ Transactions on Industry Applications，2009，129（1）∶29-35.

［10］Shiojima D，Miaomiao Cheng，Isobe T，et al. Control and Design Principle of SVC-MERS-A New Reactive Power Compensator with Line Frequency Switching and Small Capacitor［C］. IEEE Energy Conversion Congress. 2012：2045-2052.

Analysis of Current Harmonics of SVC-MERS in Three-phase Symmetrical Power System

CHENG Miaomiao，BAO Yueyue，TU Chunming，ZHANG Zhongjie，LIU Zhiguo
（College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

Magnetic energy recovery switch（MERS）has been proposed as a new reactive power compensator. Compared with other reactive power compensation devices，it has many advantages，such as simple structure，easy to control and low loss. But MERS produce harmonic current in the process of reactive power compensation. Firstly，the configuration of MERS and the operating principles of MERS are described in the paper. Secondly，the electrical model of SVCMERS in three-phase symmetrical power system is described using analytical equations. Then，the effect of the control variables on current harmonics are analysed and the optimal combination of control variables are established. simulation and test are presented to verify the result.

three-phase symmetrical power system；shunt compensation；magnetic energy recovery switch（MERS）；current harmonic

程苗苗

2015-07-23

国家自然科学基金青年科学基金项目（51307048）；湖南省科技计划项目（2015WK3004）

程苗苗（1982-），女，博士，讲师，研究方向：飞轮电力储藏装置的开发以及应用、无功补偿、电机控制以及分散式电源系统的稳定性，E-mail：mmcheng_hnu@126.com。

包跃跃（1991-），男，通信作者，硕士研究生，研究方向：新型无功补偿装置的开发和应用，E -mail：yybao11011@163. com。

涂春鸣（1976-），男，博士，教授，博士生导师，研究方向：电力电子技术在电力系统中的应用，E-mail∶chunming_tu@263. net。

张忠杰（1989-），男，硕士研究生，研究方向：新型软开关功率变换器拓扑及其控制方法，E-mail：hncd_jie@163.com。

刘治国（1992-），男，硕士研究生，研究方向：软开关DC-DC变换器拓扑及其控制方法，E-mail：liu318429@163.com。