图像分块及惰性多示例学习鞋印图像识别
李大湘, 吴 倩, 李 娜, 刘 颖
(1. 西安邮电大学 通信与信息工程学院, 陕西 西安 710121; 2. 电子信息现场勘验应用技术公安部重点实验室, 陕西 西安 710121)
图像分块及惰性多示例学习鞋印图像识别
李大湘1,2, 吴倩1, 李娜1,2, 刘颖1,2
(1. 西安邮电大学 通信与信息工程学院, 陕西 西安 710121; 2. 电子信息现场勘验应用技术公安部重点实验室, 陕西 西安 710121)
摘要:结合图像分块与惰性多示例学习(MIL)给出一种鞋印识别新算法。将整个鞋印图像当作包,根据脚底生物特征比例,采用均匀网格分块的方法将鞋印图像分成15个子块,并提取每个子块的纹理与形状特征,当作包中的示例,将鞋印图像识别问题转化成MIL问题;然后,将推土机距离(EMD)应用到K最近邻 (KNN)算法中,得出一种惰性MIL新方法用于鞋印识别。在包含5种不同类型花纹的鞋印库中进行实验,识别正确率可达91.28%,较之基于欧氏距离的KNN算法,识别精度平均提高4.0%。
关键词:多示例学习;鞋印图像识别;纹理-形状特征
鞋印是犯罪现场最常见的痕迹物证[1]。随着刑侦科学的发展,从犯罪现场收集的鞋印图像越来越多。从大规模足迹库中找到与犯罪现场相匹配的鞋印,需要高效的图像自动识别技术[2]。已有鞋印识别算法[3-7],多是对整幅鞋印图像提取其全局纹理或形状特征,易受图像背景干扰,鞋印花纹在结构上的整体相似性不易到到反映,识别精度有限。
本文拟将图像当作包(bag),图像子块的视觉特征当作包中的示例(instance),基于图像分块与惰性多示例学习(multi-instancelearning,MIL)[8],给出一种鞋印识别新方法。
1基于“网格分块”的多示例建模
对鞋印图像进行高斯平滑与直方图均衡化预处理,采用“网格分块”的方法将鞋印图像划分成多个子块,并提取每个子块的纹理和形状等底层特征,作为包(图像)中的示例,将鞋印图像识别问题转化成标准的MIL问题。
1.1网格分块
鞋印图像可分为脚掌区、脚弓区和脚跟区三部分,并普遍遵循0.49∶0.20∶0.31的生物特征分割比例[2]。脚弓区通常残缺严重,纹理很少,为减少计算量,对其可不予考虑,而只把脚掌区和脚跟区采用均匀网格分块的方法划分为15个子块,如图1所示。

图1 鞋印图像网格分块
1.2特征提取
鞋印识别主要依赖图像的纹理与形状特征。
(1) 灰度共生纹理特征
分别针对距离差分值(1,0)、(1,1)、(0,1)与(-1,1),计算每个“子块”的灰度共生阵G及其能量E、熵H、对比度C和相关系数R,作为“子块”的纹理特征。
设某对灰度值(m,n)(1≤m,n≤L)对应的灰度共生阵元素为g(m,n),那么[9]

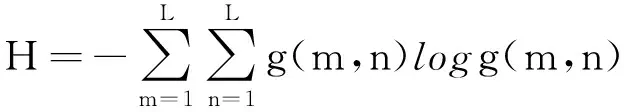


其中



(2) 不变矩形状特征
设“子块”f在(x,y)处的像素值为f(x,y),定义“子块”f的p+q阶原点矩Mp,q和p+q阶中心矩up,q分别为[10]


其中p和q为非负整数,H和W分别表示子块f的高和宽,(xc,yc)为“子块”f的重心,即

进而定义规范化中心矩

基于归一化的二阶和三阶中心矩,可构造7个不变矩[10]
ψ1=η2,0+η0,2,

ψ3=(η3,0-3η1,2)2+(η0,3-3η2,1)2,
ψ4=(η3,0+η1,2)2+(η0,3+η2,1)2,
ψ5=(η3,0-3η1,2)(η0,3+η1,2)[(η3,0+
η1,2)2-3(η0,3+η1,2)2]+
(3η2,1-η0,3)(η2,1+η0,3)[3(η3,0+
η1,2)2-(η0,3+η2,1)2],
ψ6=(η2,0-η0,2)[(η3,0+η1,2)2-
(η0,3+η2,1)2]+4η1,1(η3,0+
η1,2)(η0,3+η2,1),
ψ7=(3η2,1-η0,3)(η3,0+η1,2)[(η3,0+
η1,2)2-3(η0,3+η2,1)2]+
(3η1,2-η3,0)(η2,1+η0,3)[3(η3,0+
η1,2)2-(η0,3+η2,1)2]。
通过分块与特征提取,可将任一鞋印图像转化成多示例包
B={Xt∈23: t=1,2,…,15}。
2惰性MIL鞋印识别算法
记由N个多示例包(鞋印图像)组成的训练集
D={(Bi,yi):i=1,2,…,N},
其中
Bi={Xi,j: j=1,2,…,15}(i=1,2,…,N)
表示由15个示例Xi,j∈23(j=1,2,…,15)组成的第i个多示例包,yi为Bi的类别标号。
2.1惰性MIL算法
为了用K最近邻(K-nearestneighbor,KNN))惰性算法进行鞋印图像识别,采用推土机距离(EarthMoversDistance,EMD)[11]来度量多示例包之间的相似度。
分别记第r幅和第s幅鞋印图像对应的多示例包为
Br={Xr,j: j=1,2,…,15},
Bs={Xs,k: k=1,2,…,15},
两者中的示例Xr,j与Xs,k之间的欧氏距离
cj,k=‖Xr,j-Xs,k‖,
则求解多标例包Br与Bs之间的EMD距离,可转化成线性优化问题
即寻找最优流量
F=(aj,k)15×15,
以使其目标函数达到最小值。
确定F之后,定义Br与Bs之间的EMD距离为

2.2鞋印识别算法
惰性MIL鞋印识别算法可描述如下。
输入带有类别标号的鞋印图像训练集D,待识别的图像I,以及KNN算法中的K值。
输出图像I的识别结果。
步骤1对D中的每幅图像进行分块与特征提取,将其构造成多示例包
D={(Bi,yi): i=1,2,…,N}。
步骤2对待识别图像I进行分块与特征提取,将其构造成多示例包
I={Xj: j=1,2,…,15}。
步骤3计算多示例包I与D中每个包之间的EMD距离,选择I的K近邻。
步骤4统计I的K近邻类别标号,将I归入标号最多的类别。
3实验结果
选取150幅鞋印图像作为训练测试集,这些图像分为折波型、交织型、线条型、边块型与圆点型(其类型号依次记为1至5),每类30幅。对所有图像进行方向校正、二值化及尺度归一化处理,部分样图如图2所示。

图2 训练测试集图例
从每类图像中随机选取10幅组成训练集,其余20幅组成测试集,设置KNN算法的参数K为10。经10次随机实验,得平均识别准确率的混淆矩阵

其中对角线上的数据表示每类的识别准确率,其余数据表示相应的错误率。
对训练测试集中所有鞋印图像提取其全局“灰度共生纹理”与“不变矩形状特征”,将新算法与基于欧氏距离的KNN算法[12]进行对比。
从每类图像中随机选取10幅组成训练集,其余20幅组成测试集。分别设置KNN算法的参数K为5或10。经10次随机实验,所得平均查全率与查准率如表1和表2所示,可见,在不同参数设置下,新方法均优于基于欧氏距离的KNN算法。

表1 识别精度对比(K=5)

表2 识别精度对比(K=10)
在鞋印图像识别时,依据多个相关子块的共同作用,可以获得更佳识别效果。EMD距离能自动在两个图像的不同子块间完成最佳匹配,更好地反映了图像间的整体相似度,对图像分块精度不太敏感,这正是新算法精度得以提升的原因所在。
4结语
针对鞋印图像识别问题,基于图像分块与惰性MIL算法,给出一种鞋印识别新方法,对比实验结果表明,该鞋印识别方法简单有效,且识别精度高于基于欧氏距离的KNN算法。
参考文献
[1]高毅, 陈青, 叶泸键,等. 足迹边缘弧度变化区分足别的量化研究[J]. 中国人民公安大学学报:自然科学版, 2013, 77(3): 6-10.
[2]刘家浩. 鞋印图像识别算法的研究及系统实现[D]. 大连:大连海事大学, 2012:3-28.
[3]SUHJ,CROOKESD,BOURIDANEA.Thresholdingofnoisyshoeprintimagesbasedonpixelcontext[J].PatternRecognitionLetters, 2007, 28(1): 301-307.
[4]马臣. 基于LBP与形状上下文的足迹比对算法研究[D]. 大连:大连海事大学, 2014:5-24.
[5]CHAZALP,FLYNNJ,REILLYRB.AutomatedprocessingofshoeprintimagesbasedontheFouriertransformforuseinforensicscience[J].IEEETransactionsonPatternAnalysisandMachineIntelligence. 2005, 27(3): 341-350.
[6]KHANMA,TIDKESM.AutomatedProcessingofShoeprintImagesforUseinForensicScience[J].InternationalJournalofAdvancedResearchinComputerandCommunicationEngineering, 2013, 2(11): 4292-4294.
[7]NIBOUCHEO,BOURIDANEA,CROOKESD.RotationinvariantmatchingofpartialShoeprints[C]//13thInternationalMachineVisionandImageProcessingConference.IrelandDublin:IEEE, 2009: 94-98.
[8]李大湘,赵小强,刘颖,等. 融合SIFT与MIL的红外人脸识别方法[J]. 西安邮电学院学报,2012,17(4):15-20.
[9]贾世杰,石薇,曾洁,等. 基于纹理特征的鞋底花纹识别分类[J]. 大连交通大学学报, 2008,29(1):59-63.
[10]ALGARNIG,HAMIANEM.Anoveltechniqueforautomaticshoeprintimageretrieval[J].ForensicScienceInternational, 2008, 181(10): 10-14.
[11] 李大湘, 彭进业, 贺静芳. 基于EMD-CkNN多示例学习算法的图像分类[J]. 光电子·激光, 2010, 21(2): 302-306.
[12] 刘颖,黄源,高梓铭.刑侦图像检索中的特征提取及相似性度量[J].西安邮电大学学报, 2014, 19(6): 11-16.
[责任编辑:瑞金]
Shoeprintimagerecognitionalgorithmbasedonimageblockandlazymulti-instancelearning
LIDaxiang1,2,WUQian1,LINa1,2,LIUYing1,2
(1.SchoolofCommunicationandInformationEngineering,Xi’anUniversityofPostsandTelecommunications,Xi’an710121,China;2.MinistryofPublicSecurityKeyLaboratoryofElectronicInformationApplicationTechnologyforSceneInvestigation,Xi’an710121,China)
Abstract:A novel shoeprint recognition algorithm is proposed based on image block and lazy multi-instance learning (MIL). Firstly, the algorithm regards every shoeprint image as a bag. Then according to the proportion of foot biometrics, a uniform grid partitioning method is used to divide shoeprint image into 15 sub-blocks, and the texture and shape features of each block are extracted. Therefore the shoeprint image recognition problem is transform into a MIL problem. Secondly, the earth mover’s distance (EMD) is introduced into the traditional k-nearest neighbour (KNN) method to improve the accuracy of image similarity measure, and a new lazy MIL algorithm is designed for shoe prints recognition. Experimental results on shoeprint images datasets where contains five different types of shoeprint pattern indicate that the recognition accuracy of the new method can reach 91.28%, and that compared with Euclidean distance based KNN algorithm, its average recognition accuracy is improved by 4%.
Keywords:multi-instance learning (MIL), shoeprint image recognition, texture-shape features
doi:10.13682/j.issn.2095-6533.2016.01.011
收稿日期:2015-09-08
基金项目:公安部科技强警基础工作专项基金资助项目(2014GABJC022);陕西省自然科学基金资助项目(2013JM8031,2015KW-014);陕西省教育厅科学研究计划资助项目(15JK1660, 15JK1661);中国博士后科研基金资助项目(2013M542386).
作者简介:李大湘 (1974-),男,博士,副教授,从事刑侦图像分析研究。E-mail: www_ldx@163.com 吴倩 (1991-),女,硕士研究生,研究方向为信号与信息处理。E-mail:35108809@qq.com
中图分类号:TP391
文献标识码:A
文章编号:2095-6533(2016)01-0059-04

