基于线列阵组合圆周阵声源的远场指向性分析
法 林, 韩永兰, 王 军, 赵 洁, 刘世朋
(西安邮电大学 电子工程学院,陕西 西安 710121)
基于线列阵组合圆周阵声源的远场指向性分析
法林, 韩永兰, 王军, 赵洁, 刘世朋
(西安邮电大学 电子工程学院,陕西 西安 710121)
摘要:利用Bridge乘积定理推导出线列阵组合圆周阵声源的远场指向性函数,采用数值方法对声源的指向性进行仿真分析,并与线列阵及点源均匀圆周阵声源的远场指向性进行比较。结果表明,在相同指向性要求下,线列阵组合圆周阵声源比线列阵及点源均匀圆周阵所构成声源的指向性都好,更有利于声源的小型化。
关键词:线列阵组合圆周阵声源;线列阵;点源均匀圆周阵;指向性
压电换能器[1-2]是一种进行电—声和声—电能量转换的器件,在医疗[3]、军事[4]、地震勘探和声波测井[5]等领域已得到广泛应用。实际应用要求压电换能器逐步向着高灵敏度、强指向性、大功率等方向发展,在衡量声波辐射定向效果方面,指向性是评价系统性能的重要指标之一[6]。
换能器组合阵列形式的声源是声波定向的关键技术之一[7]。利用圆形活塞组成的圆周阵[8]和利用单个换能器组成的线阵组合平面阵[9]都具有较好的指向性,但在高声频下不能有效地抑制旁瓣和栅瓣幅值,不利于强指向性的实现,也不利于装置的小型化。本文基于二维阵列形式对指向性的影响规律[10],设计一种新型的三维线列阵组合圆周阵声源。结合线列阵及点源均匀圆周阵较好指向性特点,利用复合系统的指向性理论,在远场条件下推导出此声源的指向性函数,并对其所涉及到的结构尺寸对指向性的影响进行研究和分析。
1线列阵组合圆周阵声源远场指向性函数
1.1组合声源指向性函数
组合声源是按照一定的方式将单一声源组合在一起形成声源阵列,从而达到改善声源辐射声场的指向性性能。通常采用Bridge乘积定理[9]对组合声源求指向性。设一级子阵的指向性为D1(α,θ),二级子阵的指向性为D2(α,θ),以此类推,n级子阵的指向性为Dn(α,θ),由n个子阵所构成的组合阵声源指向性函数[8]为D(α,θ)=D1(α,θ)D2(α,θ)…Dn-1(α,θ)Dn(α,θ),
(1)
式中α为声线在xoy平面上投影与x轴间的夹角,θ为声线与z轴正方向间的夹角。
1.2线列阵组合圆周阵指向性函数
线列阵组合圆周阵如图1所示。它由N个线阵列均匀排列在半径为a的弧面构成。其中由M个阵元沿z轴排列组成线列阵一级子阵,其阵元间距记为l,e为声线方向的单位向量。xOy平面上均匀分布的点构成点源均匀圆周阵二级子阵。根据Bridge定理,此阵列指向性函数为线列阵指向性函数与点源均匀圆周阵指向性函数的乘积。

图1 线列阵组合圆周阵
一级子阵的线列阵[9]如图2所示,它对应的指向性函数为
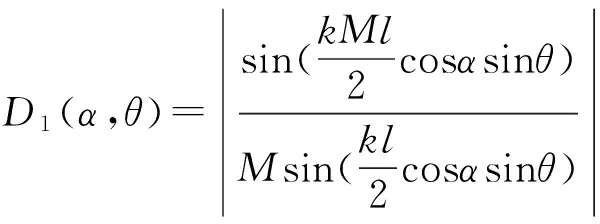
(2)
其中M为线阵阵元的个数,l为阵元之间的间距,k为波数。
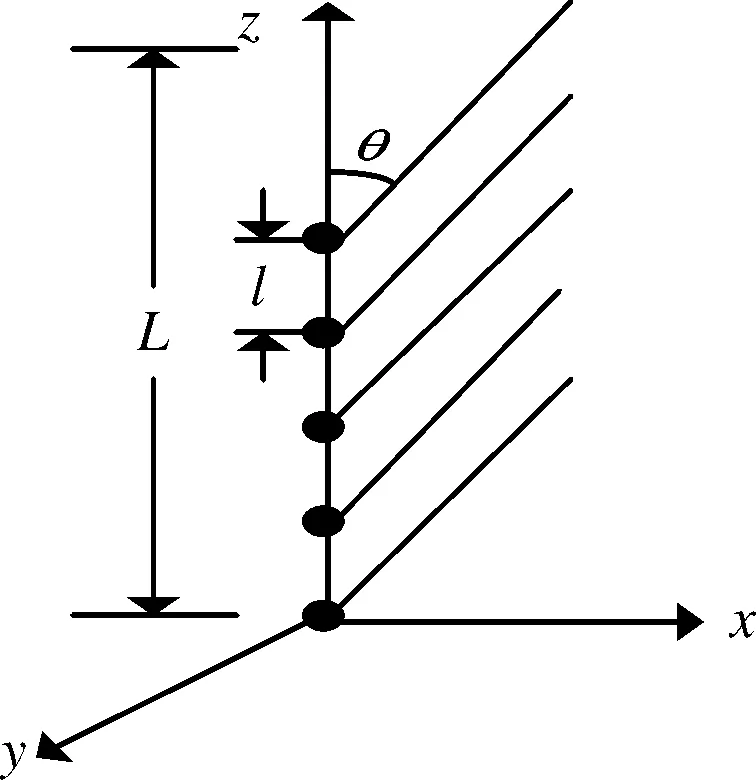
图2 线列阵结构
二级子阵的点源均匀圆周阵如图3所示。

图3 点源均匀圆周阵结构
在xOy平面上,设有N个声源均匀排列在以圆心为坐标原点半径为a的圆周上。第i个阵元坐标记为(xi,yi),方位角记为αi,矢径记为ri,e为声线方向的单位向量,m为各阵元径相位或延时补偿后主极大方向上的单位向量,则点源均匀圆周阵的指向性函数[8]可表示为

(3)
结合式(2)和式(3)可得线列阵组合圆周阵指向性函数
D(α,θ)=D1(α,θ)D2(α,θ)=

(4)
2线列阵组合圆周阵声源远场指向性仿真及分析
2.1圆周阵换能器数目远场指向性的影响
取定线列阵上换能器个数M=8,l=0.008 m,波数k=300,a=0.02 m,分别取N=4、6、8、10,得到如图3所示一组声源远场指向性仿真图(各图右下角所附为其中心点附近的局部放大图,下文与此相同)。

图3线列阵组合圆周阵声源远场指向性随N变化时的仿真结果及局部放大图
从图3可看出对此声源,当只改变圆周阵中换能器的个数N时,随着N的增大,其主瓣宽度基本没有变化,但从局部放大图可明显看到旁瓣、栅瓣数量增加,并且旁瓣、栅瓣的幅值大小随N的增大而减小。说明增大N时可增加此声源旁瓣、栅瓣个数,同时也可抑制其幅值,从而可有效提高其远场指向性能。为了获取体积小、性能优良的声源,此处折中取圆周阵上换能器的个数N=8,以便对其他参数进行研究与分析。
2.2圆周阵半径对远场指向性的影响设参数
M=8,N=8,l=0.008 m,k=300,
分别取a=0.02 m,0.04 m,0.06 m及0.08 m得到如图4所示的远场指向性仿真结果图。
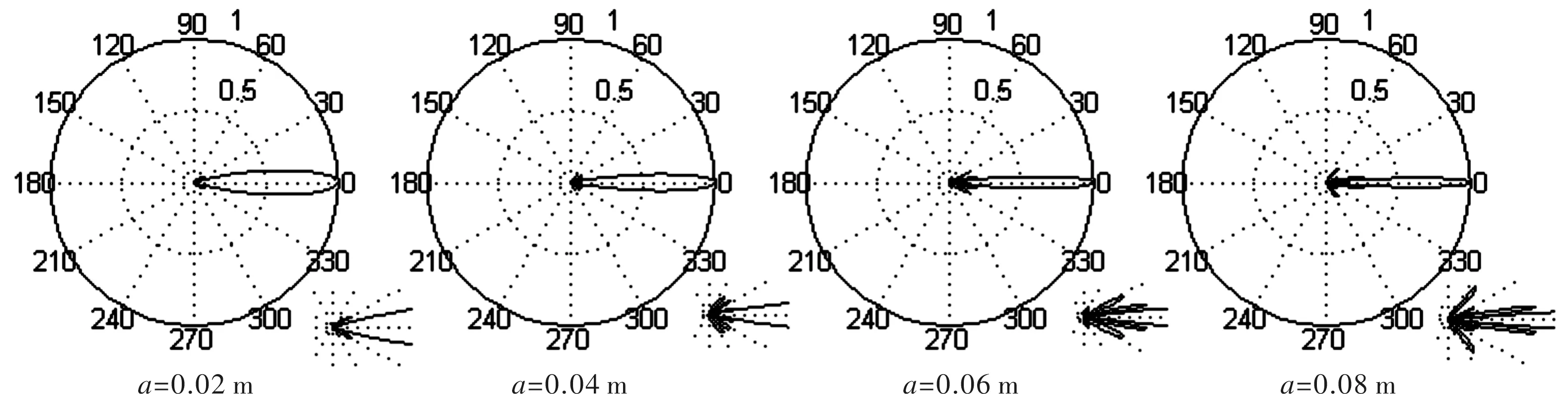
图4 线列阵组合圆周阵声源远场指向性随a变化时的仿真结果及局部放大图
从图4可看出,随着半径a增大,其主瓣宽度越来越窄(即主瓣越来越尖锐),同时从局部放大图可明显的看出旁瓣和栅瓣的数量逐渐增多,幅值也不断增大。说明增大半径a可以明显提高此声源的远场指向性,但并不是a越大越好,因为当a变大时其对旁瓣和栅瓣幅值抑制作用会减弱。因此,为得到良好的指向性,选取此声源半径a=0.04 m。
2.3线列阵换能器数目对远场指向性的影响
设定
N=8,l=0.008 m,k=300,a=0.04 m,
分别取M值为4、8、12、16得到如图5所示远场指向性仿真结果图。

图5 线列阵组合圆周阵声源远场指向性随M变化时的仿真结果及局部放大图
从图5及其局部放大图可看出,随着线列阵上换能器个数M增加,其主瓣宽度变窄,同时旁瓣和栅瓣数量增多且幅值得到抑制。这说明增加M可有效提高此声源远场指向性,但为得到小体积、指向性优良的声源,折中选取M=12。
2.4 线列阵相邻换能器间的距离对远场指向性的影响
选取相关参数M=12,N=8,k=300,a=0.04 m,l分别取值0.004 m、0.008 m、0.012 m及0.016 m得到如图6所示远场指向性仿真结果图。

图6线列阵组合圆周阵声源远场指向性随l变化时的仿真结果及局部放大图
从图6可观察到,随着l增大,主瓣宽度逐渐变窄,旁瓣和栅瓣的数量不断增加,同时旁瓣和栅瓣幅值得到抑制。这些都有效提高此声源远场指向性,但为获取小体积、指向性优良的声源,选取参数M=12,N=8,k=300,a=0.04 m,l=0.012 m作为优化线阵列组合圆周阵声源的结构参数值。
3各声源远场指向性比较
分别将所设计声源与点源均匀圆周阵和线列阵声源进行指向性对比分析。对于点源均匀圆周阵所用到的参数为N=8、a=0.04 m;对于线列阵所用到的参数为M=12,l=0.012;对于线列阵组合圆周阵所用到的参数为上述的优化结构参数值。它们在对应结构下远场指向性随波数k变化的仿真结果分别如图7、图8和图9所示。
从图7、图8和图9可看出,从低声频到高声频(即k从100到700)变化时,在对应相同结构参数下,线列阵组合圆周阵声源相比于点源均匀圆周阵和线列阵声源,远场指向性主瓣宽度得到进一步窄化,并且高声频时旁瓣和栅瓣幅值得到有效抑制。说明线列阵组合圆周阵声源无论是在低声频还是高声频都具有优良远场指向性。因此在获取相同指向性性能下,更有利于声源的小型化。

图7 点源均匀圆周阵随波数k变化的远场指向性仿真结果

图8 线列阵随波数k变化的远场指向性仿真结果

图9 线列阵组合圆周阵随波数k变化的远场指向性仿真结果
4结束语
通过Bridge乘积定理推导出线列阵组合圆周阵声源所对应的指向性函数,并对结构参数进行指向性性能仿真与分析比较。结果表明,在优化结构尺寸下,所提出的声源指向性比分别利用点源均匀圆周阵及线列阵所构成声源的指向性都好,更有利于声源的小型化。
参考文献
[1]杨庆庆, 李全禄, 吴晶, 等. 无铅压电超声换能器材料及其应用[J].西安邮电学院学报, 2011, 16(S2): 1-3.
[2]法林,郑雅娟,田勇.几个基本力学网络的机—电类比分析[J].西安邮电学院学报, 2011, 16(4): 66-70.
[3]王华.激光光束检测圆对称超声换能器焦点声压的可行性[J].激光杂志,2014,35(9):103-105.DOI:10.14016/j.cnki.jgzz.2014.09.103.
[4]聂正南,翟晓军.声频定向驱散系统指向性仿真研究[J].计算机仿真,2013,30(1):36-39.
[5]法林,王蕾,郑雅娟,等.声学在石油测井和地球物理勘探中应用的研究新进展[J].石油仪器,2012,26(2):1-6.
[6]张明,宋蕊,江雨春,等.典型活塞换能器声场分布及其指向性[J].解放军理工大学学报.2014,15(5):412-421.DOI:10.7666/j.issn.1009-3443.201306006.
[7]熊斌辉.声波定向随钻对接钻井技术及其运用[J].海洋石油,2014,34(1):86-91.DOI:10.3969/j.issn.1008-2336.2014.01.086
[8]张勋,许文海,董丽丽,等.圆形活塞圆周阵组合声源的远场指向性[J].大连海事大学学报,2008,34(1):91-94.
[9]巩建辉,严碧歌.线阵组合平面阵的指向性研究[J].南阳师范学院学报,2011,10(6):21-24.
[10]杨天文,陈 敏,黄大贵,等.换能器阵列形式对指向性的影响压[J].压电与声光,2014,36(1):93-99.DOI:10.3969/j.issn.1004-2474.2014.01.023.
[责任编辑:祝剑]
Directivity analysis on far-field sound source based on line array combination circumferential array sound source
FA Lin,HAN Yonglan,WANG Jun,ZHAO Jie,LIU Shipeng
(School of Electronics Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)
Abstract:The far field directivity function of line array combination circular array source is derived by applying Bridge product theorem. Numerical method is used for the simulation analysis of the sound source directivity. The result is compared with that of the far sound field directivity of linear array and uniform circumferential array of point source. Results show that under the same directional requirement, the directivity of line array combination circular array source is better than that of linear array and uniform circumferential array of point source. This is more useful for the miniaturization of the sound source.
Keywords:line array combination circumferential array sound source,line array,uniform circumferential array of point source,directivity
doi:10.13682/j.issn.2095-6533.2016.01.012
收稿日期:2015-04-14
基金项目:国家自然科学基金资助项目( 40974078)
作者简介:法林(1955-),男,教授,从事声学地球物理探测及信号处理研究。E-mail:fa_yy@yahoo.com.cn. 韩永兰(1989-),女,硕士研究生,研究方向为声光电交叉学科理论及其应用。E-mail:351198882@qq.com.
中图分类号:O424
文献标识码:A
文章编号:2095-6533(2016)01-0063-05

