平面阵指向性指数估算的改进

诸洁琪，申屠铠宇，陈伏虎

(杭州应用声学研究所，浙江杭州310012)

0 引 言

平面阵声呐具有广泛的用途，特别是潜艇舷侧等可布阵面积较大的区域，采用平面阵方式布阵可充分利用空间，提高声呐探测能力，如美国海狼级核潜艇、弗吉尼亚级核潜艇舷侧阵均采用了平面布阵方式。

声基阵的阵增益是声呐方程中计算作用距离的重要参数，定义为接收的信号增益与噪声增益比值的对数。由于其依赖于信号与遍布基阵的噪声的相干性，所以计算其具体的值并不容易。当信号为平面波且相干，噪声为各向同性且不相干时，声基阵的阵增益等于其指向性指数，即从各向同性噪声场中提取平面波信号的能力。估算声呐作用距离时，一般用指向性指数代替阵增益计算，并采用通用的估算公式估计声基阵的指向性指数。但实际计算时发现，常用的平面阵指向性指数估算结果[1]往往与实际计算值有较大偏差，导致估算声呐性能产生偏差。国外许多书籍对平面阵指向性指数的也存在多种不同估算公式，或未给出详细论证过程，或未给出简洁的估算表达式，且估算偏差各有不同[1-6]。因此本文对平面阵的指向性指数估算公式进行推导和改进，给出了清晰了理论支撑和简洁的表达式，使估算精度相比其他估算公式具备更小的偏差和更大的应用范围。

1 估算公式推导

接收阵的指向性因数Rθ是在各向同性噪声场无指向性接收器输出，与具有同样灵敏度的指向性阵输出的比值：

式中：D表示基阵的指向性函数；θ、φ分别为俯仰角和方位角。估算声呐作用距离的指向性指数与指向性因数关系为DI= 1 0lg (Rθ)，平面阵指向性指数常采用以下公式估算[1]：

式中：m、n分别为平面阵的水平方向和垂直方向阵元数，阵元间距为λ/ 2 ，N为声波波长。式(2)为背部无遮挡情况下平面阵的估算公式，实际应用中，《实用声呐工程》对背部存在遮挡，任意工作频率下的平面阵指向性指数估算公式[1]为

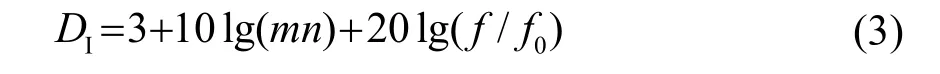
式中： f0表示阵元间距对应的最高工作频率，f＜f0。式(3)中默认平面阵水平、垂直阵元间距相等，实际中考虑到海洋声传播特性，声入射角一般为小掠射角，即使通过深海海底反射的入射信号的垂直俯仰角度也一般不超过−60°，因此实际上平面阵垂直俯仰角度无需到±90°，因而垂直方向阵元间距往往可略大于水平阵元间距。

在水平、垂直阵元间距不同，且满足小于λ/ 2 的情况下，式(3)可用以下公式表达：

式中：L、H分别为平面阵的长和宽。

实际应用时，发现式(4)的估算结果往往与实际计算值相差1 dB以上。因此，本文对平面阵的指向性指数估算公式进行推导，并建立更为准确的估算公式。

根据乘法定理，均匀分布的平面阵指向性函数可看成两条直线阵指向性函数的乘积。为方便计算，现建立如图1所示坐标系。

图1 指向性函数计算坐标系Fig.1 The coordinate system for directivity function calculation

令平面阵位于xOy平面内，y轴方向和z轴方向阵长分别为 L、H，d1、d2分别为 y轴方向和 z轴方向阵元间距，m、n为y轴方向和z轴方向阵元数。根据乘积定理[4]，平面阵指向性函数D (θ, φ) 为线阵指向性函数之积：

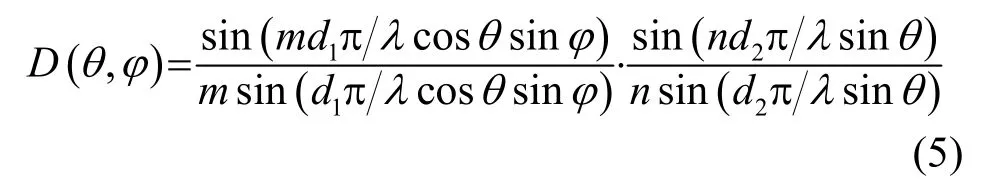
在实际的声呐设计中，离散线阵的指向性函数可以用式(6)的连续阵的指向性函数代替，两者造成的差异一般不大[6]。

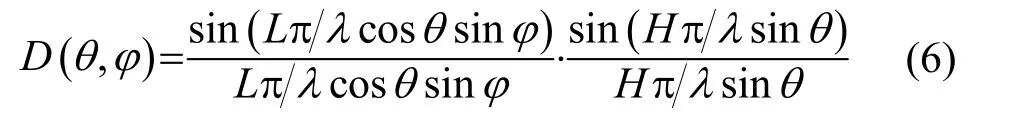
根据指向性因数计算公式，当平面阵背部遮挡时，指向性因数可转化为

将B的近似值代入式(7)，可得指向性因数近似公式为

式中：S为平面阵有效面积。则指向性指数的近似公式为

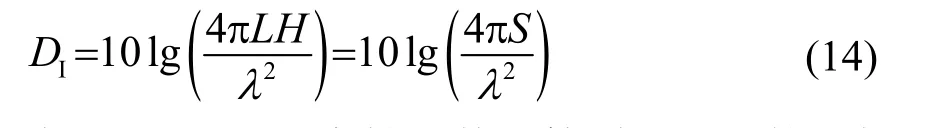
式(14)即根据指向性指数计算原理推导的近似计算公式，其推导过程是基于平面阵的长和宽远大于信号波长。主波束宽度较小的基础上得到的。因此当平面阵长或宽与信号波长相差较小时，该近似公式计算值与实际相差较大。

该公式计算值比式(4)大近2 dB，可见两者之间存在很大差别，必有其中一个近似公式与实际指向性指数的误差较大。因此，需通过仿真来分析其具体适用情况。

2 仿真分析

2.1 准确性分析

为验证指向性指数估算公式的准确性，本文对平面阵指向性指数进行仿真计算，并与估算公式比较，计算其误差。指向性指数真值根据式(1)积分公式对指向性函数D(θ, φ)进行积分计算，得到指向性因数Rθ后，根据DI= 1 0lg (Rθ)算得。

令平面阵的长、宽分别为8 m和4 m，阵元间距为0.1 m，则最高工作频率为7.5 kHz。该阵在6 kHz处的水平及垂直波束图如图2所示，其中水平和垂直方向波束宽度分别为 1.57°、2.96°，旁瓣级均为−13.3 dB。通过积分计算得指向性指数真值为38.04 dB，通过式(4)和式(14)的估算公式得到指向性指数估算值分别为36.11 dB和38.08 dB，由此可见，式(4)对平面阵指向性指数的估计偏差近2 dB，而采用式(14)进行估计的偏差小于0.1 dB，可认为式(14)的指向性指数估算结果基本与实际值相等。

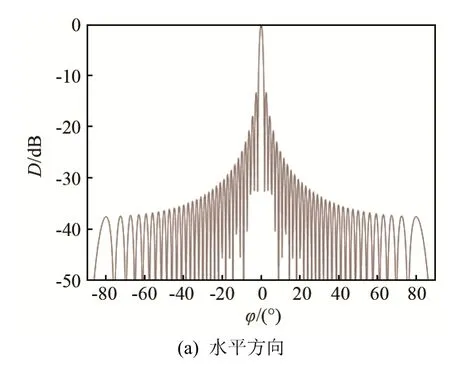
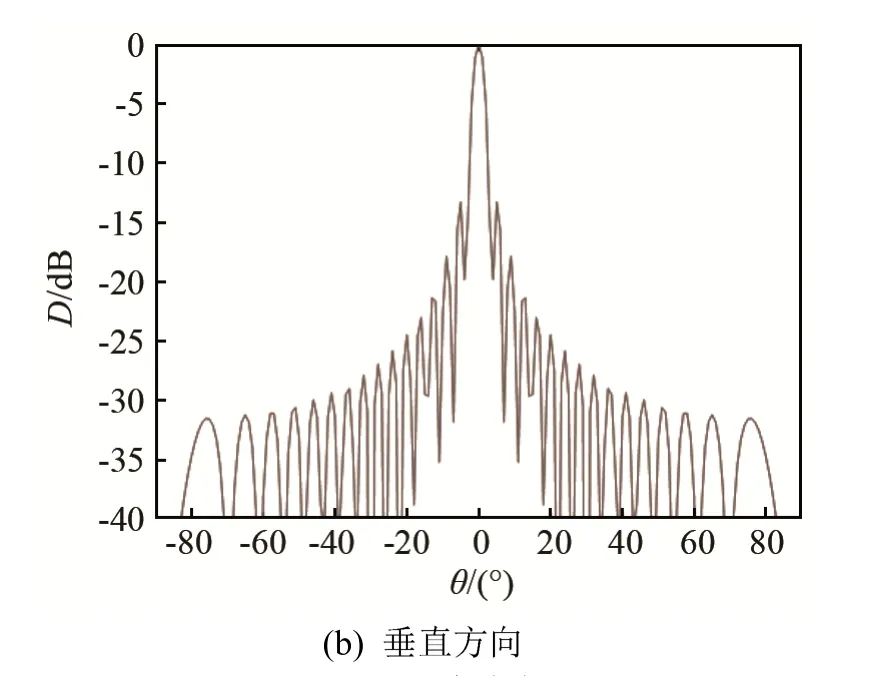
图2 平面阵波束图Fig.2 Beam pattern of planar array

2.2 阵元间距影响分析

式(14)的指向性指数估算公式虽与阵元间距无关，但其前提假设是离散平面阵指向性函数式(5)近似为连续平面阵指向性函数式(6)。这就要求阵元间距不能过大，否则会对估算准确度产生一定的影响。

实际上阵元间距大小对指向性指数影响是相对于信号波长而言的，即影响参数为阵元间距相对信号波长的比值。为验证阵元间距波长比对指向性指数估算准确度的影响，本文对不同频率(波长)下的平面阵指向性指数估算误差进行比较分析。

令平面阵的长、宽分别为8 m和4 m，阵元间距为0.1 m，信号频率为0.5～7.5 kHz，水中参考声速取1 500 m·s-1，则阵元间距波长比为0.03～0.5，此时该阵的波束宽度如图3所示，水平波束宽度为1.2°～19.1°，垂直波束宽度为 2.3°～38.7°。

图3 平面阵波束宽度Fig.3 Beamwidth of planar array

指向性指数计算值和估算值变化情况如图4所示，图中方法一估算值是采用式(4)的估算结果，方法二估算值是采用式(14)的估算结果。分析表明，在不同阵元间距波长比(不同频率)下，虽然已无法满足接近连续平面阵条件，但采用式(14)的估算结果依然与实际值基本相等，估算效果优于式(4)。

图4 不同方法指向性指数分析Fig.4 Directivity index analyses of different methods

2.3 阵孔径影响分析

本文指向性指数估算公式的第二个假设是阵的水平、垂直孔径远大于信号波长，使阵具有较小的波束宽度，波束图能量主要集中在主极大方向附近。为验证平面阵孔径对指向性指数估算准确度的影响，特别是阵孔径与波长接近时估算的准确度情况，本文对不同基阵孔径下的指向性指数估算误差进行了比较分析。在2.2节不同频率下指向性指数的分析中，信号频率低至 500 Hz时，波长与平面阵长、宽比值分别为0.375、0.75，水平、垂直波束宽度分别为19.1°、38.7°，此时式(14)对指向性指数的估计依然具有较高的准确性。

在实际使用时，如潜艇舷侧布阵，平面阵的长度远大于宽度，一般长度可达到几十米，而宽度在1～3 m左右，此时长度远大于波长，而宽度可能与波长接近甚至小于波长，本文对该情况下，不同平面阵宽度时指向性指数估算误差进行比较分析，验证阵孔径对估算准确度的影响。

设平面阵长为8 m，阵元间距为0.1 m，信号频率为 6 kHz，阵宽度为 0.2～4 m，则波长与宽度比值为0.0625～1.25，此时平面阵垂直波束宽度为3.0°～77.2°，如图5所示。指向性指数计算值和估算值变化情况如图6所示，其中方法一估算值即采用式(4)的估算结果，方法二估算值即采用式(14)的估算结果。分析表明，在波长宽度比小于0.42时，采用式(14)估算结果基本与实际计算值相等，大于 0.42时，阵宽度越小，估算误差越大，宽度为0.2 m时式(14)估算误差达到0.75 dB，但其估算准确度依然优于式(4)。实际上，工作在非常低的频率时，如100 Hz，则平面阵宽度相对于波长基本可忽略不计，此时以直线阵的指向性进行估算准确性更高。

图5 平面阵垂直波束宽度随阵宽度变化曲线Fig.5 Variation of the vertical beamwidth of planar array with array width

图6 平面阵指向性指数随阵宽度变化曲线Fig.6 Variation of the directivity index of planar array with array width

2.4 适用性扩展分析

由于其他非规则阵、曲面阵等阵形的指向性指数无法通过解析计算方式得到估算公式，因此一般采用平面阵指向性指数估算公式对其他面阵、体积阵的指向性指数进行估算。本文通过仿真分析，验证式(14)对其他阵形指向性指数的估算准确度。

以圆柱阵为例，设圆柱阵直径为4 m，高为4 m，阵元间距为0.1 m，波束形成时采用正对主极大方向120°扇面的阵元，则不同信号频率下指向性指数计算值和估算值变化情况如图8所示，其中估算时有效面积取 1/3扇面对应的最大投影面积，即

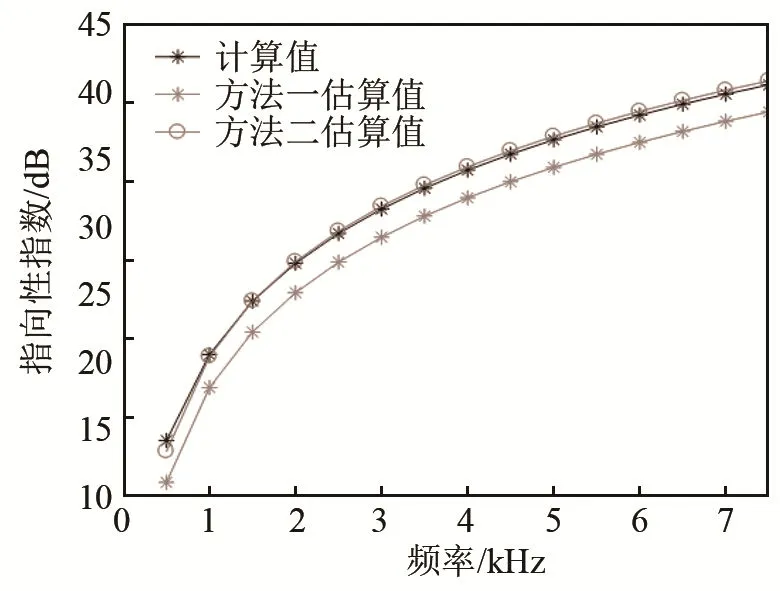
图8 圆柱阵指向性指数随阵直径变化曲线Fig.8 Variation of the directivity index of cylindrical array with array width

分析表明，采用式(14)估算公式计算圆柱阵指向性指数同样有效，其估算值在较低频率时略低于实际计算值，在中高频时略高于实际计算值，1 kHz以上时估算误差在0.25 dB以内，准确性优于采用式(4)估算结果。

同样的，式(14)指向性指数估算同样适用于梯形平面阵、球面阵等其他阵形，并具有较高的估算准确性，本文不再详细一一举例。

3 结 论

一般估算声呐作用距离时，平面阵指向性指数采用《实用声呐工程》的公式进行估算，但实际应用时发现该估算结果与实际计算值相差较大，导致估算声呐性能产生偏差。本文在离散平面阵指向性指数与连续平面阵指向性指数近似相等、阵孔径远大于波长时波束能量集中于主极大附近两个前提条件下，对平面阵的指向性指数估算公式进行推导和改进。当平面阵满足以上条件时，改进公式计算的指向性指数与理论公式计算的指向性指数真值相比，仅有很小的偏差。对偏离假设条件的情况做了分析，在阵孔径减小时指向性指数估算偏差逐渐增大。最后，本文将该公式在圆柱阵应用情况做了分析，证明该公式在圆柱阵上应用依然具有较高的准确度。后续将继续研究该估算公式对球阵、共形阵等阵形的指向性指数具体估算的适用性分析，以用于更多的声呐性能计算。