一类渐近非扩张映射不动点的粘滞逼近方法

魏　超

(南京财经大学 应用数学学院, 江苏 南京　210023)

一类渐近非扩张映射不动点的粘滞逼近方法

魏超

(南京财经大学 应用数学学院, 江苏 南京210023)

摘要:研究了一类渐近非扩张映射不动点问题的迭代算法.通过利用粘滞逼近方法及渐进非扩张映射,在具有一致凸的Banach空间中获得了新的迭代序列,并且证明了该迭代序列的强收敛性.

关键词:渐近非扩张映射; 压缩映射; 不动点; 粘滞逼近; 强收敛

0引言

近年来,非扩张及渐近非扩张映射不动点的逼近迭代技巧已被学者广泛研究[1-8].2007年,Wang[9]提出了一种Hilbert空间中非扩张映射的hybrid迭代方法,给出了不动点收敛定理.同年,Osilike等[10]在hybrid迭代方法基础上,通过不使用hybrid算子中强单调的假定,在任意Banach空间中扩展了Wang的结果.2012年,Qiu等[6]推广了Song等[4]的结果,并且给出了强收敛定理.2015年,Yolacan等[11]在Banach空间中讨论了逼近渐近非扩张映射不动点的迭代格式: 对任意给定点u∈K,由下式计算{xn}

xn+1=αnu+βnxn+γn[Tnxn-λn+1μA(Tnxn)],∀n≥0

(1)

其中{αn},{βn},{γn}为[0,1)中的实数序列,且αn+βn+γn=1,n≥1.并在适当条件下证明了式(1)序列的强收敛性.

本文在Yolacan等[12]基础上,建立了一个改进的渐近非扩张映射不动点的粘滞逼近方法:

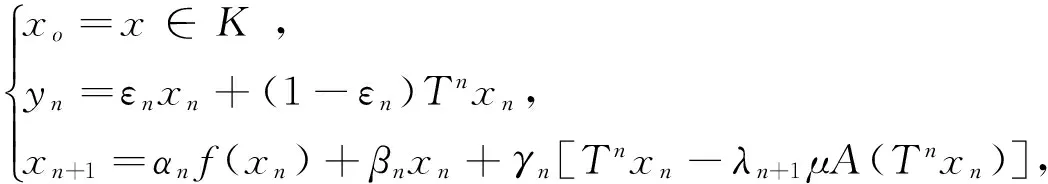
(2)

其中{αn},{βn},{γn}为[0,1]中的实数序列,{εn}为[0,1]中的实数序列,T,f,A分别为本文预备知识里所定义的渐近非扩张映射、具有ρ系数的压缩映射及L-Lipschitzian映射.在一定条件下,证明了该方法所得到的迭代序列的强收敛性.所得结果改进推广了Yolacan等[11]提出的相应结论.

1预备知识

在本文中,需要用到Banach空间一致凸及一些映射的相关概念.具体定义如下:

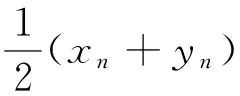
定义2设E为一实Banach空间,K为E的一个非空闭凸子集.

1) 若映射T:K→K满足:‖Tx-Ty‖≤‖x-y‖,(∀x,y∈K).则称T为非扩张映射.记F(T)为T的不动点集,即F(T)={x∈K:Tx=x};

2) 若存在一个常数L>0,使得‖Tx-Ty‖≤L‖x-y‖成立,(∀x,y∈K).则称T为L-Lipschitzian映射;

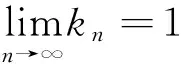
4) 若映射f:K→K,存在一个实数ρ∈(0,1)并且满足‖f(x)-f(y)‖≤ρ‖x-y‖,∀x,y∈K,则称f为具有系数ρ的压缩映射.

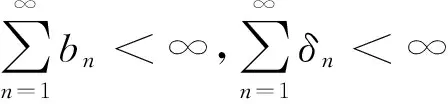
为了给出本文第三部分相关定理的证明,还需用到以下两个引理:

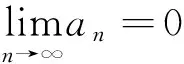
2主要结果

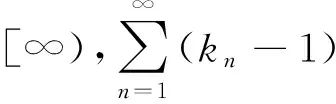
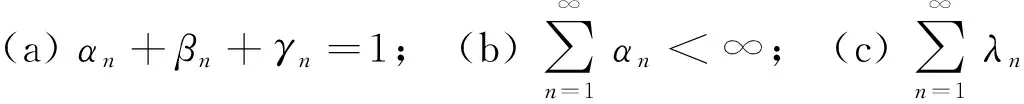
则有

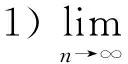
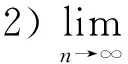
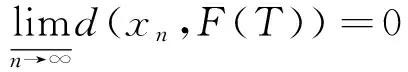
证先证 1),设p∈F(T),由T的渐近非扩张性得

‖yn-p‖≤εn‖xn-p‖+(1-εn)‖Tnxn-p‖≤

εn‖xn-p‖+(1-εn)kn‖xn-p‖≤kn‖xn-p‖.

对于∀n≥0,由T的渐近非扩张性，f的压缩性和A的L-Lipschitzian性,有

‖xn+1-p‖=‖αnf(xn)+βnxn+γn[Tnxn-λn+1μA(Tnyn)]-p‖≤

αn‖f(xn)-p‖+βn‖xn-p‖+γn‖[Tnxn-λn+1μA(Tnyn)]-p‖≤

αn‖f(xn)-f(p)‖+αn‖f(p)-p‖+βn‖xn-p‖+

γn‖Tnxn-p‖ +γnλn+1μ‖A(Tnyn)‖ ≤

ραn‖xn-p‖+αn‖f(p)-p‖+βn‖xn-p‖+γnkn‖xn-p‖ +

γnλn+1μ‖A(Tnyn)-A(p)+A(p)‖≤

αn‖xn-p‖+βn‖xn-p‖+γnkn‖xn-p‖+γnλn+1μknL‖yn-p‖ +

γnλn+1μ‖A(p)‖+αn‖f(p)-p‖≤

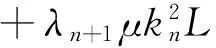
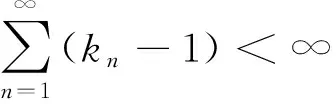
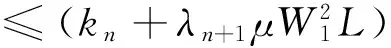
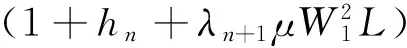
(3)

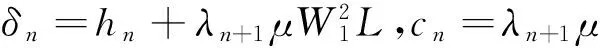
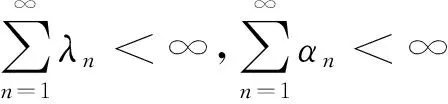
再证2),由于‖xn-p‖有界,故存在W2>0,使得

‖xn-p‖≤W2,∀n≥1

(4)

假定

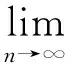
(5)

由式(5)有

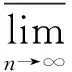
(6)

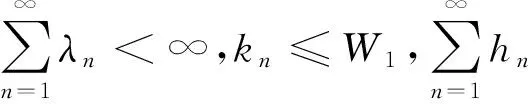
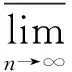
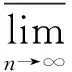
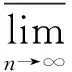
(7)

因此由式(5)～(7)及引理2,可得

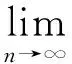
(8)

由条件(b)及式(8),可得

‖xn+1-xn‖=‖αnf(xn)+βnxn+γn[Tnxn-λn+1μA(Tnyn)]-xn‖≤

αn(‖f(xn)-f(p)‖+‖f(p)-p‖+‖p-xn‖) +

γn‖[Tnxn-λn+1μA(Tnyn)]-xn‖ ≤αn[(ρ+1)‖xn-p‖+‖f(p)-p‖]+

γn‖[Tnxn-λn+1μA(Tnyn)]-xn‖→0,(n→∞)

(9)

由条件(c)及式(8),同样可得

‖xn-Tnxn‖≤‖xn-[Tnxn-λn+1μA(Tnyn)]‖+‖[Tnxn-λn+1μA(Tnyn)]-Tnxn‖≤

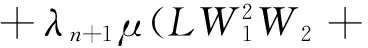
(10)

由式(9)和(10),可得

‖xn-Txn‖≤‖xn-Tnxn‖+‖Tnxn-Txn‖≤‖xn-Tnxn‖+k‖Tn-1xn-xn‖≤

‖xn-Tnxn‖+k(‖Tn-1xn-Tn-1xn-1‖+‖Tn-1xn-1-xn-1‖+‖xn-1-xn‖)≤

‖xn-Tnxn‖+k(kn-1‖xn-xn-1‖+‖Tn-1xn-1-xn-1‖+‖xn-1-xn‖)→0,(n→∞)

(11)

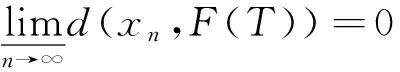
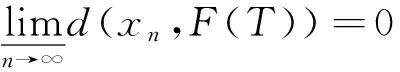
由式(3)可得

‖xn+1-p‖≤(1+δn)‖xn-p‖+cn=‖xn-p‖+ωn

(12)

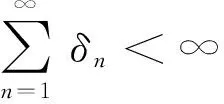
d(xn+1,F(T))≤d(xn,F(T))+ωn

(13)

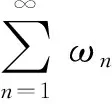
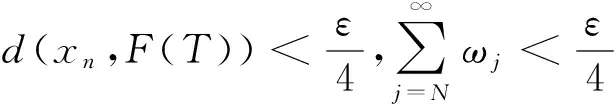
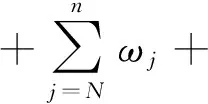
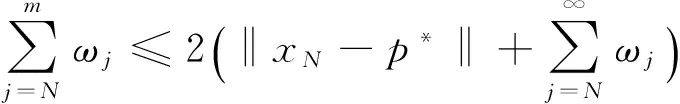
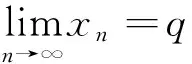
至此定理得证.

注1该定理从迭代格式角度推广了Yolacan等[12]的工作.

注2该定理不同于唐艳[14]所讨论的.我们讨论的是一致凸的实Banach空间,而后者讨论的是一致Gateaux可微范数的Banach空间.另外本定理中的迭代格式也不同于后者.

在迭代格式(2)中,若εn=0,式(2)变为如下迭代格式

xn+1=αnf(xn)+βnxn+γn[Tnxn-λn+1μA(T2nxn)]

(14)

我们可以得到如下定理.

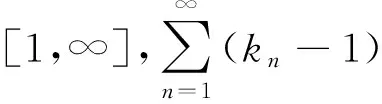
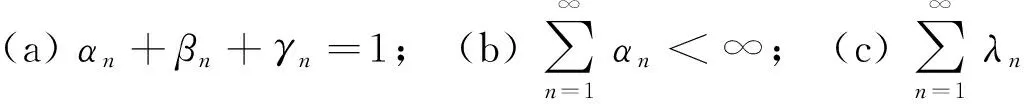
则有

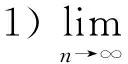
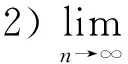
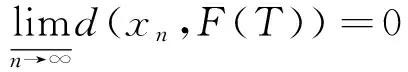
证先证 1).设p∈F(T).对于∀n≥0,由T的渐近非扩张性,f的压缩性和A的L-Lipschitzian性,有

‖xn+1-p‖=‖αnf(xn)+βnxn+γn[Tnxn-λn+1μA(T2nxn)]-p‖≤

αn‖f(xn)-p‖+βn‖xn-p‖+γn‖[Tnxn-λn+1μA(T2nxn)]-p‖≤

αn‖f(xn)-f(p)‖+αn‖f(p)-p‖+βn‖xn-p‖+γn‖Tnxn-p‖+

γnλn+1μ‖A(T2nxn)‖≤ραn‖xn-p‖+αn‖f(p)-p‖+βn‖xn-p‖+γnkn‖xn-p‖ +

γnλn+1μ‖A(T2nxn)-A(p)+A(p)‖ ≤αn‖xn-p‖+βn‖xn-p‖+γnkn‖xn-p‖+

γnλn+1μk2nL‖xn-p‖+γnλn+1μ‖A(p)‖ +αn‖f(p)-p‖≤

kn‖xn-p‖+λn+1μk2nL‖xn-p‖+λn+1μ‖A(p)‖+αn‖f(p)-p‖.

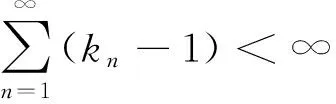
‖xn+1-p‖≤(kn+λn+1μW1L)‖xn-p‖+cn≤

(1+hn+λn+1μW1L)‖xn-p‖+cn≤(1+δn)‖xn-p‖+cn

(15)

其中δn=hn+λn+1μW1L,cn=λn+1μ‖A(p)‖+αn‖f(p)-p‖.

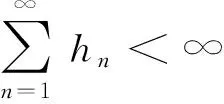
再证2), 3).由定理1类似可证.在式(2)中,若εn=1,式(2)变为迭代格式:

xn+1=αnf(xn)+βnxn+γn[Tnxn-λn+1μA(Tnxn)

(16)

则有如下定理.

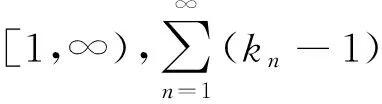
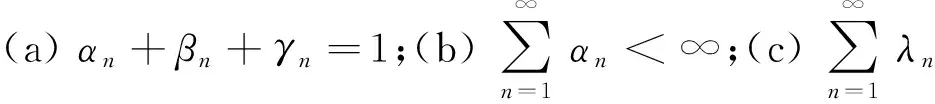
则有

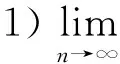
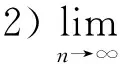
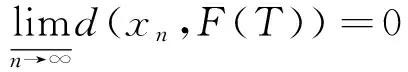
证由定理2类似可证.

参考文献：

[1]Khan S H, Fukhar-Ud-in H.Weak and strong convergence of a scheme with errors for two nonexpansive mappings[J].Nonlinear Anal,2005,61(8):1295-1301.

[2]Suzuki T.Strong convergence of Krasnoselskii and Mann's type sequences for one parameter nonexpansive semigroups without Bochner integrals[J].J Math Anal Appl,2005,305(1):227-239.

[3]Jung J S.Iterative approaches to common fixed points of nonexpansive mappings in Banach spaces[J].J Math Anal Appl,2005,302(2):509-520.

[4]Song Y, Chai X.Halpern iteration for firmly type nonexpansive mappings[J].Nonlinear Anal,2009,71(10):4500-4506.

[5]Feng G.A new hybrid iteration method for a finite family of asymptotically nonexpansive mappings in Banach spaces[J].Fixed Point Theory and Applications，2013,2013(1):1-10

[6]Qiu L H, Yao S S.Hybrid iteration method for fixed points of nonself nonexpansive mapping in real Banach spaces and its applications[J].Inter Math Forum,2012,7(6):251-258.

[7]Schu J.Weak and strong convergence to fixed points of asymptotically nonexpansive mappings[J].Bull Aust Math Soc,1991,43(4):153-159.

[8]Xu H K.Another control condition in an iterative method for nonexpansive mappings[J].Bull Aust Math Soc,2002,65(1):109-113.

[9]Wang L.An iteration method for nonexpansive mappings in Hilbert spaces[J].Fixed Point Theory Appl,2007,2007(1):151-154

[10]Osilike M, Isiogugu F, Nwokoro P.Hybrid iteration method for fixed points of nonexpansive mappings in arbitrary Banach spaces[J].Fixed Point Theory Appl,2008,2008(1):1-7.

[11]Yolacane, Kiziltunc H.Convergence theorems of a hybrid iteration method for fixed points of asymptotically nonexpansive mappings[J].Adv Fixed Point Theory,2015,5(1):110-119.

[12]ClarksonL J A.Uniformly convex spaces[J].Trans Amer Math Soc,1936,40(3):396-414.

[13]Tan K K, Xu H K.Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process[J].J Math Anal Appl,1993,178(2):301-308.

[14]唐艳.Banach空间中非扩张映射不动点的粘性逼近方法[J].数学杂志,2013(1):99-104.

[责任编辑：李春红]

A Viscous Approximation Method for Fixed Point of a Class of Asymptotically Nonexpansive Mappings

WEI Chao

(School of Applied Mathematics Nanjing University of Finance and Economics, Nanjing Jiangsu 210023, China)

Abstract:In this paper, we study the iterative method for approximating the fixed point of asymptotically nonexpansive mappings. By using the viscous approximation method, the strong convergence of the iterative sequence is obtained in a real uniformly convex Banach space.

Key words:asymptotically nonexpansive mappings; contraction mapping; fixed point; viscous approximation method; strong convergence

收稿日期:2015-11-14

通讯作者:魏超(1991-), 男, 江苏淮安人, 硕士研究生, 研究方向为非线性分析及其经济应用. E-mail: 582836071@qq.com

中图分类号:O177.91

文献标识码:A

文章编号:1671-6876(2016)02-0099-05