余弦函数的Perron定理

卢丑丽

(山西农业大学 信息学院, 山西 晋中　030800)

余弦函数的Perron定理

卢丑丽

(山西农业大学 信息学院, 山西 晋中030800)

摘要:研究了二阶微分方程的柯西问题,利用余弦函数的指数有界性和泛函分析方法,得到关于该问题的Perron定理,推广了相关文献的主要结论.

关键词:柯西问题; 余弦函数; 二阶微分方程; 指数性

0引言

1921年,J.Hadamard在《偏微分方程中的柯西问题》中首次介绍了柯西问题, 紧接着, 经典的柯西问题(ACP;A,X)

被广泛研究[1-3].当算子A生成一个强连续C0半群或者C半群时,其指数有界的解的问题及应用被进一步的研究.O.perron[4]给出了指数有界的特征,并且指出,当X是有限维空间,A是一个矩阵时,对任意R+到X的连续有界函数,满足柯西问题(A,x)

的解是指数稳定的之后,结合C0半群或者C半群的相关结论被推广到无穷维空间,非自治系统等情形.2004年,P.Preda[5]研究了C半群的perron问题,但二阶柯西问题的perron问题是否存在并未提及.本文借助余弦函数及其性质,并应用相关知识,得到二阶柯西问题的指数稳定解的perron定理,其中二阶Cauchy问题微分方程为

(1)

1预备知识

本文中假设(X,‖·‖)为Banach空间,其中‖·‖是最大范数,记B(X)为X上全体有界线性算子构成的Banach代数,Cb(R,X)为f:R→X上全体有界且一致连续函数.C0(R,X)是满足limt→∞f(t)=0的所有连续函数,AP(R,X)为Cb(R,X)中满足{t→eiλtx:R→X,λ∈R,x∈X}的线性闭包.

定义1设(X,‖·‖)为Banach空间,X中的强连续算子族{C(t):R→B(X)}称为余弦算子函数(简称余弦函数),如果满足

1) C(t+s)+C(t-s)=2C(t)C(s),∀t,s∈R;

2) C(0)=I,I为单位算子;

3) 对R中任意固定的x∈X,算子t→C(t)x是强连续的.

性质1[4]1) C(t)=C(-t),∀t∈R,S(t)=-S(-t),∀t∈R;

2) C(t)C(τ)=C(τ)C(t),S(t)S(τ)=S(τ)S(t),∀t,τ∈R;

3) C(0)=I,S(0)=0;

4)∃M≥1,ω>0,s.t.‖C(t)‖≤Meω|t|,∀t∈R.

5) 如果A是余弦函数C(t)的无穷算子,则A是闭稠定的,且满足∀t∈R,C(t)D(A)⊂D(A), 及 ∀g∈D(A),C(t)Ag=AC(t)g.

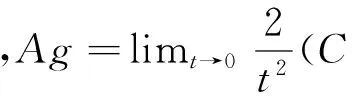
8) 如果A是余弦函数C(t)的无穷算子,则

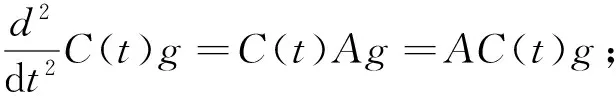
本文考虑空间X中如下的二阶微分方程

其中A是余弦函数{C(t),t∈R}的算子,f为从R到X的连续函数,显然柯西问题(1)的古典解u(t)二阶可微,u(t)∈D(A),并满足方程(1).

证假设u:R→D(A)⊂X是(1)的解,则从文[3]可知

-S(t-s)Au(s)+C(t-s)u′(s),

对上式从0到t积分,同时由于C(0)=I,S(0)=0,有

定义4Cb(R,X)的一个子集E称为连续可分的,如果对于任意的a>0,以及任意的从[-a,a]到X的映射f,存在g∈E满足‖g‖=supt∈[-a,a]|f(t)|及g|[-a,a]=f.

例1对于一个给定a>0及从[0,a]到X的连续函数,我们定义g:R→X,g(-t)=g(t),

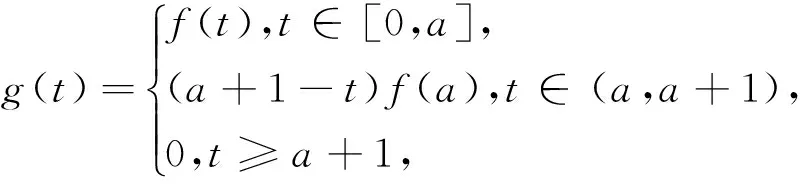
则g∈C0(R+,X)⊂B∪C(R+,X),g|[0.a]=f,且‖g‖=supt∈[0,a]‖f(t)‖.故C0(R,X),

Cb(R,X),AP(R,X)是连续可分的.

性质3假设{C(t),t∈R}是算子A生成的余弦函数,如果E是可容许{C(t)}闭集的一个子空间,则存在K>0满足‖uf′‖≤K‖f‖,∀f∈E.

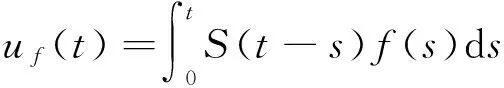
故VEf=g.结论得证.

2主要结论

定理1如果E是Cb(R,X)中连续可分的闭子空间,且E上对余弦函数{C(t),t∈R}指数有界是可容许的,则{C(t),t∈R}是指数稳定的.

证首先我们证明{C(t),t∈R}是有界的.

因为余弦函数为偶函数,对任意t≥0,x∈X,及函数f:[0,t]→X定义f(s)=e-ωsC(s)x,则存在函数g∈E使得g|[0,t]=f,及‖g‖=sups∈[0,t]‖f(s)‖≤M‖x‖.

故有

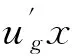
即对任意t≥0,当L=M(2ωK+1),‖C(t)‖≤L.

其中t≥0和x∈X均为任意,则存在gn∈E使得

gn|[0,t]=fn,‖gn‖=sups∈[0,t]‖fn(s)‖≤LKn‖x‖.

从而

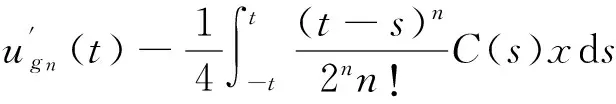
因此

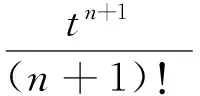
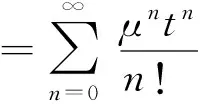
证完.

定理2假设{C(t)}t≥0是指数有界余弦函数,若满足以下条件之一,则其是指数稳定的.

1) C0(R,X)对{C(t)}t≥0可容许的;

2) B∪C(R,X)对{C(t)}t≥0可容许的;

3) AP(R,X) 对{C(t)}t≥0可容许的.

证因f∈C0(R,X),易知函数有界.再由定理1及例1易证结论.

注我们考虑C余弦函数,可得类似的结论.

参考文献：

[1]Pazy A. Semigroups of linear operators and applications to partial differential equations[M].New York: Springer-Verlag, 1983.

[2]李延保,秦国强,王在华. 有界线性算子半群应用基础[M].沈阳:辽宁科学技术出版社, 1992.

[3]陆凤玲,宋晓秋,王甫红.C半群及柯西问题的温和解[J].徐州师范大学学报, 2008, 26(4):35-37.

[4]王如海,雷呈凤, Banach空间中算子余弦函数的一个特征[J].南昌航空工业学院学报, 1999, 13(2):49-53.

[5]Petre Preda,Alin Pogan, Ciprian Preda. The Perron problem for C-semigroups[J]. Math J Okayama Univ, 2004(46):141-151.

[6]郑权,雷岩松.指数有界的C余弦函数[J].系统科学与数学, 1996, 16(3):242-252.

[责任编辑：李春红]

The Perron Problem of Cosine Functions

LU Chou-li

(School of Information, Shanxi Agricultural University, Jinzhong Shanxi 030008, China)

Abstract:This paper deals with the problem on the second-order differential equation, using the theory of the cosine function with the exponentially bounded and the method of functional analysis, the perron problem of the second order differential equation is given. And extend the main results of corresponding papers.

Key words:abstract cauchy problem; cosine functions; second-order diferential equation; exponentially

收稿日期:2015-11-09

通讯作者:卢丑丽(1985-), 女, 山西忻州人, 肋教, 硕士, 研究方向为应用泛函分析. E-mail: 290136842@qq.com

中图分类号:O175.3

文献标识码:A

文章编号:1671-6876(2016)02-0110-04