丁坝群附近流场的三维数值模拟研究

□郭晓峰　□杨　兰（蚌埠学院）



丁坝群附近流场的三维数值模拟研究

□郭晓峰□杨兰（蚌埠学院）

摘要：丁坝具有导流、护岸、调整水深和营造局部冲淤等众多功能，在实际工程中应用广泛。文章采用有限体积法对正挑丁坝群的周围流场分布进行了三维数值模拟，以期深化对丁坝群附近的水流流场及局部冲刷机理的认识。研究发现，流场中有三个大的逆时针旋涡产生，第一座丁坝坝头处有下潜水流，且切应力达到最大值，是该位置发生严重冲刷的主要原因，且流量越大，冲刷越严重。

关键词：丁坝群；数值模拟；流场分布；局部冲刷

0　前言

丁坝是一种兼有导流、护岸、调整水深和营造局部冲淤等众多功能的水工建筑物，实际工程中除了个别情况采用单丁坝外，大多情况下都采用丁坝群来达到河道整治效果［1］。丁坝群修建后，改变了其周围的水流形态，产生旋涡、回流等一系列现象，流动结构非常复杂。因此，研究丁坝附近的流场具有重要的工程意义。

到目前为止，关于丁坝的研究，已经取得了一些成果。例如曹艳敏等通过超声多普勒测速仪，对已形成冲刷坑情况下的丁坝流场和紊动动能进行了三维测量；魏文礼等采用RNG湍流模型对梯型断面明渠非淹没式丁坝的水力特性进行了三维数值模拟，模拟结果与实验结果吻合良好，反映出了非淹没式梯形断面丁坝流动特性的变化规律；高先刚等采用试验的方法对双丁坝的最佳间距进行了研究，给出了丁坝群间距的遵循规律；许慧等对长江下游的淹没丁坝群进行了二维水流数值模拟，模拟结果与实际工程实测资料吻合良好；Jennifer Duan通过实验和数值模拟的方法对与水流方向夹角为150°的丁坝群进行了研究，发现第一座丁坝坝头处的冲刷最严重。以往的研究大部分都是采用实验的方法，且对单丁坝的研究较多，关于丁坝群三维数值模拟研究还相对较少，对于丁坝附近局部冲刷坑形成的机理有待深入研究。基于此，文章采用RNG湍流模型对非淹没丁坝群周围的流场进行三维数值模拟，通过分析丁坝群周围的流场，假设对其局部冲刷机理的认识。

1　计算模型

1.1数学模型

1.1.1控制方程

丁坝群流场三维流动的控制方程为连续性方程和动量方程：

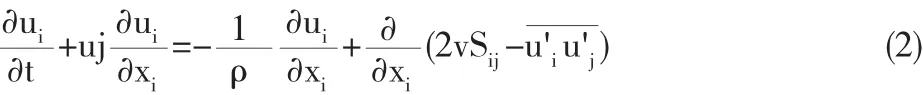
其中，

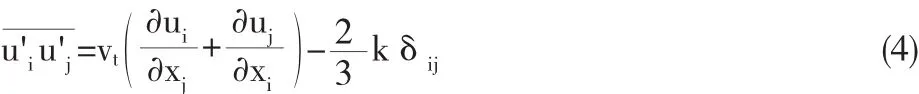
式中，ui为i方向的分速度，u'i为i方向的脉动速度，P为压力，Sij为应变率张量，u'iu'j为雷诺应力张量，ρ是流体密度，v为动力粘度，vt为湍流粘度，k是湍动能，δij是克罗内克符号（δij=1，i-j；δij=0，i≠j）。

1.1.2湍流模型

文章的模拟计算采用RNG湍流模型，该模型是由Yakhot，Orszag于1986年提出的一种改进的湍流模型，模型中的系数是由理论分析得到的，模型考虑到了湍流旋涡，精度较高。其控制方程为：

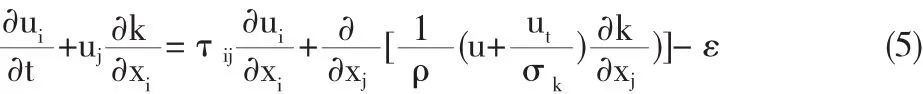
1.2网格系统及数值方法

计算区域长3 m，宽0.60 m，高0.30 m，糙率为0.01。丁坝群位于左岸，垂直于水流方向，丁坝间距为0.30 m，丁坝长0.15 m，宽0.01 m，为非淹没丁坝。文章对流量分别为0.01 m3/s、0.04 m3/s 和0.06 m3/s三种工况下的丁坝群进行了计算。

计算时采用结构化非均匀矩形网格进行划分，对丁坝群附近的网格进行了加密，总网格数约为130万。采用有限体积法离散控制方程，湍流模型为RNG模型。上游设为速度进口，三种流量给定对应的平均速度，分别为0.14 m/s、0.29 m/s、0.41 m/s；出口设为自由出流；上表面采用VOF法来捕捉自由面；固体边壁为无滑移壁面，近壁面采用标准壁面函数进行处理。

2　数学模型及数值方法

经计算发现，0.01 m3/s、0.04 m3/s和0.06 m3/s三种流量时对应的流线、流速（包括总速度和三个方向的分速度）的分布规律基本相似，只是对应的数值有所不同，现以流量为0.04 m3/s时的流场为例进行详细的分析。

2.1流线分布

图1所示为丁坝群周围的流线分布，由图可以看出，第一座丁坝的挑流效果非常明显，第二座丁坝处于第一座丁坝的尾流中，没有起到明显的挑流作用，随着距离的增加，水流逐渐恢复，第三座丁坝又起到了挑流的效果。整个流场中有三个大的逆时针旋涡产生，前两座丁坝之间的旋涡中心都处于两坝的正中间，形状接近方形，而下游尾流区的旋涡为不规则的椭圆形。尾流旋涡中心与第三座丁坝的距离约为0.30 m。

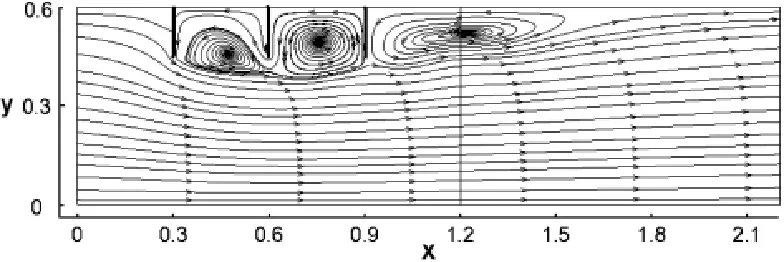
图1　流线分布图

2.2流速分布

经计算，分析丁坝群附近的总速度及三个方向（横向、纵向和流向）分速度的分布可以得出，由于丁坝群的存在，束窄了河道过水断面面积，使得单宽流量增加，主流区速度增大，最大流速达到0.54 m/s。随着距离的增加，水流逐渐恢复。丁坝群间x向（即横向）分速度出现负值，说明此处有旋涡存在，水流与主流方向相反。y向（即纵向）速度在整个流场内都很小，在第一座丁坝坝头处出现负的最大值，表明第一座丁坝将水流挑向右岸。z向（即垂向）速度同样在第一座丁坝坝头处出现负的最大值，表明此处水流方向向下，即存在较明显的下潜水流。

2.3湍动能及湍动能耗散率

湍动能是表征流体湍动的程度，湍动能越大，说明流体湍动越剧烈，湍动强度越大。计算得到流场中大部分区域的湍动能都很小，相应的这些区域各个方向的脉动速度也都很小，故而湍动能的值较小。在湍流流动中，湍动能耗散率越大，相应的能量损失也就越大。湍动能耗散率和湍动能的分布相似，最大值均出现在第一座丁坝的坝头处，这是因为第一座丁坝坝头处水流复杂，水流之间的粘滞力大，故湍动能和湍动能耗散率也大。

2.4河床切应力

河床切应力直接作用在床沙质的表面，推移质输沙率与河床切应力成正比。图2所示为计算得到的三座丁坝坝头所在断面的河床切应力分布，由图可以看出，第一座丁坝坝头处切应力达到最大值，而在后面两个丁坝坝头处切应力相对较小。因此，第一座丁坝坝头处形成冲刷坑的可能大于其他两个丁坝。图3为不同流量下第一座丁坝所在断面切应力分布，可以看出随着流量的增加，切应力的数值也随之增加，故流量越大，冲刷可能会更严重。

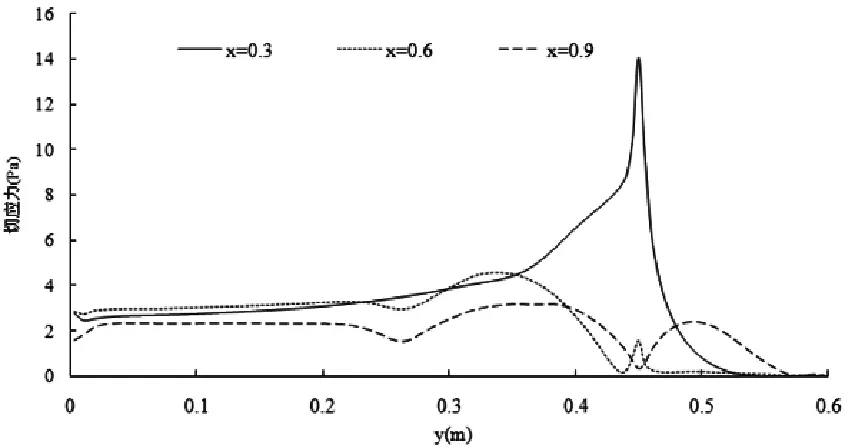
图2　丁坝所在横断面河床切应力分布图

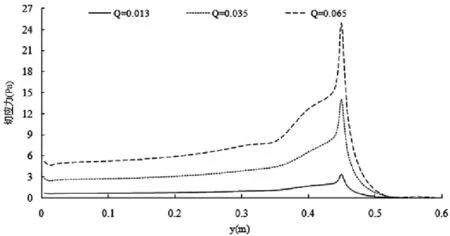
图3　不同流量下第一座丁坝所在断面切应力分布图

3　结论

文章通过有限体积法对丁坝群周围的流场进行三维数值模拟，分析了流线、流速和河床切应力的分布情况。研究发现第一座丁坝的挑流效果非常明显，丁坝群间存在三个大的逆时针旋涡，旋涡处的流速较小。第一座丁坝坝头处切应力达到最大值，垂向速度为负值，说明有下潜水流的存在，这两个因素是造成此处冲刷的主要因素，且流量越大，冲刷越严重。

参考文献

［1］李冰冻，李嘉，李克锋.丁坝水流的水槽试验及数值模拟研究［J］.水动力学研究与进展，A辑，2013，28（2）：176-183.

［2］陈稚聪，黑鹏飞，丁翔.丁坝回流分区机理及回流尺度流量试验研究［J］.水科学进展，2008，19（5）：613-617.

（责任编辑：左英勇）

中图分类号：TV135

文献标识码：A

文章编号：1673-8853（2016）04-0106-02

基金项目：国家级大学生创新创业训练计划项目（201411305032），蚌埠学院院级自然科学研究项目（2015ZR04，2014ZR10）

作者简介：郭晓峰（1992-），男，主要从事水利水电、水力学及河流动力学方面研究工作。

收稿日期：2016-01-21