二分类集群数据下灵敏度和特异度的置信区间构建
霍 剑
(中国人民大学 统计学院,北京 100872)
二分类集群数据下灵敏度和特异度的置信区间构建
霍剑
(中国人民大学 统计学院,北京 100872)
摘要:在医学诊断等应用领域中广泛存在二分类集群数据,其特征是来自同一个群的反应结果存在相关。对于该数据下灵敏度和特异度的置信区间构造,目前已有方法在小样本及灵敏度或特异度偏大时区间覆盖率较差,通过利用二项分布得分区间的构造思想,基于灵敏度和特异度的最优加权估计量构造一种新的置信区间;通过蒙特卡洛模拟表明,与已有方法相比新区间的覆盖率明显最优、且区间长度较小;新区间在二分类集群数据的应用中值得推广。
关键词:集群数据;灵敏度;特异度;置信区间
一、引 言
集群数据(clustered data)普遍存在于医学诊断、放射研究等应用领域,其关键特征是来自同一个群的反应结果存在相关。比如在医学诊断中评估某一诊断方法检测结肠息肉的灵敏度,而研究发现每个病人有多处息肉,此时统计分析的基本单位不是病人而是息肉,这样在所有病人的息肉检测结果中,每个病人是一个群,不同病人的检测结果独立,而同一病人的多个息肉检测结果存在相关;这种例子还有很多,比如评价某一牙周炎诊断方法,研究的基本单位为病人牙齿表面的某个位置,此时同一病人的多个齿面位置的诊断结果存在相关。
灵敏度和特异度是评价医学诊断精确性的重要指标。灵敏度(sensitivity,Se)是真实情况为有病时诊断发现疾病的能力,即在实际有病的条件下诊断结果为阳性的概率。特异度(specificity,Sp)是真实情况为无病时试验排除疾病的能力,即在实际无病条件下试验结果为阴性的概率,在实际应用中给出其置信区间是很有意义的。
传统的灵敏度或特异度置信区间采用的是二项分布比例置信区间,但对于二分类集群数据,由于二项分布比例置信区间没有考虑数据间的相关,而忽略相关性的推断会有偏差,导致估计的区间长度过小,因此二项分布比例置信区间无法正确应用到集群数据。目前,集群数据下灵敏度和特异度置信区间的研究较少,主要有四种构造方法注意到了灵敏度和特异度的构造方法相同[1-2],下面以灵敏度为例进行说明:Rao等人和Cochran提出了一种二分类集群数据下灵敏度方差的估计量,以此来调大置信区间长度[3][4]140-156;Donner和Klar[5]168-175[6]通过方差膨胀因子给出了另一种集群数据下的灵敏度的方差估计量;Lee和Dubin通过等加权于个体构造了灵敏度估计量,并以此构造置信区间[7-8];Jun和Ahn则通过最小化灵敏度估计量的方差,给出了一种最优加权形式的灵敏度估计量,并以此构造置信区间[2]。这里将四种方法构造的置信区间依次记为Rao-Scott区间、Donner-Klar区间、Lee-Dubin区间和Jun-Ahn区间,这四种区间都是以Wald方法思想而构造的置信区间,而这些区间在样本量较小及当真实灵敏度或特异度偏大时覆盖率较差。针对目前方法的不足,本文从新的角度,通过利用二项分布得分区间的构造思想,基于灵敏度(特异度)的最优加权估计量提出一种新的二分类集群数据灵敏度(特异度)置信区间,并通过数值模拟及实际应用,结果表明新构造的区间比其他四种区间有明显的优势,不仅达到了更好的区间覆盖率,同时区间长度整体较小。
二、置信区间的提出
(一)已有方法的介绍

(1)
其中z1-α/2是标准正态分布的上α/2分位数,上式为Se的100(1-α)%置信区间。
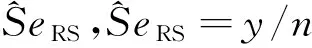
(2)

(3)
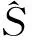
(4)
注意到如果每个个体的ni都相同时,则与Rao-Scott区间等同。
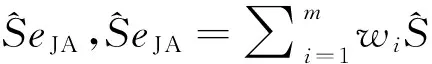
(5)
(二)新方法的提出

Var(yi)=Se(1-Se)ni(1+(ni-1)ρ)
从而有:

(6)
(7)
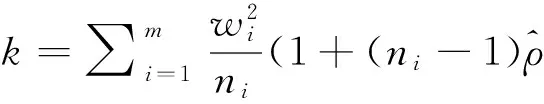
(8)
其中z=z1-α/2,新区间形式类似二项分布得分区间。
三、蒙特卡洛数值模拟
为了研究新构造的置信区间表现,考虑用蒙特卡洛数值模拟比较已有四种区间和新区间,通过区间覆盖率(CP)和区间期望长度(EL)两个指标评价五个区间的表现。区间覆盖率越接近预先设定的置信水平,区间的表现越好,同时在区间覆盖率较好控制下,区间期望长度越小越好[13]。
这里考虑不同的情形:不同的个体数m=10、20、50;不同的真实灵敏度或者特异度,这里以灵敏度为例,Se=0.5、0.6、0.7、0.8、0.9;不同的个体内相关系数ρ= 0.1、0.2、0.5,即分别考虑不同的样本量、灵敏度和个体内相关性。具体模拟过程为,假定第i个个体有ni个病变位置,即有ni个试验结果,ni从均匀分布U[1,8]中随机取整得到,第i个个体阳性的试验结果总数yi从beta-binomial分布中生成[2,14],即yi~binomial(ni,Sei),Sei~beta(αi,βi),其中αi=Se(1-ρ)/ρ,βi=(1-Se)(1-ρ)/ρ。重复模拟5 000次,计算区间覆盖率和区间期望长度,模拟结果见表1。表1中将Rao-Scott区间、Donner-Klar区间、Lee-Dubin区间、Jun-Ahn区间和新区间分别简称为RS、DK、LD、JA和NEW。
对于区间覆盖率(CP),从表1中看到新区间在不同情形下都比其他四种区间表现得好,特别是在样本量较少及当真实灵敏度偏大时,新区间比其他区间表现得明显要好。对于其他四种区间,Rao-Scott区间覆盖率较差;Donner-Klar区间、Lee-Dubin区间和Jun-Ahn区间整体上大致相当,这四种区间都在样本量较少及当真实灵敏度偏大时覆盖率较差;对于区间期望长度(EL),Lee-Dubin区间在ρ= 0.1、0.2时比其他区间长度上更大些, Rao-Scott区间与Donner-Klar区间除m=10情况外表现非常接近,新区间除Se=0.9外比其他区间长度明显要小,在Se=0.9时与其他区间相当,整体上看新区间长度较小。综上,通过数值模拟表明,新区间覆盖率明显优于其他区间,且区间长度整体较小。同时,类似于灵敏度,易知在不同特异度情况下也有一致的结论。考虑文章篇幅,这里只列了95%置信区间的模拟结果,90%置信区间也有一致的结论。
四、实际数据应用
本文实际数据来自Hujoel等人[15],该数据是用来分析某种酶诊断测试的灵敏度和特异度,这种酶测试可以检测个体牙齿的各个位置是否感染,同时用金标准对每个个体的各个位置进行了确诊。该数据具体为:在29个个体样本中,对于每个个体,在确诊为感染的位置上用酶测试检验的真阳性结果个数比该个体感染位置总数,分别为:3/6、2/6、2/4、5/6、4/5、5/5、4/6、3/4、2/4、3/4、5/5、4/4、6/6、3/3、5/6、1/2、4/6、0/4、5/6、4/5、4/6、0/6、4/5、3/5、0/2、2/6、2/4、5/5、4/6。在21个个体样本中,对于每个个体,在确诊为未感染的位置上用酶测试检验的真阴性结果个数比该个体未感染位置总数,分别为:0/1、3/3、1/2、3/3、1/1、 2/3、3/3、1/1、0/1、2/3、2/3、1/1、0/1、1/3、1/1、2/2、4/4、3/3、5/5、1/1、3/3。
表2给出了五种区间计算的酶测试灵敏度和特异度的95%置信区间,可以看出在相同的置信水平下, Lee-Dubin区间的长度最长;Rao-Scott区间与Jun-Ahn区间长度偏小些;新区间长度与其他区间相比,在灵敏度区间上最短、在特异度区间上居中。

表2 五种区间计算的酶测试灵敏度和特异度置信区间表
五、结论
对于医学诊断、放射研究等领域中常见的二分类集群数据,本文介绍了目前主要的四种灵敏度和特异度置信区间,针对目前区间在样本量较小及当真实灵敏度或特异度偏大时表现的不足,通过利用二项分布得分区间的构造思想,提出了一种新的置信区间;蒙特卡洛数值模拟研究表明,与已有区间相比新区间表现最优,不仅覆盖率明显改善,特别是在样本量较小及当真实灵敏度或特异度偏大的情况,且新区间长度整体较小,这一新区间在二分类集群数据的应用中值得考虑推广。
参考文献:
[1]Genders T T S, Spronk S, Stijnen T, et al. Methods for Calculating Sensitivity and Specificity of Clustered Data: A Tutorial[J].Radiology, 2012, 265(3).
[2]Jung S H, Ahn C. Estimation of Response Probability in Correlated Binary Data: A New Approach[J]. Drug Information Journal, 2000, 34(2).
[3]Rao J N K, Scott A J. A Simple Method for the Analysis of Clustered Binary Data[J]. Biometrics, 1992,48(2).
[4]Cochran W G. Sampling Techniques[M]. New York: Wiley, 1977.
[5]Fleiss J L, Levin B, Paik M C. Statistical Methods for Rates and Proportions[M]. Hoboken,NJ: Wiley, 2003.
[6]Donner A, Klar N. Confidence Interval Construction for Effect Measures Arising from Cluster Randomization Rrials[J]. J Clin Epidemiol, 1993,46(2).
[7]Lee E, Dubin N.Estimation and Sample Size Considerations for Clustered Binary Responses[J]. Stat Med, 1994,13(12).
[8]Lee E. Two Sample Comparison for Large Groups of Correlated Binary Responses[J]. Stat Med, 1996, 15(11).
[9]Zhou X H, Obuchowski N A, McClish D K. Statistical Methods in Diagnostic Medicine[M]. New York: Wiley, 2011.
[10]Wilson E B. Probable Inference, the Law of Succession, and Statistical Inference[J]. J Am Stat Assoc, 1927, 22(158).
[11]Casella G, Berger R L. Statistical Inference[M]. Boston:Cengage Learning, 2001.
[12]Ahn C, Hu F, Schucany W R. Sample Size Calculation for Clustered Binary Data with Sign Tests Using Different Weighting Schemes[J]. Stat Biopharm Res, 2011, 3(1).
[13]牛翠珍,范国良.基于梯度统计量的逆抽样下风险差的置信区间构建[J].统计与信息论坛,2014(8).
[14]Ahn H, Chen J J. Generation of Over-Dispersed and Under-Dispersed Binomial Variates[J]. J Comput Graph Stat, 1995, 4(1).
[15]Hujoel P, Moulton L, Loesche W. Estimation of Sensitivity and Specificity of Site-specific Diagnostic Tests[J]. J Periodontal Res, 1990, 25(4).
(责任编辑:郭诗梦)
Confidence Interval Construction for Sensitivity and Specificity in Binary Correlated Data
HUO Jian
(School of Statistics, Renmin University of China, Beijing 100872, China)
Abstract:Binary correlated data is common in many areas, such as medical diagnosis. In this paper we construct a new confidence interval for sensitivity (specificity) in binary correlated data. The idea of our construction came from score interval for a binomial proportion. The coverage probability of the existing methods is poor when the sample size is small and/or the true sensitivity (specificity) is large. Our proposed confidence interval greatly improves the performance in that case. With regard to the criterions of coverage probability and expected length, the new CI is better than the other four intervals in simulation studies. A real data example is also presented to show the application of our method.
Key words:binary correlated data; sensitivity; specificity; confidence interval
收稿日期:2016-01-08;修复日期:2016-04-13
基金项目:中国人民大学科学研究基金项目《生物医学大数据的统计方法基础研究》(15XNI011)
作者简介:霍剑,男,山西石楼人,博士生,研究方向:数理统计与生物统计。
中图分类号:O212.1∶O211.3
文献标志码:A
文章编号:1007-3116(2016)06-0028-05
【统计理论与方法】

