基于模糊理论的沥青路面预防性养护对策研究

张 家 宇

(辽宁省交通高等专科学校，辽宁 沈阳 110122)

基于模糊理论的沥青路面预防性养护对策研究

张 家 宇

(辽宁省交通高等专科学校，辽宁 沈阳 110122)

探讨了高速公路沥青路面预防性养护的主要对策，提出了基于模糊数学理论的沥青路面技术状况模糊评价方法，并分析了路面技术状况评价指标的隶属度函数，解决了预防性养护对策的模糊分析问题，对确定最优预防性养护对策具有一定借鉴意义。

模糊数学，高速公路，预防性养护

0 引言

近十年来，我国的高速公路建设事业迅猛发展，截至2015年年底，我国高速公路里程已经突破12万km，居世界第一。高速公路沥青路面的设计寿命一般为15年，但从我国实际情况看，一般的高速公路沥青路面在7年～8年左右就进入大面积维修和改造期，采用预防性养护措施以推迟路面大修时间并提高路网服务水平成为必然选择。沥青路面预防性养护对策的选择是一个复杂的过程，需要考虑现有路况、养护技术、施工组织、养护时机、寿命周期等多种因素，传统方法一般是专家调研、典型对策、经验确定等，这些方法过于主观，科学性不强，也容易造成有限养护资金的浪费。

在公路养护工作中，大量存在着事物之间的中间状态或过渡状态，比如某一项技术状况评价指标介于优秀和良好之间，或者某一个路段的养护对策既可以采用雾封层也可以采用碎石封层，在我们的传统数学认知中，我们只能人为划定标准或者确定对策来解决上述问题，但事实上，它们之间的界限并非如此简单或者明显。模糊数学理论把特征函数的值域由{0,1}扩张到[0，1]，引入隶属度函数使模糊概念能够用数学形式进行表达。本文将引入隶属度函数的模糊数学理论应用于高速公路沥青路面预防性养护对策确定过程中，建立养护对策模型，以期弥补现有预防性养护对策确定的不足。

1 预防性养护主要对策分析

沥青路面养护可以分为应急性养护、预防性养护和纠正性养护三种，按照美国各州公路和运输官员协会(American Association of State Highway and Transportation Officials，简称AASHTO)公路标准委员会的定义，路面预防性养护是指在不增加路面结构承载力的前提下，对结构完好的路面或附属设施有计划地采取某种具有费用效益的措施，以达到保养路面系统、延缓损坏、保持或改进路面功能状况的目的[1]。

按照现行规范JTG H20—2007公路技术状况评定标准的分类依据，沥青路面损坏主要包括龟裂、块状、纵裂、横裂、坑槽、松散、沉陷、车辙、波浪壅包、泛油、修补等11类21项，同时还包括路面平整度、抗滑性能、路面车辙和结构强度等其他评价指标，构成完整的沥青路面技术状况评价指标体系，如表1所示。

表1 沥青路面技术状况评价指标体系

国内外经常使用的高速公路沥青路面预防性养护措施包括灌缝、雾封层、碎石封层、超薄冷拌封层(稀浆封层、微表处等)、超薄热沥青罩面(OGFC,SMA等)和沥青再生技术等，这些不同的措施有不同的使用范围、使用时机和寿命周期，也会产生不同的使用效果和服务水平。在决策过程中，我们既要考虑当前的现有路况、技术水平、施工组织、养护时机等因素，也要预期这个决策对未来路面全寿命周期和费用的影响。这种对策确定过程基本取决于我们的主观经验判断，也会受到我们的知识结构、认知程度、实践经验和历史做法的影响，最终形成的对策可能是合理的，也有可能是不合理的或者有优化空间的。

2 沥青路面技术状况模糊评价

模糊数学理论起源于1965年美国自动控制专家扎德教授发表的《模糊集合(Fuzzy Sets)》的论文。康托尔集合论中论域里面的任一元素要么属于集合A，要么不属于集合A，非此即彼。但在公路养护实践中，并不是所有的评判指标体系和对策选择原则都严格遵循这种“非此即彼”的关系。扎德教授提出的模糊集合理论把特征函数的值域由{0,1}扩张到[0，1]，引入隶属函数使模糊概念的数学表达成为可能，也为我们对沥青路面技术状况进行模糊评价提供了理论依据。

我们以沥青路面技术状况指标中的路面车辙评价为案例进行分析，我们对车辙进行现场调查的调查指标是车辙深度RD，评价指标是车辙深度指数RDI，两者之间的函数关系是：

(1)

其中,RD为车辙深度，mm；RDa为车辙深度参数，采用20 mm；RDb为车辙深度限值，采用35 mm；a0为模型参数，采用2.0；a1为模型参数，采用4.0。

依据车辙深度指数RDI的得分值(0～100之间)，我们就可以得到路面车辙损坏属于优、良、中、次、差的等级，在JTG H20—2007公路技术状况评定标准中规定了RDI分值与技术状况评价等级的关系，如表2所示。

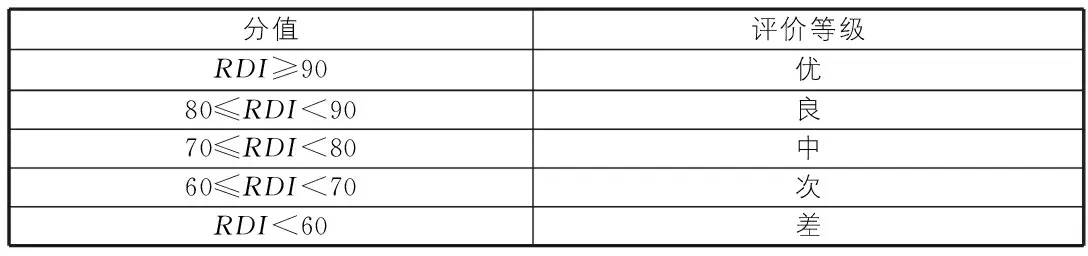
表2 公路技术状况评定标准

表2中RDI分值与评价等级之间的关系是以康托尔集合论为基础的严格意义上的分段函数，依据此函数关系，如果两条调查路段的评价指标RDI分别为80.01和79.99，尽管它们的技术状况基本相同并且完全可以采用相同对策，但由于80.01和79.99属于“良”和“中”两个不同等级，会对应完全不同的两类预防性养护手段。造成上述情况的原因是传统康托尔集合论的“非此即彼”，我们引入模糊数学中的隶属度来表达这种“亦此亦彼”的关系，并建立车辙深度指数RDI的隶属度函数。

设论域U为0～100间全体实数，A：“评价等级优秀”，A∈F(U)，则隶属度函数A(x)如下：

(2)

当x>90时,A(x)=1,即完全隶属于“优秀”等级，当x<80时,A(x)=0,即完全不隶属于“优秀”等级，而x位于80和90之间时，隶属度关系随着分值变化而变化，在本案例中隶属度关系为简单的线性关系，我们也可以根据需要设定其他的非线性函数关系。依据上述案例，我们可以分别建立“良好”“中等”“较次”“较差”其余四个等级的隶属函数，并且采用模糊集合运算获得各种的隶属关系，也可以采用适当的λ截集水平将这种模糊集合转化为康托尔集合论中的普通集合。依据上述案例，我们也可以分别对路面损坏、平整度、抗滑性能、强度等其他四项评价指标进行模糊数学分析，获得沥青路面技术状况的模糊评价体系。

3 沥青路面预防性养护对策模糊分析

如前所述，高速公路沥青路面预防性养护措施包括灌缝、雾封层、碎石封层等多种，根据工作经验，在只考虑路面损坏类型和损坏程度的简化条件下，我们建立高速公路沥青路面预防性养护技术措施决策矩阵[2]，如表3所示。

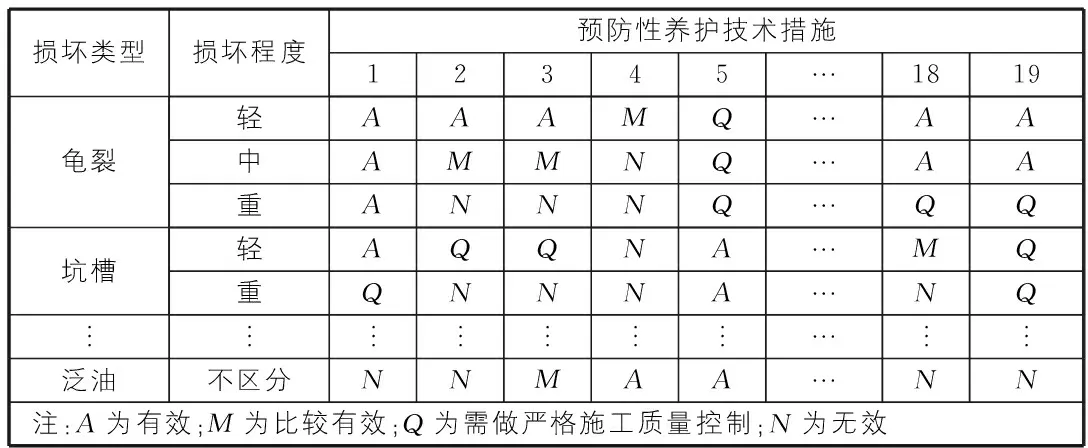
表3 高速公路沥青路面预防性养护技术措施决策矩阵

通过表3已经获得预防性养护对策的因素集，U={龟裂轻度、龟裂中度、龟裂重度、坑槽轻度、坑槽重度、…、泛油}和V={措施1、措施2、措施3、…、措施19}，同时根据工作经验获得对策效果的评价集为{A,M,Q,N}，在此基础上采用模糊数学理论构造高速公路沥青路面预防性养护措施的分析矩阵。

(3)

其中,rij为不同的损坏类型和程度在采用不同预防性养护技术措施使用效果的隶属度，成功将上述的常规决策矩阵转化为模糊分析矩阵，再与沥青路面技术状况模糊评价结果进行综合分析，获得最优化的高速公路沥青路面预防性养护技术措施[3]。基于以上研究内容，我们对锦阜高速公路某路段的路面检测项目数据进行模糊分析，最终确定了2 cm厚超薄磨耗层罩面的养护对策，经过实施预防性养护施工作业，该路段维修后各项质量指标均有大幅提高，整体服务水平有了较大的提升，充分说明养护对策选用适当。

4 结语

在对高速公路沥青路面预防性养护主要对策进行分析的基础上，基于模糊数学理论进行沥青路面技术状况模糊评价和沥青路面预防性养护对策模糊分析，建立养护对策模型，可以有效弥补现有预防性养护对策确定的不足，极大提高科学养护能力和路网服务水平。

[1] 徐 剑,黄颂昌.沥青路面预防性养护理念与技术[M].北京：人民交通出版社，2011.

[2] 王 苹.基于多层次多属性理论的公路预养护决策方法研究[D].重庆：重庆交通大学，2014.

[3] 王 阔.辽宁高速公路预防性养护维修工程应用效果总结[J].北方交通，2012(1)：1-2.

Abstract: This paper analyzes the main countermeasures for preventive maintenance of expressway asphalt pavement, based on the theory of fuzzy mathematics to evaluate the technical condition of asphalt pavement. It establishes the membership function of the evaluation indexes of the pavement technical condition. At the same time, it gives a fuzzy analysis of the preventive maintenance countermeasure. It’s of significance to determine the optimal preventive maintenance countermeasures.

Key words: fuzzy mathematics, expressway, preventive maintenance

Research on preventive maintenance of asphalt pavement based on fuzzy mathematics theory

Zhang Jiayu

(LiaoningProvinceCollegeofCommunications,Shenyang110122,China)

2016-03-17

张家宇(1974- )，男，硕士，副教授

1009-6825(2016)15-0136-02

U418

A