“虚设零点”，巧解导数的两类问题

石向阳



“虚设零点”，巧解导数的两类问题

石向阳

在高考函数压轴题中，我们经常会遇到导函数具有零点但求解相对比较繁杂甚至无法求解的问题。此时，我们不必正面强求，而是直接设出零点，充分利用其满足的关系式，谋求一种整体的转换和过渡，再结合其他条件解决问题，我们称这种解题技巧为“虚设零点”法。下面，笔者通过对一些高考题的分析，说明“虚设零点”的三大策略在解题中的作用。

一、导函数零点可求，但极值计算偏繁或无法化简的问题

这种情况，f′（x）=0一般可转化为二次方程，很容易想当然，用求根公式把零点求出来，代入极值中。但接下来要么计算偏繁，要么无法化简，复杂的算式让人无处下手，导致后继工作无法开展。正所谓“思路简单，过程烦人”，这时可以运用以下两个策略化繁为简。

策略1：反代消参，构造关于零点的单一函数。

如果问题要求解（或求证）的结论与参数无关，我们虚设零点后，一般不要用参数表示零点，而是反过来用零点表示参数，然后把极值函数变成关于零点的单一函数，再次求导就可解决相应函数的单调性、极值、最值、不等式证明等问题。

例1（2014全国高考新课标Ⅱ卷（文））已知函数f（x）=x3-3x2+x+2，曲线y=f（x）在点（0，2）处的切线与x轴交点的横坐标为-2。证明：当k＜1时，曲线y=f（x）与直线y=kx-2只有一个交点。

解：曲线y=f（x）与直线y=kx-2只有一个交点⇔g（x）=（fx）-kx+2的图像与x轴只有一个交点。g（x）=x3-3x2+（1-k）x+4，g（′x）=3x2-6x+1-k。

（1）当Δ=36-12（1-k）=24+12k≤0，即k≤-2时，g′（x）≥0，所以g（x）在上为增函数。因为g（-1）=k-1＜0，g（0）=4＞0，所以存在唯一x0∈（-1，0）使得g（x0）=0，所以g（x）的图像与x轴只有一个交点。

（2）当Δ=36-12（1-k）=24+12k＞0，即-2＜k＜1时，（x）=0有两个零点x1，x2，设x1＜x2。=1-k＞0，（1）=-2-k＜0，所以0＜x1＜1，1＜x2＜2。

当x∈（-∞，x1）时，（x）＞0，g（x）在（-∞，x1）内为增函数；当x∈（x1，x2）时，（x）＜0，g（x）在（x1，x2）内为减函数；当x∈（x2，+∞）时，（x）＞0，g（x）在（x2，+∞）内为增函数。g（x）的极小值点是x2。

所以g（x）的图像与x轴只有一个交点，只需要g（x2）＞0。由得

令x2=t，g（x2）=h（t）=-2t3+3t2+4（1＜t＜2），h′（t）=-6t2+6t=6t（1-t）＜0，故h（t）在（1，2）上为减函数，于是可得h（t）＞h（2）=0，即g（x2）＞0。所以当-2＜k＜1时，g（x）的图像与x轴只有一个交点。

综上（1）、（2）可知，当k＜1时，曲线y=f（x）与直线y=kx-2只有一个交点。

评析：本题当-2＜k＜1时，转化为证g（x2）＞0。x2是可以求出的（实际上），但我们证关于k的不等式）＞0，让人无处下手。于是，我们虚设零点x2，采用“反代”的方法，用零点x2表示参数，有这样巧妙地回避了繁杂的计算，简洁而利索，可谓妙哉。

策略2：降次留参，建立含参数的方程（或不等式）。

如果问题要求解（或求证）的结论与参数有关，虚设零点后，利用关系式f′（x）=0（大部分情况可转化为二次方程），在保留参数的情况下，不断地把零点的次数降到不可再降为止，再结合其他条件建立含参数的方程（或不等式），就可求出参数的值或参数的范围。

（1）讨论f（x）的单调性；

（2）设f（x）有两个极值点x1，x2，若过两点（x1，f（x1）），（x2，f（x2））的直线l与x轴的交点在曲线y=f（x）上，求a的值；

（3）（加编）函数f（x）的图像与x轴有三个公共点，求a的取值范围。

解：（1）略。

（2）f′（x）=x2+2x+a，由题设知，x1，x2为方程f′（x）=0的两个根，故有a＜1，x12=-2x1-a，x22=-2x2-a。因此，同理。因此直线l的方程为，设l与x轴的交点为（x0，0），得。而，由题设知，点（x0，0）在曲线y=f（x）上，故f（x0）=0，解得a=0或或。所以，所求a的值为a=0或或。

（3）函数f（x）的图像与x轴有三个公共点⇔f（x）有极大值、极小值且两个极值异号。

f（x）有极大值、极小值⇔f′（x）有两零点⇔Δ=4-4a ＞0即a＜1。

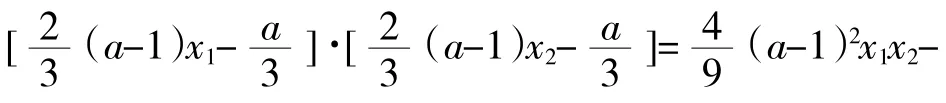
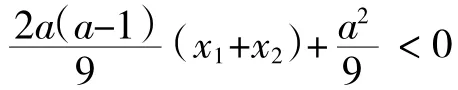
f（x）两个极值异号⇔f（x1）·f（x2）＜0，即，因为x1，x2为方程f′（x） =x2+2x+a=0的两个根，由韦达定理有x1+x2=-2，x1x2=a，代入化简得，得。

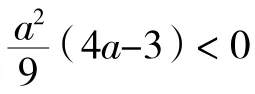
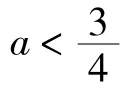
综上可知，函数f（x）的图像与x轴有三个公共点，a的取值范围为。

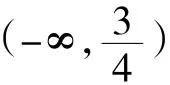
评析：对于问题（2），虚设f′（x）零点x1，x2后，找到零点x1，x2与参数a之间的联系（x12=-2x1-a，x22=-2x2-a），利用它们不断地把零点的次数降到1次为止，再利用设而不求法求出直线方程，利用直线方程求出与x轴的交点，根据交点在已知曲线上建立含参数a的方程，从而得到参数a的值；对于问题（3），等价转化为f（x1）·f（x2）＜0，再利用韦达定理转化纯粹的含参数a的不等式，求出了a的取值范围，这也要归功于问题（2）的虚设零点及降次留参。

二、导函数零点存在但无法求出的问题

如果f′（x）=0是超越形式（对字母进行了有限次初等超越运算包括无理数次乘方、指数、对数、三角、反三角等运算的解析式，称为初等超越式，简称超越式），我们无法求出导函数零点，这时一律采用“虚设零点”法，通过形式化的合理代换或推理，谋求一种整体的转换和过渡。这就是本文的第三个策略。

策略３：整体代换，将超越式化简为普通式。

例3（2015年全国高考新课标I卷（文））设函数f（x）=e2x-alnx。

（1）讨论f（x）的导函数f′（x）零点的个数；

当a＞0时，方程g（x）=a有一个根，即f′（x）存在唯一零点；

当a≤0时，方程g（x）=a没有根，即f′（x）没有零点。

（2）由（1），可设f′（x）在（0，+∞）的唯一零点为x0，当x∈（0，x0）时，f′（x）＜0；当x∈（x0，+∞）时，f′（x）＞0。故f（x）在（0，x0）单调递减，在（x0，+∞）单调递增，所以f（x）min=f（x0）。

综上所述，“虚设零点”的三大策略，让我们成功回避复杂的运算，摆脱解决问题过程中的一些技术难点，在求解比较复杂的含参函数的综合问题中具有很好的应用价值，值得我们关注。

（作者单位：长沙市南雅中学）