GPS网平差方程的自动列写及实现

洪　菊，赵　凯，李金涛，王胜利，石　波

(1.山东科技大学 测绘科学与工程学院，山东　青岛　266590；2.山东科技大学 海洋工程研究院，山东　青岛　266590)

GPS网平差方程的自动列写及实现

洪菊1，赵凯1，李金涛1，王胜利2，石波1

(1.山东科技大学 测绘科学与工程学院，山东青岛266590；2.山东科技大学 海洋工程研究院，山东青岛266590)

摘要：针对GPS网平差中由于数据过多导致的方程列写困难、运算效率低等问题，提出了GPS网平差方程自动列写及快速实现的方法。根据GPS网平差数据特点，该方法在无约束平差与约束平差具体应用过程中采用压缩存储法存储对称矩阵以节省内存空间，采用Cholesky分解法解算法方程以加快运算效率，达到GPS网平差方程的快速解算的效果。结果表明：使用该方法能够确定GPS网中点在指定参照系下的坐标，达到GB/T18314—2009对约束平差的要求；此方法与常规方法相比可较好节省内存空间，提高运算效率。

关键词：GPS网平差；无约束平差；约束平差；自动列写方程式；矩阵压缩存储；Cholesky分解法

0引言

与常规测量方法相比，全球导航系统(global positioning system，GPS)技术在精度、社会经济效益以及布网的灵活性上具有很大的优越性，因此GPS技术在测绘领域已经得到广泛的应用[1-2];但就数据处理而言，GPS观测值的数据处理与常规测量观测值的数据处理相比更加复杂。在进行GPS网平差过程中主要应用无约束平差、约束平差、联合平差3种方法，其处理流程主要是先通过无约束平差发现和剔除GPS观测值中存在的粗差以及评定网平差的精度，再进行约束平差增加约束条件，求得站点在指定坐标系下的坐标以及评定GPS网精度。GPS平差处理是GPS定位的重要组成部分，也是GPS最活跃的研究领域之一，现国内外有很多平差处理软件[3]，例如GAMZT、TopADJ、天宝Trimble Geomatics Offic等。这些软件能够处理各种网型，功能较强、操作简单。在GPS网平差中会遇到不同的平差处理问题，特别是随着站点数目的增加，实现平差方程的自动列写、自动解算和提高大量数据的处理效率变得尤为困难与重要。因此，本文针对GPS网平差数据特点，采用矩阵压缩法存储矩阵和Cholesky分解法解算法方程，实现了GPS网平差的自动列写、自动解算。

1GPS网平差的数学模型

GPS网平差模型[4-6]主要有无约束平差和约束平差两种平差模型。

1.13维无约束平差

GPS网无约束平差在只引入1个位置基准时，平差所得到的GPS网的精度指标常被作为衡量GPS网内符合精度的指标；同时通过GPS网平差所反映的观测值的质量，又被作为判断粗差观测值及其相应处理的依据。

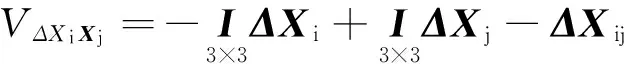
(1)

式中：

如果GPS网共有n个点，通过观测共得到m条独立基线向量，可将总的误差方程写为

(2)

引入起算基准的方法一般有2种，本文采用的方法是以GPS网中1个点的地心坐标为起算基准，即可有1个起算方程为

(3)

式中

(4)

1.23维约束平差

GPS网约束平差引入了会使GPS网的尺度和方位发生变化的外部起算数据。GPS网的约束平差常被用于确定GPS网中点在指定参照系下的坐标，主要方法有2种：第1种方法是利用已知参心坐标，计算参心系到地心系的转换关系，将已知的参心坐标系转换到地心坐标系下，然后在地心系下进行约束平差，最后将平差结果转换到参心坐标系；第2种方法是建立包含地心系到参心系下坐标参数在内的统一函数模型，平差后可直接得出待定点在参心系下的坐标。本文采用第2种方法。对于1个由n个点、m条基线向量构成的GPS网，其总的误差方程同式(2)。

一般参心坐标系下使用坐标、边长和方位作为约束条件。本文仅提供考虑坐标约束条件的基准方程，若有l个已知点坐标作为约束条件，则有约束方程

(5)

式中：

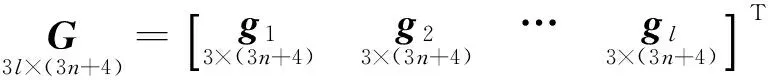
(6)

(7)

上述2种平差模型基线向量的观测值权阵，通常都是由基线解算时得出各基线向量的方差-协方差阵来确定。根据基线向量解算模式，确定最终参与计算的方差-协方差阵。针对单基线解算模式，其权阵为

P=D-1。

(8)

式中

(9)

其中dm为相应基线的方差-协方差阵。

根据式(2)、式(3)和式(5)，按照最小二乘原理进行平差计算，得到平差结果为

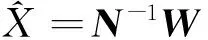
(10)

待定点坐标参数估值为

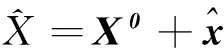
(11)

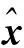
根据平差结果进行精度评定，3维无约束平差中观测值的单位权中误差为

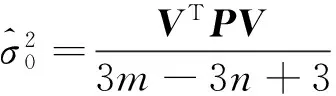
(12)

3维约束平差中观测值的单位权中误差为

(13)

2平差实现及处理方法

平差解算的流程如图1所示，首先根据基线解算结果得到站点坐标和基线向量的统计信息；然后选取作为网平差时的基线向量并利用其估值进行3维无约束网平差，根据平差结果剔除粗差，评定网精度确定最终参与无约束网平差的基线向量[7]；最后利用所确定的基线向量组成观测方程，利用已知点形成的限制条件方程进行3维约束网平差，求得待定参数的估值和观测值的平差值、观测值的改正数以及相应的精度统计信息。

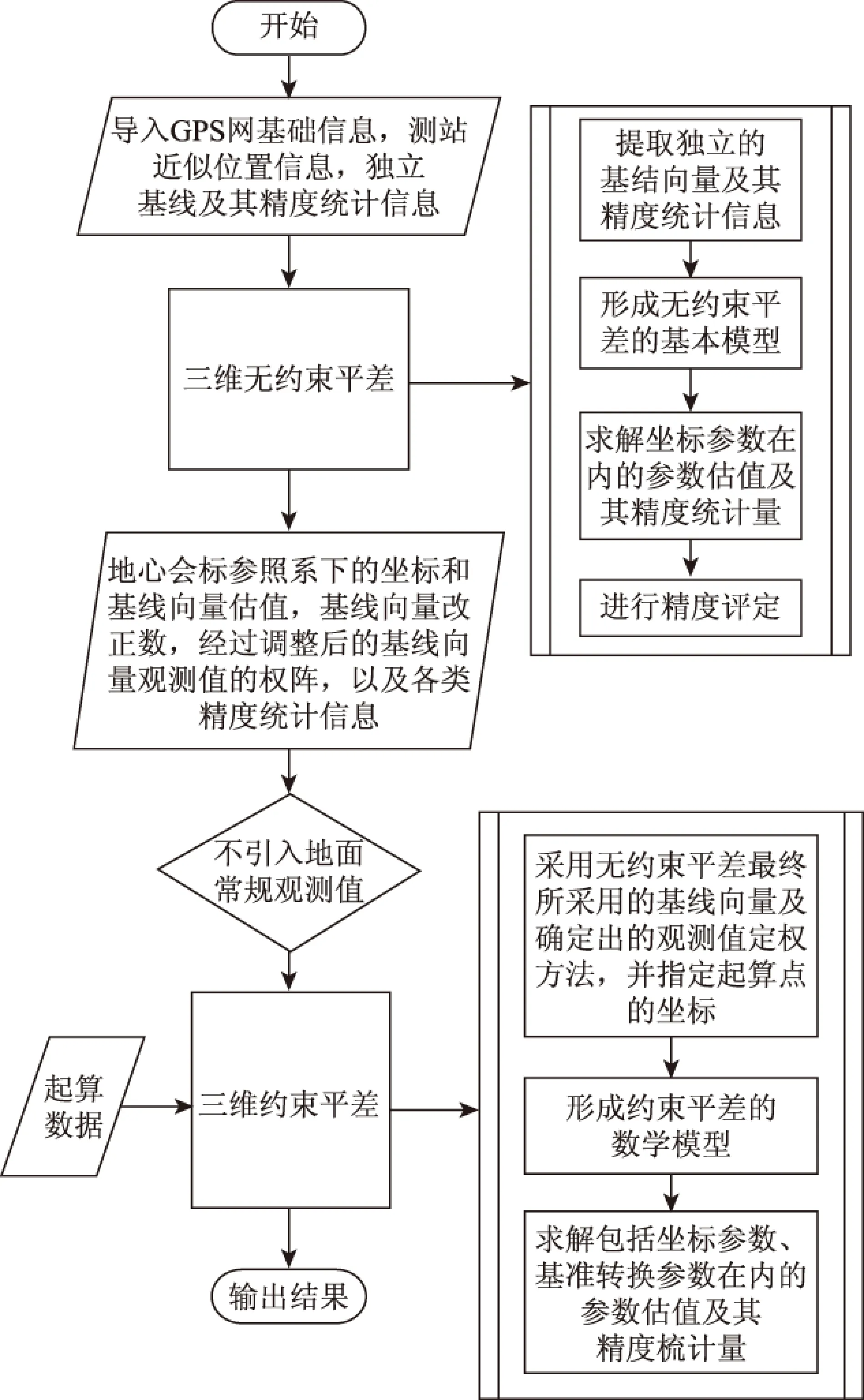
图1　平差解算流程图

本文在平差过程中使用压缩存储法与Cholesky分解法分别对矩阵和法方程进行处理，以达到节省内存空间，加快数据处理效率的结果。

2.1对称矩阵压缩存储

对称矩阵，一般只需存储上三角就可以，在实际计算中可以复现为标准的矩阵。考虑到GPS网平差中方差-协方差阵为对称正定矩阵以及误差方程系数阵分块对称的特点，使用如下存储方法，以3阶对称矩阵为例

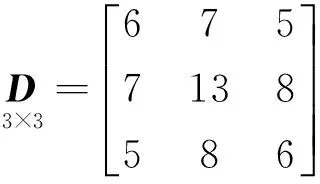
(14)

存储时，可按照向量格式存储为

(15)

此方法同规范Hadamard矩阵的压缩存储方式类似，在极限情况下，采用此种存储方法对称矩阵可节省50%的存储空间[8]。

2.2Cholesky分解法求解法方程

Cholesky分解法又叫平方根法，是求解对称正定线性方程组最常用的方法之一。基本原理为将法方程的对称正定系数矩阵分解为下三角矩阵以及它的共轭转置矩阵的乘积，这样仅通过行变换、列变换就可以解法方程。

由于法方程系数阵一般是对称正定矩阵，所以使用Cholesky分解法不用求逆就可以解法方程。

3算例分析

3.1数据概述

本实验所用数据为2011-03-31 18时至2011-03-31 18时美国CORS网7个站连续记录的导航文件和观测文件，使用HGO软件[9-10]对这7个站的数据进行处理，得到了这个时间段7个测站的站坐标文件以及基线向量文件，测区如图2所示，本测区位于美国旧金山附近，使用源坐标WGS84，使用源椭球WGS84，无椭球转换参数。

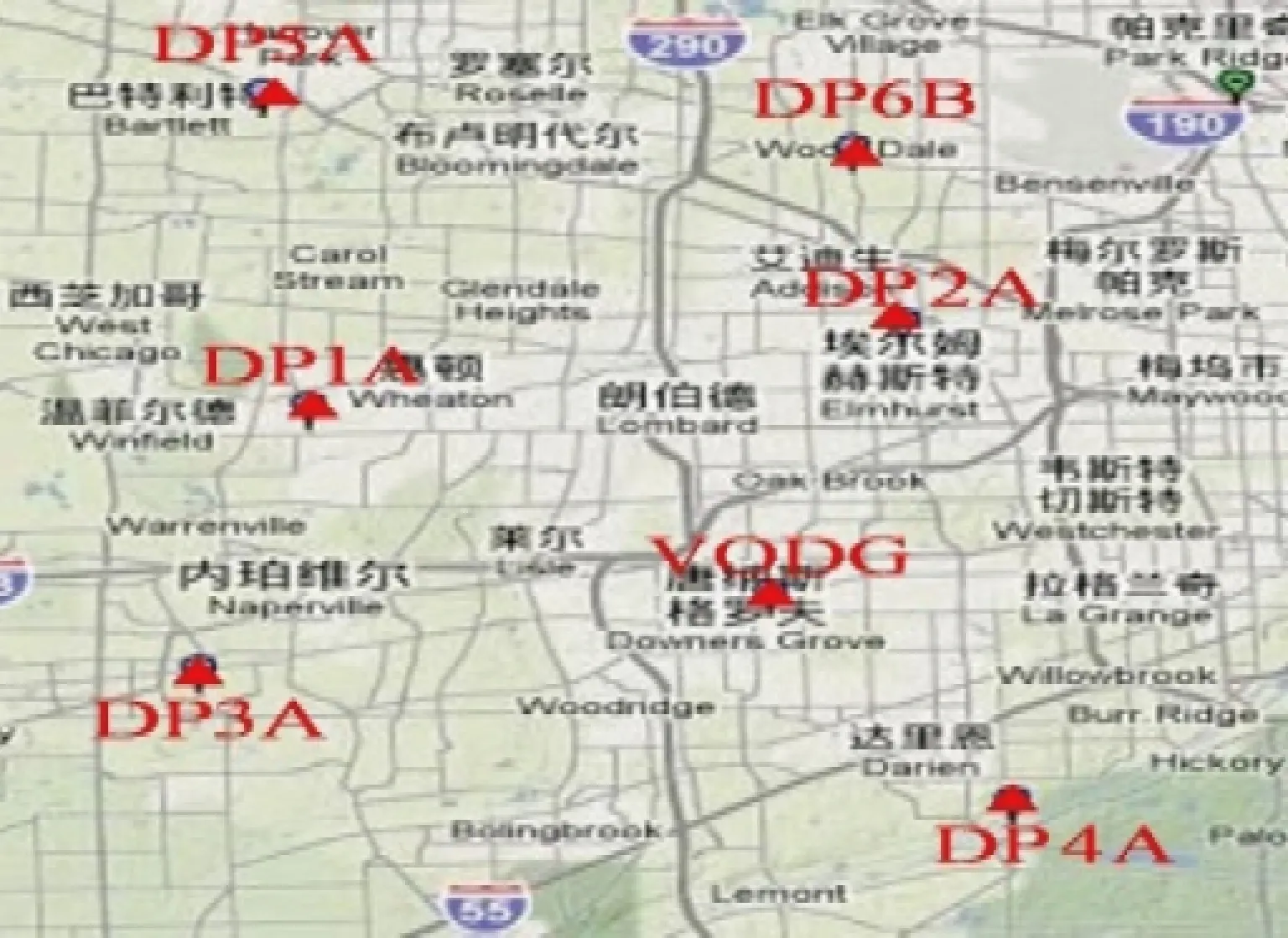
图2　实验测试测区示意图

3.2方法分析

1)在GPS网平差中，由于数据量较大，占用大量内存空间使得计算效率低，同时考虑到方差-协方差阵对称和误差方程系数阵分块对称的特点，本文采用的矩阵压缩存储法与常规矩阵存储方法相比，节省了内存空间，提高了运算效率。

本实验无约束网平差中系数阵是对角线元素全为-1的单位阵，只需要存储对角线数值，约束网平差中将系数阵作为分块对称矩阵进行存储，方差-协方差阵全部压缩存储，压缩存储前后数据占用内存单元见表1。

表1　压缩存储结果分析表

2)GPS网平差中一般使用求逆法与LU分解法求解法方程。求逆法不仅效率低，而且当数据量过大时会导致求逆结果不稳定；LU分解法是将系数矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积，直接通过行变换与列变换就可以直接解法方程，克服了求逆法的缺点。但考虑到GPS网平差中法方程系数阵对称正定的特点，本文采用Cholesky分解法只需要将法方程系数矩阵分解为下三角矩阵以及它的共轭转置矩阵的乘积，这种方法较普通的LU分解差不多快一倍[11]。

本实验在无约束网平差与约束网平差求解法方程中均采用了Cholesky分解法进行解算，提高了解算速度。

3.3结果分析

在3维无约束平差中以点DP1A坐标为起算数据，平差后得到21条基线向量的信息。由于数据过多，本文只选取其中7条基线向量的改正数及中误差等信息，如表2所示。

表2　3维无约束平差后基线向量改正数及中误差等信息分析表

根据GB/T18314—2009的要求，对21条基线进行残差检验，结果如图3所示。

图3　无约束平差残差分析图

图3中横坐标代表参与无约束平差的基线向量个数。由图3可知，无约束平差基线向量改正数的绝对值满足要求

(16)

由式(16)可知21条基线向量可全部用于约束平差。

约束平差中引入点DP1A、DP2A、DP3A 3点的坐标为约束条件，约束平差后得到21条基线向量的信息；由于数据过多，同样只选取其中7条基线向量的改正数及中误差等信息，如表3所示。

表3　3维约束平差后基线向量改正数及中误差等信息分析表

根据GB/T18314—2009要求，对21条基线进行残差检验，结果如图4所示。

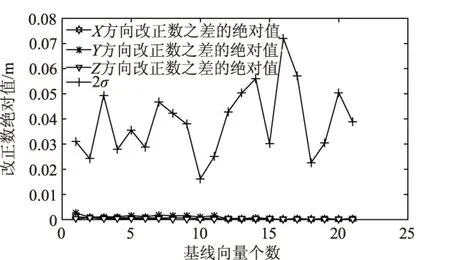
图4　约束平差残差分析图

图4中横坐标代表参与约束平差的基线向量个数。约束平差中，基线分量改正数经过粗差剔除后的无约束平差的同一基线相应改正数较差的绝对值满足要求

(17)

式(17)证明作为约束的已知点坐标不存在误差较大的值。

4结束语

本文针对GPS网平差数据的特点进行了解算方式的改进，实现了同步环的自动构建并完成了网平差，评定了观测值精度，达到了压缩内存、快速解算的效果；但是在规模较大、系统误差复杂的GPS网整体平差中仍然有许多问题需要研究，例如观测量的选取，网形的构建等都值得进一步探究。

参考文献

[1]曹鸽，王玉柱.GPS、RTK、网络RTK技术在工程测量中的应用[J].北京测绘，2012(5)：83-85.

[2]令狐义强.GPS-RTK技术在城市地籍测量中的应用[J].测绘与空间地理信息，2011，34(3)：108-110.

[3]张辛，许其凤，杨爱明，等.GPS数据处理软件的功能与性能分析[J].测绘科学技术学报，2014，31(4)：347-350.

[4]徐绍铨，张华海，杨志强，等.GPS测量原理与应用[M].3版.武汉：武汉大学出版社，2008：162-166.

[5]王忠礼，顾刘丹，姬前锋.MATLAB软件支持下的GPS基线向量网的3维无约束平差[J].北京测绘，2014(1)：80-80.

[6]王忠礼，顾刘丹.MATLAB软件支持下的GPS基线向量网3维约束平差[J].全球定位系统，2014，39(6)：32-36.

[7]高丽峰，唐卫明，冯彦同，等.GPS长基线数据处理方法分析[J].测绘信息与工程，2012，37(2)：13-15.

[8]姚鹏，龚威.Hadamard矩阵压缩存储算法分析与研究[J].微型机与应用，2013，32(19)：82-84.

[9]广州中海达定位技术有限公司.HGO数据处理软件包(中文版1.0.11)[EB/OL].(2013-12-18)[2015-12-26].http：//www.zhdbds.com/A/?C-1-92.Html.

[10]周正朝，袁本银，潘国富.中海达HGO软件在GPS/BDS/GLONASS静态解算的应用分析[J].测绘通报，2013(3)：120-121.

[11]PRESS W H，TEUKOLSKY S A，VETTERLING W T，et al.C数值算法[J].傅祖芸，赵娜娜，丁岩石，译.2版.北京：电子工业出版社，2004：96-97.

Automatic establishment and realization of GPS net adjustment equation

HONG Ju1，ZHAO Kai1，LI Jintao1，WANG Shengli2，SHI Bo1

(1.College of Geomatics，Shandong University of Science and Technology，Shandong Qingdao 266590，China；2.Institute of Ocean Engineering，Shandong University of Science and Technology，Shandong Qingdao 266590，China)

Abstract：In view of the difficulty of writing and the low computation efficiency of the equation caused by large amounts of data in GPS network adjustment，a method of the automatic establishment and quick realization of GPS net adjustment equation was presented in this paper.In the light of the characteristics of GPS net adjustment data，in order to save memory space and improve computation efficiency，the compression storage method and the Cholesky decomposition method were taken to store positive definite matrices and resolve normal equations in the specific applications of free adjustment and constraint adjustment.The result showed that the method compared with the conventional one could save memory space and improve computation efficiency greatly on the basis of rightly determining the coordinate of the midpoints of GPS network in the specified reference coordinate system,with matching the accuracy requirements of GB/T18314—2009 for constraint adjustment.

Keywords：adjustment of GPS network；free adjustment；constraint adjustment；automatic established equation；matrix compression storage；Cholesky decomposition method

收稿日期：2016-01-20

基金项目：海岛(礁)测绘技术国家测绘地理信息局重点实验室资助项目(2014B02，2015A01)。

第一作者简介：洪菊(1994—)，女，山东济南人，本科学历，研究方向为GNSS数据处理。

中图分类号：P228

文献标志码：A

文章编号：2095-4999(2016)02-0108-05

引文格式：洪菊，赵凯，李金涛，等.GPS网平差方程的自动列写及实现[J].导航定位学报，2016，4(2)：108-112.(HONG Ju，ZHAO Kai，LI Jintao，et al.Automatic establishment and realization of GPS net adjustment equation[J].Journal of Navigation and Positioning，2016，4(2)：108-112.)DOI：10.16547/j.cnki.10-1096.20160223.