卫星导航定位系统中监测站URE解算研究

张京宁，闫建华，崔　煜

(1.北京卫星导航中心，北京　100094；2.61320部队，西安　710038)

卫星导航定位系统中监测站URE解算研究

张京宁1，闫建华1，崔煜2

(1.北京卫星导航中心，北京100094；2.61320部队，西安710038)

摘要：针对监测站接收数据有限的问题，提出一种利用有限数据计算用户距离误差(URE)的方法：首先分别利用Klobuchar模型和Hopfield模型对接收机的观测伪距进行电离层和对流层修正，在此基础上进行卫星钟差和接收机钟差改正；最后利用多普勒观测值进行地球自转效应和相对论效应修正，得到修正之后的伪距。通过4台监测接收机的修正伪距，利用最小二乘法对卫星定位，计算出卫星在地心地固坐标系中的坐标，与直接利用广播星历计算出来的坐标在RTN坐标系中进行比对，最终计算出URE。结果表明该方法对监测站的数据后处理有一定的参考作用。

关键词：URE；多普勒；坐标系；导航；监测站

0引言

在卫星导航定位中，对定位结果产生影响的因素很多，用户距离误差(user range error，URE)是误差源对伪距测量的综合影响所产生的整体误差，反映了用户能够获得的定位精度，是评价卫星导航定位系统性能的关键指标，与系统地面控制部分和空间星座部分密切相关[1]。URE的解算需要用到卫星导航电文和监测站原始观测数据；因此监测站进行URE解算对检测卫星完好性、导航电文正确性、伪距合理性等都有辅助作用。但由于监测站数据来源有限，URE解算受到一定的限制，因此在具体解算过程中，需要一种利用有限数据计算URE的方法。

URE的解算过程是先由监测站接收的广播星历推算出特定时刻卫星的位置，然后根据监测接收机实际接收伪距值消除掉电离层和对流层延迟、卫星和监测接收机钟差、地球自转、相对论等带来的影响，通过3台监测接收机和修正之后的伪距值，解算出卫星在该时刻的真实位置。卫星轨道坐标系(RTN)的定义为：坐标原点在卫星质心；R轴为径向，与地心到卫星质心的向径方向一致；T为横向，在轨道面内与R轴垂直，并指向卫星运动方向；N轴为轨道面正法向，与R、T轴成右手系。将所得到的2个位置坐标在RTN坐标系下进行比对，得到在3个坐标方向上的分量，从而计算出URE[2]。

1卫星理论位置计算

以全球定位系统(global positioning system，GPS)星历格式为例，利用基本法在地心地固坐标系(Earth-centered Earth-fixed，ECEF)下计算卫星理论位置。表1给出了GPS广播星历参数的定义[3]。

表1　GPS广播星历

(1)

2监测站伪距修正考虑因素

由于监测站接收卫星观测数据是原始伪距，因此通过观测数据进行卫星实际位置解算时，要对原始伪距进行多项修正，把对伪距真值产生影响的因素从观测伪距中扣除。在解算过程中，需要考虑的修正因素有对流层和电离层延迟、地球自转和相对论效应、卫星和接收机钟差[4]。

2.1电离层对流层改正

监测站接收机处理软件中生成的.JG文件中包含有对流层和电离层修正结果数据，监测站对流层改正采用的是Saastamoinen模型+Neil投影函数，电离层改正采用的是Klobuchar模型[5]。本文以Klobuchar模型为例介绍改正数的计算方法。该模型修正过程为首先求得接收机与卫星连线和电离层交点处垂直方向的延迟量，再乘以用高度角求得的倾斜因子，从而得到各个卫星的延迟改正量[6]。Klobuchar模型采用采用三角余弦函数的形式，其数学表达式为

(2)

式中：Tz(t)为是垂直方向延迟(单位为 s)；t为接收机至卫星连线与电离层交点处的地方时；5×10-9为夜间值的垂直延迟常数；14h对应于余弦曲线极点的地方时，一般取为 50 400 s(即当地时间为 14：00：00)。

A为白天余弦曲线的幅度，由广播星历中的系数αn求得

(3)

为避免αn有误导致大气延迟改正和伪距改正值错误，在实际计算中一般通过高阶插值方法验证和估算αn， 确保该值准确。

P为余弦曲线的周期，根据广播星历中的系数βn求得，βn的准确性同样可以利用插值方法验证和估算为

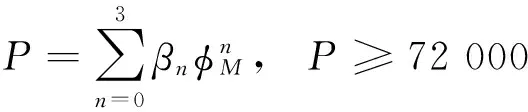
(4)

式中φM为穿刺点M的磁纬(单位为半圆对应的弧度π，例如磁纬为90°，则φM的数值为0.5(便于公式计算，下同)。

φM=φi+0.064cos(λi-1.617)。

(5)

式中φi和λi分别是M点处的大地纬度(量值为π)和大地经度(单位为rad)。

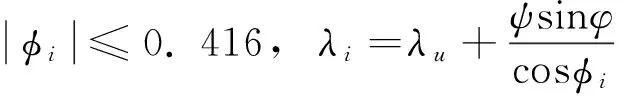
(6)

式中：λu为接收机处的大地经度(量值为π)；φu为接收机处大地纬度(量值为π)；ψ为接收机和M两点的地心夹角(量值为π)；φ为卫星的方位角(单位为rad)；且

倾斜因子I=1.0+16.0×(0.53-H)3， 因此电离层改正数为

T(t)=ITz(t)。

(7)

2.2钟差修正

卫星钟差是引起定位误差的重要因素之一，对卫星钟差的修正采用

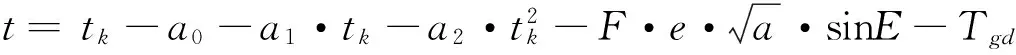
(8)

式中：E为卫星高度角；tk为瞬时历元到参考历元的时间差tk=t-toe；ai(i=0,1,2)和Tgd为广播星历中的卫星钟差修正参数[7]。

接收机钟差随历元变化，但本文中因接收机数据有限，可以通过数据统计得出钟差均值，并且该值主要受接收机硬件和线缆连接情况等不变因素影响;因此在引用计算过程中可以近似看作是固定值。

2.3地球自转和相对论修正

地球自转的影响主要表现在卫星与监测接收机的径向距离的变化上，相对论效应主要表现在接收机接收频率的变化，这2方面可用多普勒观测值近似修正[8]，反映到伪距上为

Δρ=λDP。

(9)

3计算卫星实际坐标值

通过监测站3台监测接收机和修正之后的伪距，就可以求出卫星在某一时刻的实际位置(x1，y1，z1)。 假设3台监测接收机的坐标分别为(x1，y1，z1)， (x2，y2，z2)， (x3，y3，z3)， 在时刻t接收到G1星的伪距经过修正之后为(L1，L2，L3)， 伪距观测方程为

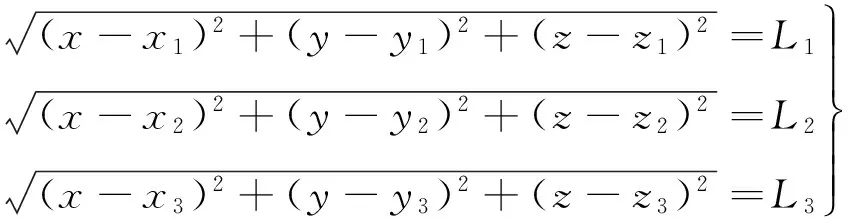
(10)

利用泰勒级数将式(10)展开为

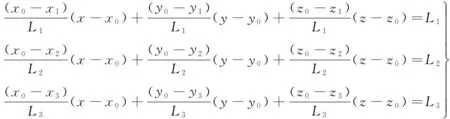
(11)

改写成矩阵形式为

AΔX=L。

(12)

式(12)中：

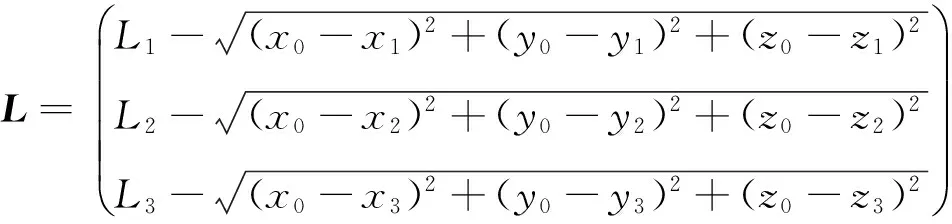
从而求出ΔX=A-1L。 以相邻2次运算的伪距差作为迭代的条件，当其小于某一固定值时，令迭代终止，从而得出卫星的实际位置[9]。

2.4误差求解

坐标系转换是将坐标系由2000国家大地坐标系(China geodetic coordinate system2000，CGCS2000)转换到RTN坐标系下，转换过程如下：

1)原点平移由大地原点平移到卫星原始轨道位置，即

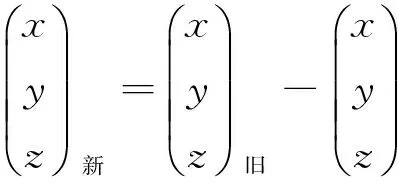
(13)

2)固定X轴旋转Z轴，即

(14)

3)固定Z轴旋转X轴，即

(15)

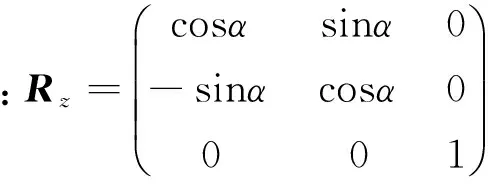
求得2卫星在RTN坐标系下的坐标分别为(X1，Y1，Z1)新、 (X2，Y2，Z2)新， 求得2个坐标值之间的差值为：

σR=X2新-X1新；σT=Y2新-Y1新；σN=Z2新-Z1新。

(16)

计算卫星URE时，主要考虑最大可视范围和用户有仰角限制的情况，因此引入加权平均思想:一方面卫星轨道值在R方向精度要远好于T、N方向，这是考虑加权的主要因素；另一方面不同高度轨道的卫星计算精度不同，所以在计算整个星座URE时，也需要引入加权系数[10]。根据推算求得的用户距离误差较为准确，在数据量有限的情况下，在监测站范围内的适用性比较好,公式为

(17)

4结束语

URE通常作为导航星座的用户伪距精度的一个重要指标，被用来评判导航星座定位性能。本文给出监测站数据受限情况下计算URE的方法，不但考虑轨道径向、迹向、法向的精度，还顾及到不同轨道精度；通过加权，改善原有方法，能够更好地反映监测站用户测距误差：在监测站数据量有限的情况下，本方法在数据后处理方面具有一定借鉴意义。

参考文献

[1]谭述森.卫星导航定位工程[M].北京：国防工业出版社，2010：245-246.

[2]贾蕊溪，董绪荣，尚晨，等.北斗卫星导航系统URE与定位精度分析[J].现代电子技术，2014，37(17)：26-28.

[3]刘磊，盛峥，王迎强，等.利用广播星历计算GPS卫星位置及误差分析[J].解放军理工大学学报：自然科学类，2006，7(6)：592-596.

[4]李征航，屈小川.全球定位系统的新进展(讲座) 第1讲 导航电文结构的变化和参数的精化——从导航电文的变化看GPS的进展[J].测绘信息与工程，2012，37(1)：49-54.

[5]李飞，段哲民，龚诚，等.GNSS接收机自主完好性监测算法研究[J].测绘通报，2007(8)：14-15.

[6]罗鸣，曹冲，肖雄兵，等.全球定位系统[M].北京：电子工业出版社，2008：136-137.

[7]焦月，寇艳红.GPS卫星钟差分析、建模及仿真[J].中国科学：物理学 力学 天文学，2011，41(5)：596-601.

[8]查明.顾及地球引力摄动的卫星和卫星星下点位置计算[J].测绘科学与工程，2006，26(1)：44-46.

[9]范媚君，周建华，牛飞，等.卫星导航系统基本完好性算法及性能分析[J].测绘科学技术学报，2011，28(6)：407-415.

[10]苏天祥，文援兰，符京杨.关于导航星座URE计算方法的讨论[J].测绘科学，2014，39(11)：3-5.

Research of calculating station URE of satellite navigation system

ZHANG Jingning1，YAN Jianhua1，CUI Yu2

(1.Beijing Satellite Navigation Center，Beijing 100094，China；2.Troops 61320，Xi’an 710038，China)

Abstract：Based on limited receiving data，the article preposed a URE calculating method.It first revised the ionosphere and troposphere of pseudo-range using Klobuchar and Hopfield model，and revised satelliting clock bias and receiving clock bias，then getting correct pseudo-range after revising the Earth’s rotation and relativism.By calculating the satellite coordinates in geocentric axes using least square method，compared with the coordinates in RNT system，finally it got the URE.The result showed this method could provide a reference for data after treatment.

Keywords：user range error；Doppler；coordinate system；navigation；monitoring station

收稿日期：2015-07-09

第一作者简介：张京宁(1979—)，女，北京人，工程师，研究方向为卫星导航定位算法。

中图分类号：P228.1

文献标志码：A

文章编号：2095-4999(2016)02-0098-04

引文格式：张京宁，闫建华，崔煜.卫星导航定位系统中监测站URE解算研究[J].导航定位学报，2016，4(2)：98-101.(ZHANG Jingning，YAN Jianhua，CUI Yu.Research of calculating station URE of satellite navigation system[J].Journal of Navigation and Positioning，2016，4(2)：98-101.)DOI：10.16547/j.cnki.10-1096.20160221.