基于克里金插值法的NRTK误差改正

石　鑫，吕志伟，杨　川，张　宇

(1.信息工程大学 导航与空天目标工程学院，郑州　450001；2.核工业西南勘察设计研究院有限公司，成都　610061)

基于克里金插值法的NRTK误差改正

石鑫1，吕志伟1，杨川2，张宇1

(1.信息工程大学 导航与空天目标工程学院，郑州450001；2.核工业西南勘察设计研究院有限公司，成都610061)

摘要：针对NRTK中流动站误差修正时，传统内插模型改正精度不高的问题，提出用克里金插值法对流动站误差进行建模估计，并阐述方法的数学过程。结果表明，克里金插值法能够有效改正用户电离层、对流层延迟，改正精度较常规内插方法有所提高:当用户位于基站网络内部时，克里金插值法的电离层和对流层改正精度与常规内插算法相当；用户位于网外时，常规内插方法难以有效改正用户大气延迟，而克里金插值法在网外一定范围内仍能有效改正电离层、对流层延迟。

关键词：克里金；NRTK；电离层延迟；对流层延迟；误差改正

0引言

在全球范围内，面向cm级高精度实时动态定位服务的多功能连续运行参考站系统相继建立，并成为重要的地理空间数据基础设施[1-2]，其数据处理核心包括3个方面：参考站网络模糊度解算技术、流动站误差建模、改正数发布，这些技术让网络实时动态差分法(network real-time kinematic，NRTK)实现了中长距离的高精度实时动态定位。其中流动站误差建模是为了对用户位置处的空间相关误差进行改正，数据处理中心依据各参考站的空间相关误差建模估计流动站用户的空间相关误差并将其播发给流动站用户，主要是电离层、对流层延迟信息;流动站接收机依据数据处理中心播发的信息改正自己的大气延迟，改正结果直接影响用户的定位精度，当改正精度较低时，可能导致用户在一段时间内无法获得固定解。参考站网络模糊度解算完毕后，就可以利用基站的大气延迟信息对流动站大气延迟进行误差建模，常规的模型有线性组合法(linear combination model，LCM)、线性内插法(linear interpolation method，LIM)、基于距离线性内插法(distance based linear interpolation method，DIM)、低次曲面模型法(low-order surface model，LSM)、最小二乘配置法(least-squares collocation，LSC)等[3-4]，这些方法均能一定程度上改正用户的大气延迟。分类建模和模型精化是NRTK误差建模领域的最新趋势[5]，文献[6]对现有的内插方法进行了分析，结果表明：现有各种内插算法在电离层改正精度上大体相同，但在对流层等误差的改正方面，各种模型均有所不足。文献[7]系统性地研究分析了评价各种插值算法精度的方法，使针对内插算法的精度评定更合理、更符合实际情况。近几年，国内外一些学者将克里金(Kriging)插值法引入全球卫星导航系统(global navigation satellite system，GNSS)数据处理中来。文献[8]中的研究表明：Kriging插值法能够顾及对流层和电离层在空间和时间上的变化；能较准确地对区域电离层、对流层建模。文献[9]将Kriging插值用于实时动态定位中:在使用广播星历的情况下获得了cm级的定位精度；说明了Kriging插值法用于区域大气误差建模的可行性。文献[10]用Kriging插值法构建了中纬度区域的电离层总电子含量(total electron content，TEC)地图，并证明了Kriging插值法能够很好地表现TEC的分布情况。

本文基于大型连续运行参考站(continuously operating reference stations，CORS)网的全球定位系统(global positioning system，GPS)观测数据，利用Kriging插值法实时估计流动站用户的大气延迟改正；并将所得结果与常规内插方法结果对比，以评估Kriging插值法在多参考站NRTK中的适用性及其优劣性。

1参考站网络大气延迟信息的提取

大气误差的分类建模已成为NRTK中误差改正的主要模式。分类建模一方面顾及了不同误差源之间不同的空间相关特性，使误差改正更具针对性，提高了改正效果；另一方面避免了误差源之间的相互影响从而拉低整体的改正精度。在提取参考站网络大气延迟信息时，可先根据解算出的双差网络模糊度求得网络基线上的双差电离层延迟，然后根据双差相位观测方程求得各网络基线的双差对流层延迟。

现阶段参考站通常选用多频接收机和多路径抑制天线，有效降低了接收机噪声对载波相位的影响，使其保持在5 mm内；同时高阶电离层延迟误差影响远小于一阶影响的0.1%，对200 km以下的基线而言，其差分项影响不大于5 mm[5]。参考站网络模糊度解算完毕后，利用双频相位观测值，忽略观测噪声和高阶电离层延迟的影响，可计算参考站网络基线上L1载波的一阶双差电离层延迟[5，11]为

Δφ1-λ2Δφ2)+

(λ1ΔN1-λ2ΔN2)]。

(1)

式中：f1、 f2为L1、L2频率；λ1、 λ2为L1、L2波长；Δφ1、Δφ2为双差载波相位观测值；ΔN1、ΔN2为双差整周模糊度。

双差电离层延迟提取完毕后，可根据双差相位观测方程求得基线上双差对流层延迟信息为

ΔT=λ1(Δφ1+ΔN1)-Δρ+ΔI-ΔO。

(2)

若采用精密星历进行数据处理，则卫星轨道误差可忽略不计，将式(1)代入式(2)中，可求得参考站网络基线的双差对流层延迟计算公式为

(3)

需要指出的是：为使求得的参考站网大气延迟信息真实可靠，选用参考站网络模糊度固定的时段进行解算，排除因模糊度未固定对下一步用户大气延迟建模的影响；由于实时定位的需要，要求每个历元都要对用户大气延迟进行建模改正，因此选用的时段除了要求参考站网模糊度固定外，还应保持时间的连续性。

2普通Kriging插值法对用户大气延迟的建模实现

Kriging插值法是最早由南非矿业工程师Krige提出的一种空间自协方差最佳插值法，在地下水模拟、土壤制图、地质统计等方面得到了广泛应用，可对研究对象提供一种最优线性无偏估计。普通Kriging插值法既可对点进行估计，也可对块或区域属性进行估计[12]。相对于NRTK中常用的其他几种内插方法，Kriging插值法考虑了样本数据在空间和时间上的相互关系，并以半方差的形式来体现[13]；同时和常规数学内插方法不同的是，Kriging插值法以克里金方差来对插值结果进行衡量。普通Kriging插值法关键步骤是求各样本数据的权重，求出权重后即可对待估点进行估计，普通Kriging插值法的基本原理[14]为

(4)

式中：Z(xi)为样本点属性值;λi为系数。为实现最优线性无偏估计，必须满足无偏估计和估计方差最小的2个条件，最终体现为

(5)

式中：γ(xi，xj)为2个样本点之间的半方差；φ为最小化方差时的拉格朗日乘数。

Kriging插值法用于NRTK大气误差建模时，将各参考站视为样本点，参考站上的大气延迟信息(电离层、对流层)视为样本点的属性值。普通Kriging插值法对用户大气延迟进行实时建模估计大致可分为以下4个步骤：

1)实时解算参考站网络基线模糊度，并按式(1)、式(3)求取相关基线的双差对流层延迟、双差电离层延迟，并根据参考站网络基线的双差对流层、双差电离层延迟计算半变异函数值为

(6)

式中：(xi，yi)、(xj，yj)为2个参考站的平面坐标；h为参考站之间的距离；N为距离为h的参考站对数；Z(xi，yi)、Z(xi，yi)为(xi，yi)、(xj，yj) 2点上相应的对流层延迟或电离层延迟。

2)选择合适的变异函数，常用的变异函数有线性模型、球状模型、指数模型、高斯模型、幂函数模型、对数函数模型、空穴效应模型几种。根据文献[9-10]，高斯模型和指数模型比较适用于GNSS大气延迟的建模估计，能够较好地反映区域大气延迟的空间相关性，它们的函数模型[15]为：

指数模型

(7)

高斯模型

(8)

变异函数选好后，根据第一步求得的半变异函数值来拟合变异函数中的参数c0、c1、a， 然后计算用户与各参考站之间的变异值为

(9)

式中：n为参考站编号；u为用户标识。

3)根据式(5)建立方程组，求解各参考站的Kriging插值权重为

x=A-1·b。

(10)

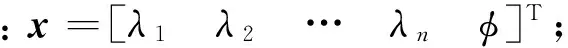
4)利用参考站基线双差对流层延迟、双差电离层延迟及各参考站相应的Kriging插值权重求用户与主参考站间的双差大气延迟为

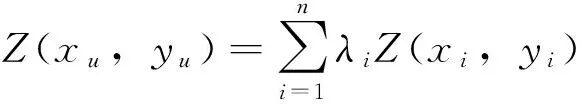
(11)

式(4)～式(11)即为用Kriging插值法对参考站网络大气延迟信息建模并估计流动站用户大气延迟的主要步骤，其中第二步的变异函数有多种模型可供选择，包括线性模型、球状模型、指数模型、高斯模型、幂函数模型、对数函数模型等；但只有指数模型、高斯模型、球状模型较适用于大气误差的建模[10]，其他几种模型的效果较差。

3实验与结果分析

为有效评估Kriging插值法对用户大气延迟的的改正精度，将其插值结果与现阶段广泛运用的LIM、LCM、LSM 3种内插算法进行对比。实验采用天津某CORS网中12个参考站(见图1)的观测数据，参考站间距为26.4 ～78.1 km不等，选取某日早上9—12时3 h的观测数据，采样间隔为1 s。对电离层进行建模估计时，Kriging插值法高斯模型改正精度略高于指数模型，而指数模型在对流层估计时改正效果优于高斯模型;因此，本文在构建Kriging插值法模型时，不再对变异函数的优劣进行探讨，电离层估计时直接选用高斯模型，对流层估计选用指数模型。实验时，选择一个基站作为流动站，并估计各网络基线的双差模糊度；然后计算基线上的双差电离层、对流层延迟，并以此作为标准值，用Kriging、LIM、LCM、LSM对流动站处双差电离层、对流层延迟进行建模估计，将其结果与标准值进行对照。为充分探讨Kriging插值法在大型NRTK中的适用性，分别设计了网内建模估计和网外建模估计2个实验，即流动站位于CORS网内和网外2种情况。

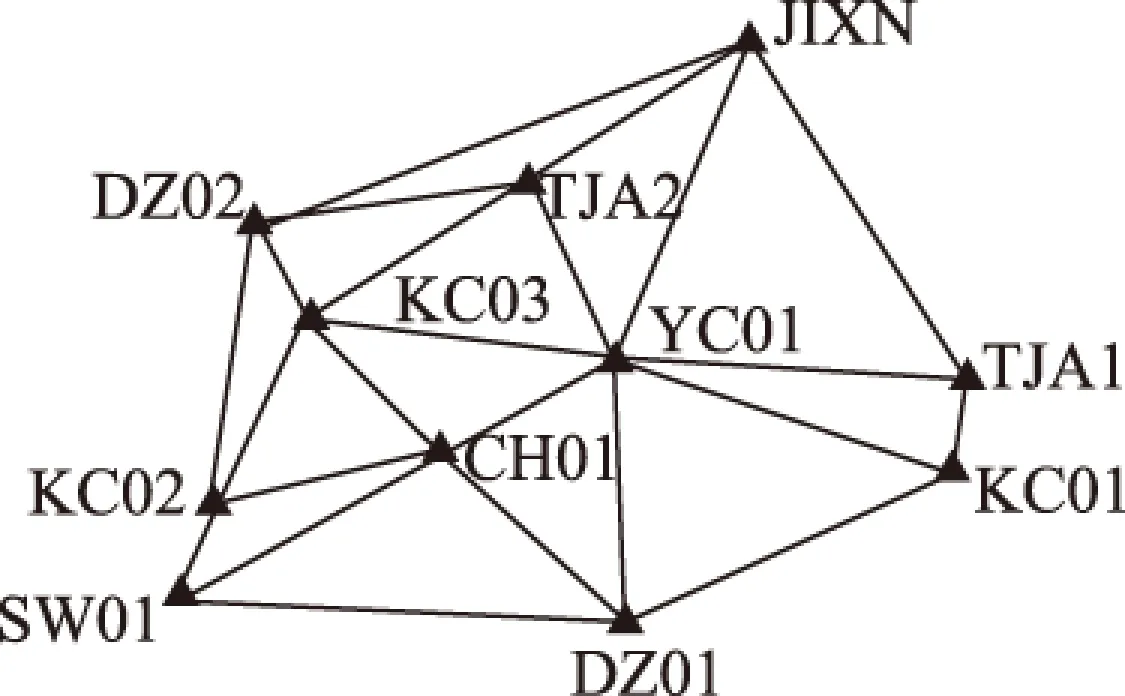
图1　基站分布图

实验一：以YC01为主参考站、CH01为流动站，用YC01-JIXN、YC01-TJA2、YC01-DZ02、YC01-KC02等其余基线的双差电离层、对流层延迟来估计YC01-CH01基线的双差电离层、对流层延迟，以此来模拟用户位于网内的情况；选取8号卫星L1载波各基线的双差大气延迟进行实验，以基线解算时估计的双差电离层、对流层延迟为真值，将Kriging插值结果与真值进行对比，实验结果如图2、图3所示。

图2　Kriging插值法估计的双差电离层延迟(网内)与标准值的比较

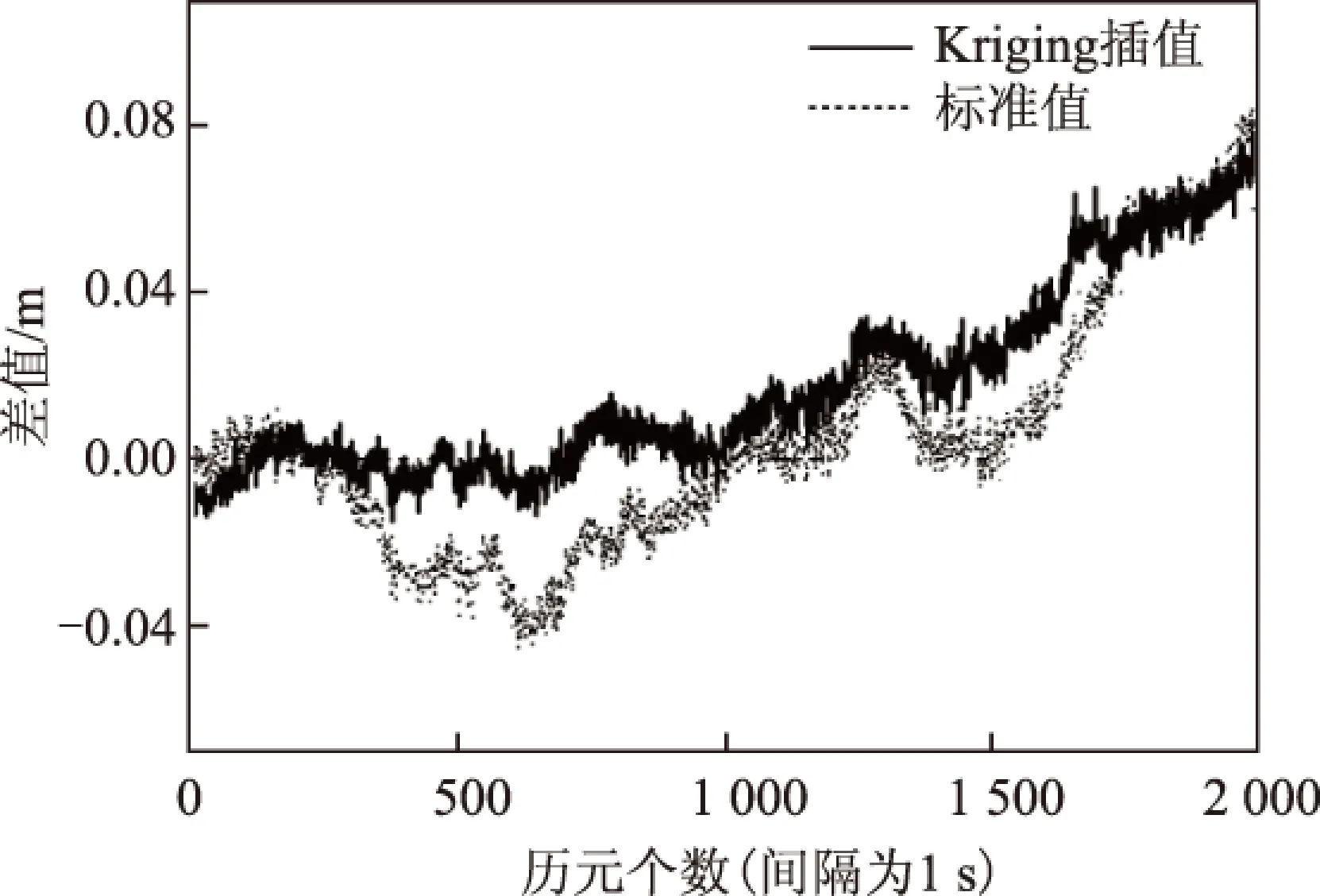
图3　Kriging插值法估计的双差对流层延迟(网内)与标准值的比较

实验二：以YC01为主参考站、DZ02为流动站，距参考站网20.3 km，用YC01-JIXN、YC01-TJA2、YC01-DZ01、YC01-KC02等其余基线的双差电离层、对流层延迟来估计YC01-DZ02基线的双差电离层、对流层延迟，以此模拟用户位于网外的情况；同样采用8号卫星L1载波各基线的双差大气延迟为实验数据，实验结果如图4、图5所示。

图4　Kriging插值法估计的双差电离层延迟(网外)与标准值的比较

图5　Kriging插值法估计的双差对流层延迟(网外)与标准值的比较

为充分探讨Kriging插值法对大气延迟的改正效果，将Kriging插值法的结果与标准值作差，统计其对双差电离层、对流层的改正精度；同时统计LCM、LSM 3种常用内插算法的改正精度，结果对比如表1和表2所示。表中In表示流动站位于网内的情况，Out表示流动站位于网外的情况。图6、图7为3种插值法的精度对比情况。

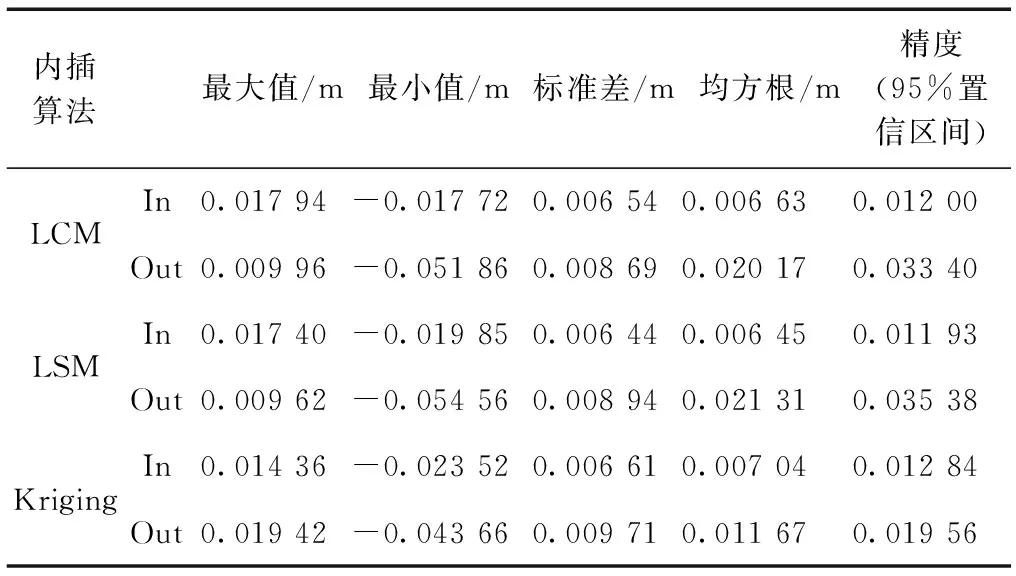
表1　电离层改正精度统计

表2　对流层改正精度统计

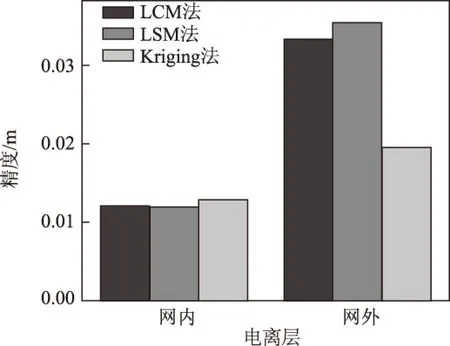
图6　电离层建模精度对比

图7　对流层建模精度对比

从图2～图5可以看出，Kriging插值法能够有效估计流动站双差大气延迟，满足大型NRTK的应用需求。在电离层估计方面，无论在网内还是网外一定范围内，Kriging插值法都能较准确地估计流动站电离层延迟，且与理论值符合较好，插值精度维持在2 cm内；对流层估计方面，在网内时，Kriging插值法的估计精度较稳定地维持在4 cm内，在网外一定范围时，插值精度虽然有所下降，但是在95%的置信区间下，仍能达到7 cm内的估计精度，满足NRTK的大气改正需求。

由表1、表2、图 6、图7可知，Kriging插值法相对于传统常用的内插算法有一定优势：在电离层估计方面，Kriging插值法与3种内插算法估计精度相当；对流层估计方面，Kriging插值法的精度要好于其他3种内插算法，特别是流动站位于网外的情况，LCM、LSM的估计精度都在dm级，而Kriging插值法仍能保持在cm级，好于其他2种算法。

4结束语

Kriging插值法虽然最初是基于地质学提出的，但是由于其能有效反应介质的空间相关性这一特性，将其引入NRTK中是可行的。实验证明；Kriging插值法对大气延迟的估计精度总体好于常规内插算法；特别是对流层估计方面，Kriging插值法相对于传统内插算法具有一定优势，不论流动站位于网外还是网内，插值精度都高于传统算法。需要指出的是：Kriging插值法虽然精度好于常规内插算法，但是其数据处理量大大超过常规算法，是以处理时间换取了精度；如何减少Kriging插值法的反应时间和提高其数据处理的效率值得进一步研究。

参考文献

[1]黄丁发，李成钢，吴耀强，等.GPS/VRS实时网络改正数生成算法研究[J].测绘学报，2007，36(3)：256-261.

[2]RIZOS C，HAN S.Reference station network based RTK systems：concepts & progress[J].Wuhan University Journal of Nature Sciences，2003，8(2B)：566-574.

[3]谢建涛.VRS改正数算法及精度分析[D].郑州：信息工程大学，2013：10-14.

[4]缪祥柱，施昆，沛捷，等.基于多基站网络的VRS差分信息的方法分析[J].测绘工程，2008，17(6)：29-36.

[5]黄丁发，周乐韬，李成钢，等.GPS增强参考站网络理论[M].北京：科学出版社，2011：12-13.

[6]李成钢，黄丁发，袁林果，等.GPS/VRS参考站网络对流层误差建模技术研究[J].测绘科学，2007，32(4)：29-31.

[7]DAI Liwen,HAN Shaowei,WANG Jinling,et al.Comparison of interpolation algorithms in network-based GPS techniques[J].The Journal of Navigation, 2003, 50(4):277-293.

[8]HAO Zhang.Optimal interpolation and the appropriateness of cross-validating variogram in spatial generalized linear mixed models[J].The Journal of Computation and Graphical Statistics，2003，12(3)：698-713.

[9]BLANCH J.An ionosphere estimation algorithm for WAAS based on kriging[C]//The Institute of Navigation(ION).Proceedings of the 15thInternational Technical Meeting of The Satellite Division of the Institution of Navigation.Manassas.VA：ION，2002：816-823.

[10]ALI A S，SUMSUNG L，RIZOS C.Functional models of ordinary kriging for real-time kinematic positioning based on the virtual reference station technique[C]// The Institute of Navigation(ION).Proceedings of the 23rd International Technical Meeting of the Satellite Division of The Institute of Navigation.Manassas.VA：ION，2010：2513-2521.

[11]毛田，万卫星，孙凌峰.用Kriging方法构建中纬度区域电离层TEC地图[J].空间科学学报，2007，27(4)：279-285.

[12]杨聪.GPS虚拟参考站算法研究及软件开发[D].北京：清华大学，2009：66-67.

[13]王家华，高海余，周叶.克里金地质绘图技术—计算机的模型和算法[M].北京：石油工业出版社，1990：150-154.

[14]WIELGOSZ，GREJNER B D，ALI A S.Regional ionosphere mapping with Kriging and multiquadric methods[J].Journal of Global Positioning Systems，2003，2(1)：48-55.

[15]翟进乾.克里金(Kriging)插值方法在煤层分布检测中的应用研究[D].太原：太原理工大学，2008：30-37.

[16]颜慧敏.空间插值技术的开发与实现[D].成都：西南石油学院，2005：14-17.

Errors correction of NRTK based on Kriging interpolation method

SHI Xin1，LV Zhiwei1，YANG Chuan2，ZHANG Yu1

(1.College of Navigation and Space Target Engineering，Information Engineering University，Zhengzhou 450001，China；2.Southwest Geotechnical Institute of China Nuclear Industry，Chengdu 610061，China)

Abstract：The paper used Kriging interpolation method to correct errors of rover to solve the problem that traditional interpolation method can’t correct well in network RTK，and explained the method with it’s mathematical principle.The results showed that Kriging interpolation method could correct user’s ionosphere delay and troposphere delay effectively and get higher accuracy than traditional interpolation method;the precision of ionosphere and tropospheric correction would have no obvious improvement while the user is inside of the stations net;and the Kriging interpolation method could correct atmospheric delay effectively even users locate a certain range outside of the stations net comparing with traditional interpolation method.

Keywords：Kriging；network RTK；ionosphere delay；troposphere delay；error correction

收稿日期：2015-09-11

基金项目：上海海事局项目(2013404705)；浙江北斗高精度地基增强网建设项目(AB14002006-4)。

第一作者简介：石鑫(1990—)，男，四川成都人，硕士研究生，研究反向为NRTK相关算法。

中图分类号：P228.1

文献标志码：A

文章编号：2095-4999(2016)02-0102-06

引文格式：石鑫，吕志伟，杨川，等.基于克里金插值法的NRTK误差改正[J].导航定位学报，2016，4(2)：102-107.(SHIXin，LVZhiwei，YANGChuan，etal.ErrorscorrectionofNRTKbasedonKriginginterpolationmethod[J].JournalofNavigationandPositioning，2016，4(2)：102-107.)DOI：10.16547/j.cnki.10-1096.20160222.